Fib-矩阵快速幂

大致四种情况：

A：1 1 平方2 1 三次3 2 

      1 0        1 1        2 1

poj3070：

即求A的n次方，最后输出【0】【1】；

---

原理

      n个初设小矩阵相乘， 则新得到的矩阵含有Fn ，Fn+1

                可 n 个小矩阵  太多了  ----->    

 

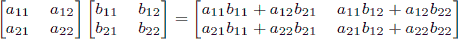    通过这个方法  升级，可以提升计算效率 O（log n  以二

为底）

---

解法二：打表

for(i = 1 ; i<=30 ;i++){
    a[1]=  (fabc[i-1][1]*fabc[i-1][1] + fabc[i-1][2]*fabc[i-1][3])%10000;
    a[2]=  (fabc[i-1][1]*fabc[i-1][2] + fabc[i-1][2]*fabc[i-1][4])%10000;
    a[3]=  (fabc[i-1][3]*fabc[i-1][1] + fabc[i-1][4]*fabc[i-1][3])%10000;
    a[4]=  (fabc[i-1][3]*fabc[i-1][2] + fabc[i-1][4]*fabc[i-1][4])%10000;
    
    fabc[i][1] = a[1];   
/*
一定注意上面的运算 要有个变量代替保存运算结果 ，
fabc 不能直接参与结果的赋值，否者上面的结果一定乱了，
想想看，WA的是不是这里
*/
    fabc[i][2] = a[2];
    fabc[i][3] = a[3];
    fabc[i][4] = a[4];
 
}

ac：这样就可以利用打好的表 进行任何数的运算了，注意 数的奇偶。

#include<stdio.h>
int fabc[30][5];
int s[5];
int a[5];
int solve( int l , int h ) {
	int i,k=0,c;
	while(1) {
		for( i = 0; 1<<i  <= h; i++);
		i--;
		a[1] = (s[1]*fabc[i][1] + s[2]*fabc[i][3])%10000;
		a[2] = (s[1]*fabc[i][2] + s[2]*fabc[i][4])%10000;
		a[3] = (s[3]*fabc[i][1] + s[4]*fabc[i][3])%10000;
		a[4]=  (s[3]*fabc[i][2] + s[4]*fabc[i][4])%10000;
		s[1] =a[1];
		s[2] = a[2];
		s[3] =a[3];
		s[4] = a[4];
		c = 1<<i;
		h = h- c;
		/*举个例子： h开始传过来的是10 ，表上的都是2的i次相乘，则循环第一次 
		去fabc[3][] 代表已经有(2^3)8个初始小矩阵相乘，
		还有两个没乘，h = 2进入下次循环，取表fabc[1][] (2^1), h = 0 退
		出 为偶数，最后输出偶数的输出形式即可
		*/ 
		if(h == 1)return 1;
		else if(h == 0) return 0;
	}
}
int main() {
	int n,i;
	fabc[0][4] = 0;
	fabc[0][1] = 1;
	fabc[0][2] = 1;
	fabc[0][3] = 1;
	
	for(i = 1 ; i<=30 ; i++) { //打表
		a[1]=  (fabc[i-1][1]*fabc[i-1][1] + fabc[i-1][2]*fabc[i-1][3])%10000;
		a[2]=  (fabc[i-1][1]*fabc[i-1][2] + fabc[i-1][2]*fabc[i-1][4])%10000;
		a[3]=  (fabc[i-1][3]*fabc[i-1][1] + fabc[i-1][4]*fabc[i-1][3])%10000;
		a[4]=  (fabc[i-1][3]*fabc[i-1][2] + fabc[i-1][4]*fabc[i-1][4])%10000;

		fabc[i][1] = a[1];
		fabc[i][2] = a[2];
		fabc[i][3] = a[3];
		fabc[i][4] = a[4];
	}
	while(scanf("%d",&n)) {
		if(n ==-1)break;
		s[1]= s[4] = 1;
		s[2]= s[3] = 0;
		if(solve(0,n))printf("%d\n",s[1]);   //基数
		else printf("%d\n",s[2]);   //偶数
	}
	return 0;
}

https://blog.csdn.net/ccf15068475758/article/details/52846726 

https://www.cnblogs.com/Konjakmoyu/p/4821044.html

随便看看