电力系统暂态稳定分析及报告：基于改进欧拉法与ode45求解器的matlab程序，基于Matlab的三机九节点电力系统暂态稳定分析及报告（24页）

电力系统暂态稳定程序以及报告（24页）
1.matlab暂态稳定分析程序，三机九节点系统，发电机模型采用经典二阶模型，负荷用恒阻抗模型，用改进欧拉法和matlab自带求解器ode45进行时域分析，实现微分方程和代数方程交替求解
2.模拟三相对称故障，进行暂态时域分析，分析暂态过程功角曲线
3.考虑了发电机的阻尼绕组的阻尼作用
4.可以考虑分析临界切除时间
5.适用于任何节点系统的简化暂态稳定分析
可

ID:33300754167603062

办法总比困难多

电力系统暂态稳定分析程序及报告

概述
电力系统暂态稳定是指在电力系统发生故障或负荷突变时，系统恢复稳态的过程。为了对电力系统的暂态稳定进行可靠分析，我们设计了一套基于Matlab的暂态稳定分析程序。该程序采用了三机九节点系统，并使用经典二阶模型表示发电机和恒阻抗模型表示负荷，通过改进欧拉法和Matlab自带求解器ode45进行时域分析，实现了微分方程和代数方程的交替求解。

程序结构
我们的程序主要分为以下几个部分：发电机模型、负荷模型、求解算法和结果分析。

1. 发电机模型
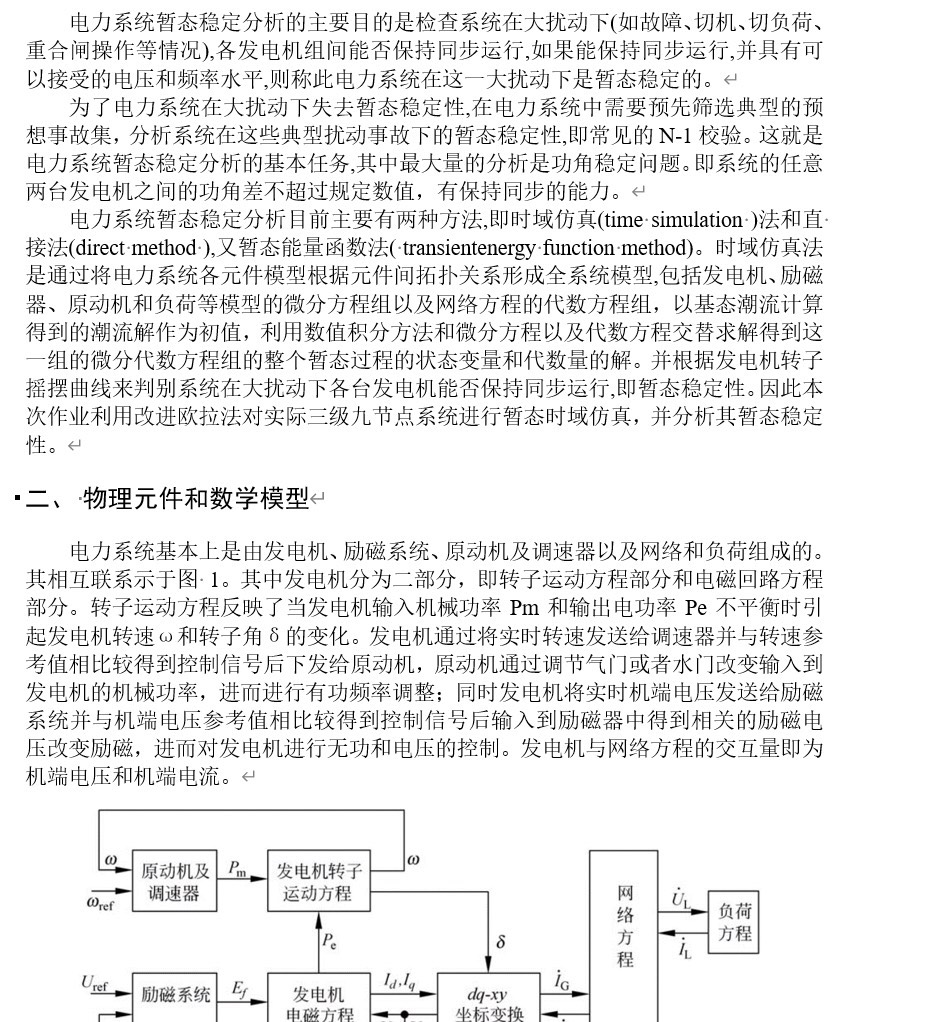
   我们采用经典的二阶模型表示发电机，该模型考虑了发电机的机械转动惯量、电磁转动惯量、励磁系统动态特性等因素。通过对发电机的模型建立，我们可以分析发电机在暂态过程中的功角变化情况，从而判断系统是否稳定。

2. 负荷模型
   为了简化问题，我们采用恒阻抗模型表示负荷。该模型假设负荷的电压和电流之间存在线性关系，并且负荷本身不参与暂态过程中的能量交换。通过对负荷的模型建立，我们可以分析负荷对系统暂态稳定性的影响。

3. 求解算法
   为了进行时域分析，我们采用改进的欧拉法和Matlab自带的求解器ode45进行微分方程和代数方程的交替求解。改进的欧拉法可以提高数值计算的精度，而ode45求解器则可以自动调整步长，保证求解过程的稳定性和准确性。

4. 结果分析
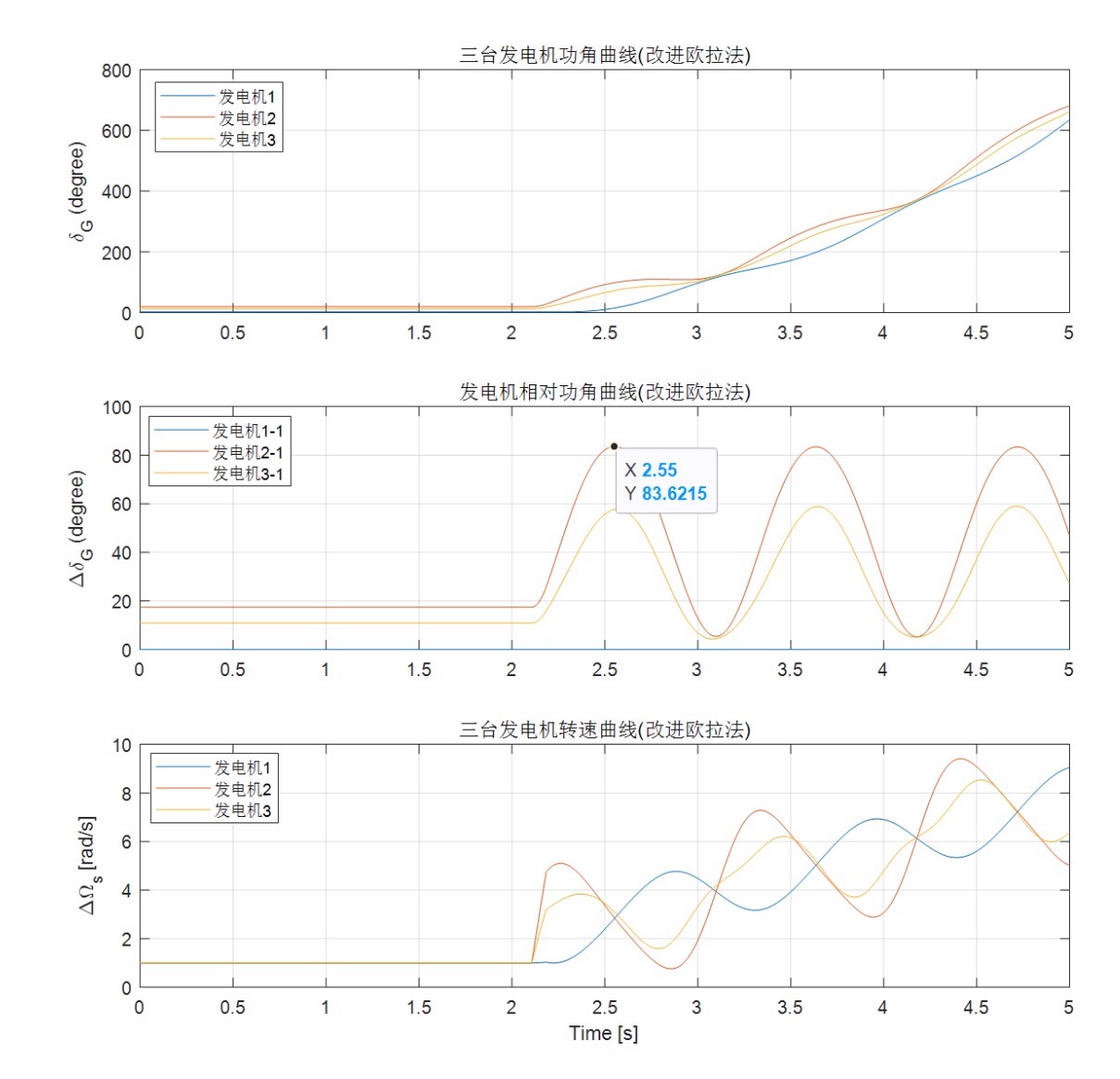
   通过我们的程序，可以模拟三相对称故障情况下的暂态过程，并绘制功角曲线。功角曲线可以反映系统暂态过程中发电机的功角变化情况，进而判断系统的稳定性。此外，我们还考虑了发电机的阻尼绕组对系统稳定性的影响，并可以分析临界切除时间，帮助工程师更好地设计和优化电力系统。

总结
我们设计的电力系统暂态稳定分析程序是一种简化而强大的工具，适用于任何节点系统的暂态稳定分析。通过该程序，工程师可以更好地分析电力系统在暂态过程中的稳定性，并进行相应的优化措施。未来，我们将继续完善该程序，提高其计算效率和准确性，为电力系统的稳定性分析提供更好的支持。

在程序员社区的博客上分享这篇技术文章，将会为读者提供一种新的思路和工具，帮助他们更好地理解和应用电力系统暂态稳定分析。

以上相关代码,程序地址：http://fansik.cn/754167603062.html