深度学习：softmax函数-CSDN博客

本文链接：https://blog.csdn.net/paipaixingong/article/details/122656112

本文详细介绍了回归问题中使用的恒等函数，二元分类问题中的sigmoid函数，以及多元分类问题中的softmax函数。特别针对softmax函数，提供了Python实现代码，并讨论了如何避免计算过程中出现溢出的问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一般回归问题的激活函数用的是恒等函数，二元分类问题用的是sigmoid函数，而多元分类问题可以使用softmax函数作为激活函数。

softmax函数式为：

softamx函数用Python实现：

import numpy as np
a = np.array([0.3,2.9,4.0])
exp_a = np.exp(a)
print(exp_a)
sum_exp_a = np.sum(exp_a)
print(sum_exp_a)
y = exp_a / sum_exp_a
print(y)

打印结果：

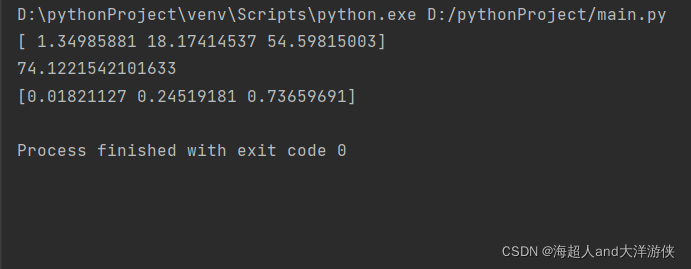
实际上为了防止计算溢出，也可以对softmax函数进行改进。

C'可以用任何值来代替，但是为了防止溢出，一般会使用输入信号中的最大值。

import numpy as np

def softmax(a):
    exp_a = np.exp(a)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    return y
a = np.array([1010,1000,990])
y = softmax(a)
print(y)

上述例子的结果会出现

[nan nan nan]

nan（not a number）

但是改进后的softmax函数则会计算出其正确的值

import numpy as np

def softmax(a):
    c = np.max(a)
    exp_a = np.exp(a - c)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    return y
a = np.array([1010,1000,990])
y = softmax(a)
print(y)

结果为：

[9.99954600e-01 4.53978686e-05 2.06106005e-09]

softmax函数的特征：

1、softmax输出的值是0.0到1.0之间的实数。并且，softmax函数的输出值的和是1。输出综合是1是softmax函数的一个重要性质。正因为这个性质，我们才可以把softmax函数的输出解释为“概率”。