一看到标题可能就郁闷了,什么是KD-tree,什么是KNN。没关系我会一一解释,生成DEM这个程序我写了好久也主要在完成KNN这个算法。
不过,首先用ArcGIS看一下我们数据点的分布(图1)以及最终生成的DEM(图2)。
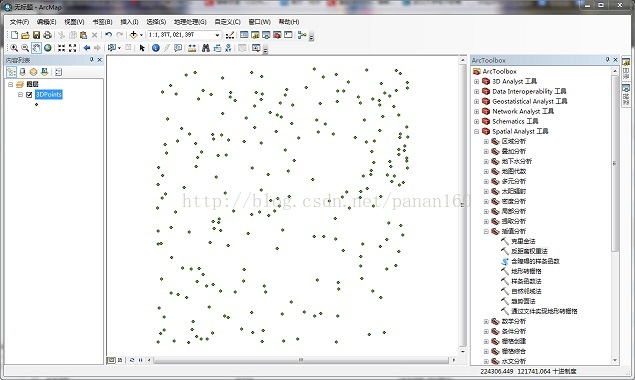
图1 原始数据点(229条数据)
图2 反距离权重法生成的DEM
反距离权重插值方法是一种局部插值方法,它假设未知值的点受较近控制点的影响比较远控制点的影响更大。这种方法通常用在计算机辅助制图方面。影响的程度(权重)用点之间距离乘方的倒数表示。乘方为1.0意味着点之间数值变化率为恒定,该方法称为线性插值法。乘方为2.0或更高意味着越靠近已知点数值的变化率越大,远离已知点趋于平滑。反距离权重法的通用方程如下:
式中, 为点0的估计值, 为控制点i的z值, 为控制点i与点0间的距离,s为在估算中用到的控制点数目,K为制定的幂。
可以看到,插值的原理很简单,下面我就开始进入代码部分了。
环境:VS2010 MFC
1、 遍历所有数据点得到坐标范围,建立MFC中View视图与原始数据的投影关系
这一点很重要,原始数据的坐标点为(222364.288,120033.674,56.796),而我们的View视图充其量也就是1000*800的大小,显然不经过坐标变换就不可能通过OnDraw()函数绘制出数据点。
坐标变换其次方程:
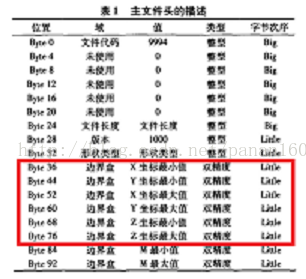
额外说明一点,坐标变换是所有GIS操作的前提,在.shp文件的文件头描述信息中同样包含数据范围信息。
2、 KNN
K最近邻(kNN,k-NearestNeighbor)是机器学习中的分类算法,所谓K最近邻,就是k个最近的邻居的意思,说的是每个样本都可以用她最接近的k个邻居来代表。
该方法的思路是:如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。KNN算法中,所选择的邻居都是已经正确分类的对象。
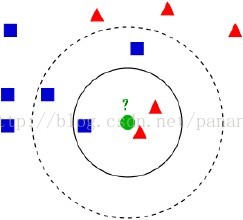
图3 kNN
图中如果K取3那么绿色圆点就会被归入三角形一类,如果取K=5,那么绿色圆点就会归入正方形类。
3、 KD-tree
把数据读入内存后我们就要开始插值工作了,为了提高对插值点邻近数据点的检索速率我们构造KD-tree对原始数据进行组织。
简介:
k-d树(k-dimensional树的简称),是一种分割k维数据空间的数据结构。主要应用于多维空间关键数据的搜索(如:范围搜索和最近邻搜索)。
k-d树是每个节点都为k维点的二叉树。所有非叶子节点可以视作用一个超平面把空间分区成两部分。在超平面左边的点代表节点的左子树,在超平面右边的点代表节点的右子树。超平面的方向可以用下述方法来选择:每个节点都与k维中垂直于超平面的那一维有关。因此,如果选择按照x轴划分,所有x值小于指定值的节点都会出现在左子树,所有x值大于指定值的节点都会出现在右子树。这样,超平面可以用该x值来确定,其法矢为x轴的单位矢量。
如图:
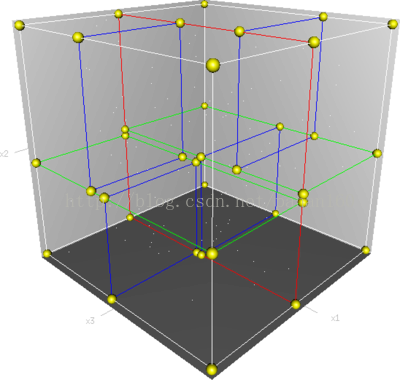
图4 三维k-d树的划分
图中,一个三维k-d树。第一次划分(红色)把根节点(白色)划分成两个节点,然后它们分别再次被划分(绿色)为两个子节点。最后这四个子节点的每一个都被划分(蓝色)为两个子节点。因为没有更进一步的划分,最后得到的八个节点称为叶子节点。
再举一个二维数据的例子(很多博客写的不错,我直接搬过来):
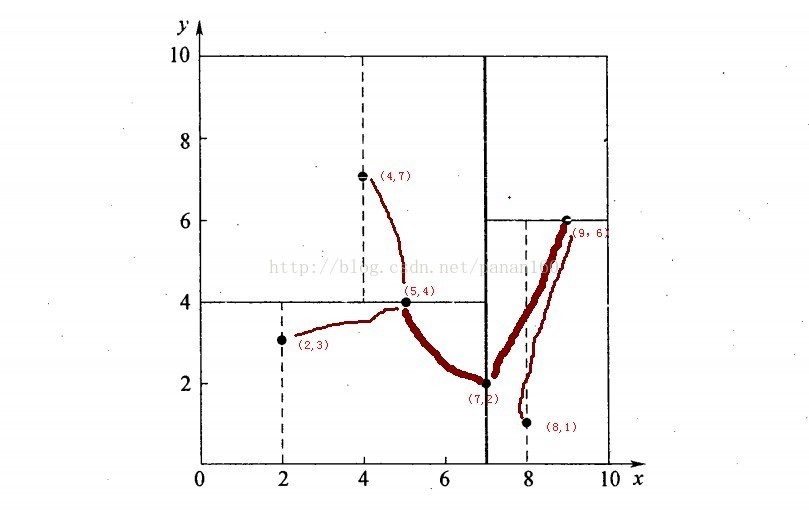
假设有6个二维数据点{(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)},数据点位于二维空间内,如下图所示。为了能有效的找到最近邻,k-d树采用分而治之的思想,即将整个空间划分为几个小部分,首先,粗黑线将空间一分为二,然后在两个子空间中,细黑直线又将整个空间划分为四部分,最后虚黑直线将这四部分进一步划分(图5)。
图5 二维k-d树的构造
6个二维数据点{(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)}构建kd树的具体步骤为:
Ø 确定:split域=x。具体是:6个数据点在x,y维度上的数据方差分别为39,28.63,所以在x轴上方差更大,故split域值为x;
Ø 确定:Node-data=(7,2)。具体是:根据x维上的值将数据排序,6个数据的中值(所谓中值,即中间大小的值)为7,所以Node-data域位数据点(7,2)。这样,该节点的分割超平面就是通过(7,2)并垂直于:split=x轴的直线x=7;
Ø 确定:左子空间和右子空间。具体是:分割超平面x=7将整个空间分为两部分:x<=7的部分为左子空间,包含3个节点={(2,3),(5,4),(4,7)};另一部分为右子空间,包含2个节点={(9,6),(8,1)};
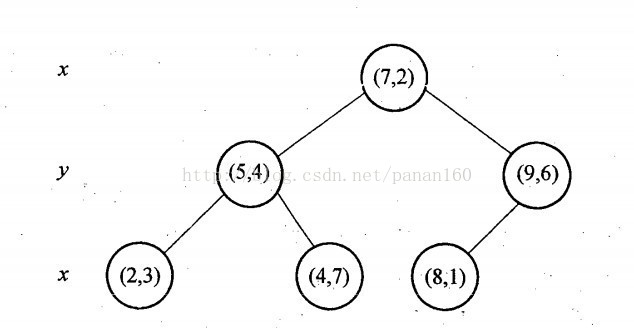
与此同时,经过对上面所示的空间划分之后,我们可以看出,点(7,2)可以为根结点,从根结点出发的两条红粗斜线指向的(5,4)和(9,6)则为根结点的左右子结点,而(2,3),(4,7)则为(5,4)的左右孩子(通过两条细红斜线相连),最后,(8,1)为(9,6)的左孩子(通过细红斜线相连)。如此,便形成了下面这样一棵k-d树:
图6 二维kd-tree的树形结构
KD-tree的数据结构:
/** a node in a k-d tree */
struct kd_node
{
int ki; /**< partition key index */
double kv; /**< partition key value */
int leaf; /**< 1 if node is a leaf, 0 otherwise */
struct feature* features; /**< features at this node */
int n; /**< number of features */
struct kd_node* kd_left; /**< left child */
struct kd_node* kd_right; /**< right child */
};
经过上面的解释这个数据结构应该很好理解了。
KD-tree查询:
我懒得写了,看这里吧
http://www.cnblogs.com/eyeszjwang/articles/2429382.html
4、 KD-tree算法的C实现
(以下代码改自Rob Hess维护的sift库:http://blogs.oregonstate.edu/hess/code/sift/;关于什么是sift我就不再解释了,有兴趣的自己去了解)
简单的说一下sift算法中要完成对128维向量的K邻近搜索,这里我们只需将128维的邻近搜索简化到2维空间即可。算法的代码实现与伪码还是有一些区别,这里我将重点介绍,同时把涉及的几个排序算法也简单介绍下。
节点数据结构:
struct points
{
double pointX;
double pointY;
double pointZ;
void * feature_data;
};
struct kd_node2
{
bool ki; /**< partition key index true=x false=y*/
double kv; /**< partition key value */
int leaf; /**< 1 if node is a leaf, 0 otherwise */
struct points* m_points;
int n; /**< number of points */
struct kd_node2* kd_left; /**< left child */
struct kd_node2* kd_right; /**< right child */
};
核心函数如下:
/**
* @brief 构建KD-tree的入口函数
* @param1 待插入的数据点数组
* @param2 数据点个数
* @return 返回KD-tree的根节点
*/
struct kd_node2* kdtree_build( struct points* m_points, int n )
{
struct kd_node2* kd_root;
if( ! m_points || n <= 0 )
{
fprintf( stderr, "Warning: kdtree_build(): no features, %s, line %d\n",
__FILE__, __LINE__ );
return NULL;
}
kd_root = kd_node2_init( m_points, n ); // 分配空间 [8/4/2014 pan]
kd_root->ki=true; // 指定第一次分隔方向为X [8/4/2014 pan]
<span style="color:#cc0000;">expand_kd_node2_subtree( kd_root );</span>
return kd_root;
}
/**
* @brief 展开子树
* @param1 子树的父节点
* @return null
*/
static void expand_kd_node2_subtree( struct kd_node2* kd_node2 )
{
/* base case: leaf node */
if( kd_node2->n == 1 || kd_node2->n == 0 ){
kd_node2->leaf = 1;
return;
}
assign_part_key( kd_node2 ); // 加入新参数 表示分隔方向!!! [8/4/2014 pan]
partition_features( kd_node2 );
if( kd_node2->kd_left )
<span style="color:#cc0000;">expand_kd_node2_subtree( kd_node2->kd_left );</span>
if( kd_node2->kd_right )
<span style="color:#cc0000;">expand_kd_node2_subtree( kd_node2->kd_right );</span>
}
从红色部分的代码,我们可以看出kd-tree树的构造过程利用了递归,分而治之的方法。
/**
* @brief 计算分隔值kv
* @param1 当前kd-tree节点
* @return null
*/
static void assign_part_key( struct kd_node2* kd_node2 )
{
struct points* m_points;
double kv, x, mean, var, var_max = 0;
m_points = kd_node2->m_points; // 得到指向特征点的指针 [8/3/2014 pan]
int n = kd_node2->n; // 得到特征点的个数 [8/3/2014 pan]
double *tmp =(double*) calloc( n, sizeof( double ) );
if(kd_node2->ki){ //Kd-tree X 方向分隔
for(int i=0;i<n;i++){
tmp[i]=m_points[i].pointX;
}
}
else{ //Kd-tree Y 方向分隔
for(int i=0;i<n;i++){
tmp[i]=m_points[i].pointY;
}
}
<span style="color:#cc0000;">kv = median_select( tmp, n );</span> // 寻找中值 [8/3/2014 pan]
free( tmp );
kd_node2->kv = kv;
}
Sift代码中的这部分是通过计算数据方差决定数据划分的方式,这里做出简化,采用x,y交替的方式划分数据。关于中值的计算kv = median_select( tmp, n ),使用的是插入排序的算法,一会在进行介绍。
/*
Partitions the features at a specified kd tree node to create its two
children.
@param kd_node2 a kd tree node whose partition key is set
*/
static void partition_features( struct kd_node2* kd_node2 )
{
struct points* m_points, tmp;
double kv;
int n, p, i, j = -1;
m_points = kd_node2->m_points;
n = kd_node2->n;
bool ki = kd_node2->ki;
kv = kd_node2->kv; // 分割值 [8/3/2014 pan]
/******以下for循环完成这样的功能:
/* 把小于分割节点的features放到了【0,j】区间,
/* j为分割节点,
/* 【j,n】为大于分割节点的features [8/3/2014 pan]******/
for( i = 0; i < n; i++ ){
if(ki){ //X 方向分隔
if(m_points[i].pointX <= kv ){
tmp = m_points[++j];
m_points[j] = m_points[i];
m_points[i] = tmp;
if( m_points[j].pointX == kv ){ // 此行代码必定会执行到,因为kv是这些数值的中值 [8/3/2014 pan]
p = j;
}
}
}
else{
<span style="color:#cc0000;">if(m_points[i].pointY <= kv ){
tmp = m_points[++j];
m_points[j] = m_points[i];
m_points[i] = tmp;
if( m_points[j].pointY == kv ){ // 此行代码必定会执行到,因为kv是这些数值的中值 [8/3/2014 pan]
p = j;
}
}
}</span>
}
tmp = m_points[p];
m_points[p] = m_points[j];
m_points[j] = tmp;
/* if all records fall on same side of partition, make node a leaf */
if( j == n - 1 ){
kd_node2->leaf = 1;
return;
}
ki=!ki; // 代替ki的计算过程,X、Y交替作为数据封方向 [8/10/2014 pan]
kd_node2->kd_left = kd_node2_init( m_points, j + 1 );
kd_node2->kd_left->ki=ki;
kd_node2->kd_right = kd_node2_init( m_points + ( j + 1 ), ( n - j - 1 ) );
kd_node2->kd_right->ki=ki;
}
以上代码是构建KD-tree最核心的部分,简单来说,每一次递归使用快速排序算法的一步,完成了对本结点(kd_node)所有的数据点的一个排序,再分别将本结点的左树即右树进行展开。
注意:每一次递归并没有形成严格递增递减的排序队列
熟悉算法的同学看到上面红色部分的代码就应该能立即反应出来这是一个快排,那么不知道这个算法的也没关系,举个例子解释一下每次递归时在这里发生了什么,同时也验证一下最终生成的KD-tree是什么样子。
测试数据:(50,50,1)、(40,60,2)、(60,40,3)、(20,20,4)、(30,70,5)、(60,50,6)、(70,10,7)
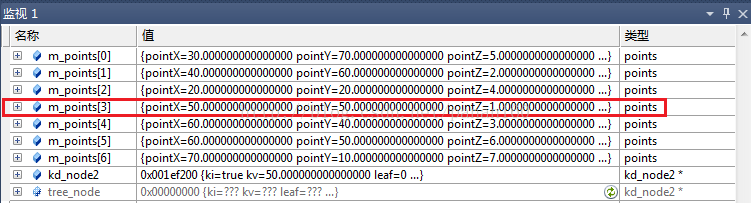
进入partition_features()函数后数据的初始状态(分隔方向x,分隔值kv=50):
图7 数据初始值
经过一次迭代后,此时可以发现数组依据pointX值分成了两部分。pointX值小于kv的排在前面,大于kv的排在后面。这就是一个典型的快排过程。
图8 第一次迭代
第二次迭代,进入上一节点的左子数,分隔方向y,分隔值kv=50。注意此时n=4,也就是只排列前4个数据点。经过第二次迭代后,前4个数据点依据pointY分成了下于kv大于kv的两部分。
图9 左子树迭代
第三次迭代,第四次迭代……不再一一介绍
图10 最终结果
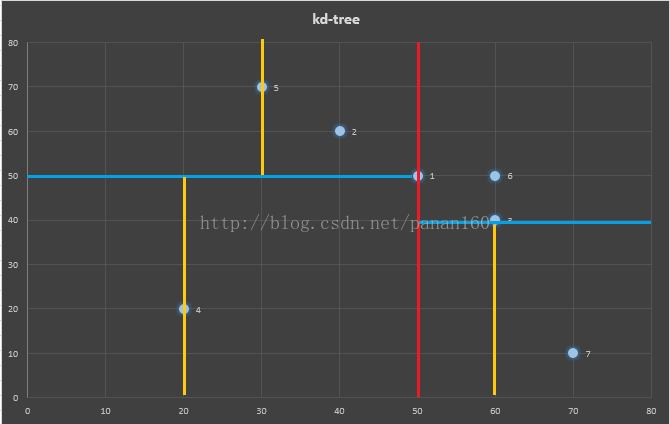
最终7个点的区域划分及建立的KD-tree如下所示:
图11 测试数据的kd-tree二维划分
图12 测试数据的树形结构
二叉树的顺序存储结构就是用一维数组存储二叉树中的各个节点,并且节点的存储位置能体现结点之间的逻辑关系
5、 堆排序、插入排序、快速排序
排序就是排大小么,干嘛用三种不同的算法,搞这么复杂?答案是这些排序算法的确各有千秋。
5.1 堆排序
堆排序的时间复杂度是 ,堆排序具有空间原址性:任何时候都只需要常数个额外的元素空间存储临时数据。
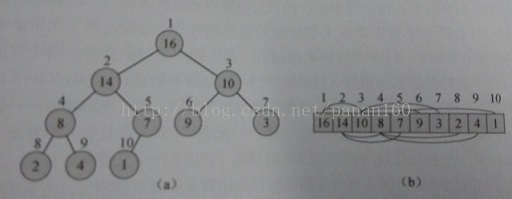
堆:是一个数组,它可以被看出一个近似的完全二叉树,树上的每一个节点对应数组中的一个元素。除了底层外,该树是完全充满的。一个典型的对结构如下:
二叉堆可以分成两种形式:最大堆和最小堆。在这两种堆中,节点的值都要满足堆的性质。最大堆中,最大堆的性质是指除了根以外的所有节点 都要满足: ;与此相反最小堆应满足: 。
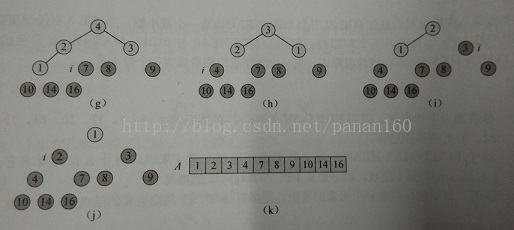
堆排序:在进行堆排序的时候我们首先将输入数组 构建成最大堆。因为数组中最大的元素总在根节点 中,通过把它与 进行互换,我们可以让该元素放到正确的位置。由于这一调整可能会影响最大堆的性质,因此我们需要对数组 进行堆调整,使其满足最大堆的性质,进而重复第一步。其过程可以图表示:
5.2 插入排序
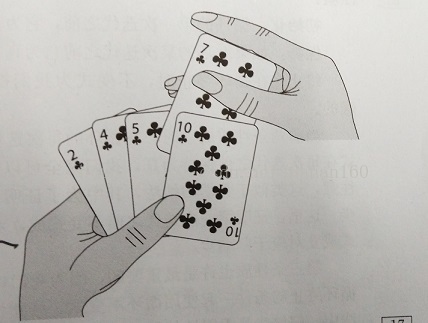
对于少量数据元素,插入排序是一个有效的算法。插入排序的工作方式像许多人排序一手扑克牌。开始时,我们的左手为空并且桌子上的牌面向下。然后,我们依次从桌子上拿走一张牌并将它插入到左手正确的位置。为了只找到一张牌的正确位置,我们从右到左将它与已转载手中的每张牌进行比较,原来这些牌是桌子上牌堆顶部的牌。
5.3 快速排序
快速排序是一种最坏情况时间复杂度为 的排序算法。虽然最坏情况时间复杂度差,但是快速排序的平均性能非常好,它的期望时间复杂度是 ,此外它还能够进行原址排序。
快速排序也使用了分治思想。一个典型的子数组 进行快速排序的三步分治过程:
分解:数组 被划分为两个(可能为空)子数组 和 ,使得 中的每一个元素都小于等于 ,而 也小于等于 中的每个元素。其中,计算下标 也是划分过程的一部分。
解决:通过递归调用快速排序,对子数组 和 进行排序。
合并:因为子数组都是原址排序的,所以不需要进行合并操作,数组 已经有序。5.4 总结
这些排序算法中插入排序是最简单的,代码也是最少的,因此运用在了原始数据排序找中值kv的过程。当然也使用了一个小技巧,就是将原始数据每5个一组,利用插入排序寻找5个数据的中值,最后再找到所有数据的中值。快速排序中将数组划分为两部分的过程与KD-tree的建立过程十分相似,因此KD-tree的建立整体上是对快速排序中“分解”多次迭代的过程。注意到图8快速排序的过程中元素的移动是非常有限的,一次“分解”过程只需要一半左右的元素进行位置交换。同时快速排序是原址排序,这样就减少了程序的空间复杂度。最后堆排序实际上主要是为了利用最小堆的性质,利用最小堆建立优先队列进而完成K邻近的搜索。6、 程序运行结果
最后的最后,把生成的DEM效果图贴出来,对比一下和ArcGIS生成的区别不大,大功告成。










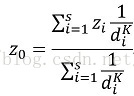




















 1105
1105

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








