小朋友们好,大朋友们好!
我是猫妹,一名爱上Python编程的小学生。
和猫妹学Python,一起趣味学编程。

今日主题
之前学过了图的基本概念和图的两种遍历算法
怎么样?
你学会了吗?
接下来,咱们学习下几种图的应用。
今天,咱们要学习的内容是:
什么是树
图的最小生成树算法
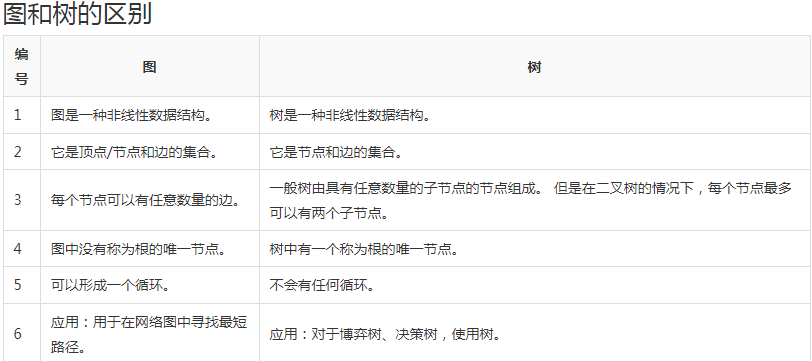
图和树
图,之前咱们已经学习过了。
在计算机中,什么是树呢?
树是图的子集,树是图,图不一定是树。
树是一种“层次”关系,图是“网络”关系。
树是一种特殊的图:
1. 一个无环的无向连通图,称之为树。
2. 由n个点、n-1条边组成的无向连通图,称之为树。
证明:
n个点要连通,至少需要n-1条边(无向边),而刚好n-1条边必然不能构成环(要构成环,至少有一个点的度数≥3),所以这是一棵树。

图可以有环,树没有环。
我们直观感受下:

图是两个集合 V 和 E 的集合,其中 V 是顶点的有限非空集,E 是边的有限非空集。
-
顶点只不过是图中的节点。
-
两个相邻的顶点由边连接。
-
任何图都表示为 G = {V, E}。
示例:G = {{V1, V2, V3, V4, V5, V6}, {E1, E2, E3, E4, E5, E6, E7}}

树是一个或多个节点的有限集合,使得:
-
有一个专门指定的节点,称为 root。
-
其余节点被划分为 n>=0 不相交集 T1, T2, T3, …, Tn
-
其中 T1, T2, T3, …, Tn 称为根的子树。
12


图的最小生成树算法
最小生成树算法是用来求解一个图的最小生成树的算法。
比如,下图中的图产生了两个数,下左的权重和是15,下右的权重和是16。
所谓图的最小生成树,就是找到一棵树,其权重和最小。

常用的最小生成树算法有 Kruskal 算法和 Prim 算法。
Kruskal 算法的思想,简单来说,就是如果一个图有 n 个顶点,选出总权值最小并且不会构成回路的 n-1 条边使得图中的任意两个顶点都能通过这 n-1 条边中的若干条边连通。
对于 Kruskal 算法的实现,既然要选择选择 n-1 条边并且边的总权值最小,那么我们可以先对这个图的所有边按权值进行从小到大排序,然后依次选择边。

Prim 算法是一种贪心算法,用于在加权连通图中找到其最小生成树。
具体来说,我们从一个未被包含在最小生成树中的点开始,每次选择距离该点最近的未被包含在最小生成树中的点,并将它们连接起来形成一条边。
这样一直进行下去,直到所有的点都被包含在最小生成树中为止。
Prim 算法实现


-
逻辑很简单,先选取一个起始节点,然后从其相邻的边种,选取权值最小的边进行连接。
-
将新连接后的节点和之前的节点一起,从这些节点中选取权值最小的边进行连接。
-
如此反复。知道所有的节点都被访问。
比如:
-
和0连接的边中,权值分别为{10、28},选取10。
-
加入节点5,和节点{0,5}相邻的边有{25,28},选取25。
-
如此反复。
从几个权值中,选取一个最小的。
这个要怎么实现呢?
可以用Python中的heapq实现。
heapq库提供了一些函数,如heappush、heappop、heappushpop等,用于操作堆。


代码实现(完整代码,见同名公众号,次条推文):

代码逻辑:
14行:s表示已经访问过的结点
15行:优先级队列,用于找一个最小权值
16行:res,实际生成的最小生成树路径
17行:边的数量比结点少一
18~19行:将当前结点相邻结点和权值放入队列
22行:从队列中选择一个权值最小的
23行:结点不能访问过,否则就不是树了
24行:保存当前结点
25行:保存当前路径
26行:更新当前结点
运行结果:


好了,我们今天就学到这里吧!
如果遇到什么问题,咱们多多交流,共同解决。
我是猫妹,咱们下次见!







 本文介绍了树的概念,作为图的一种特殊形式,强调树是没有环的无向连通图。接着,讲解了如何寻找图的最小生成树,提到了Kruskal和Prim两种算法,并用Python的heapq库展示了Prim算法的实现过程。
本文介绍了树的概念,作为图的一种特殊形式,强调树是没有环的无向连通图。接着,讲解了如何寻找图的最小生成树,提到了Kruskal和Prim两种算法,并用Python的heapq库展示了Prim算法的实现过程。
















 9900
9900

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








