最短路径算法----Floyd-warshall（十字交叉算法证明）

Floyd不同于Dijkstra，可以得到所有点对的最短路径。使用的是DP

Floyd可以处理有负权重边的情况

递推公式：w(i, j) = min{w(i, j), w(i, k) + w(k, j)}，含义是【i到j的最短距离】=【i到k的最短距离+k到j的最短距离】与【i到j的最短距离】中较小的那一个

看起来很简单，但是具体怎么计算呢？

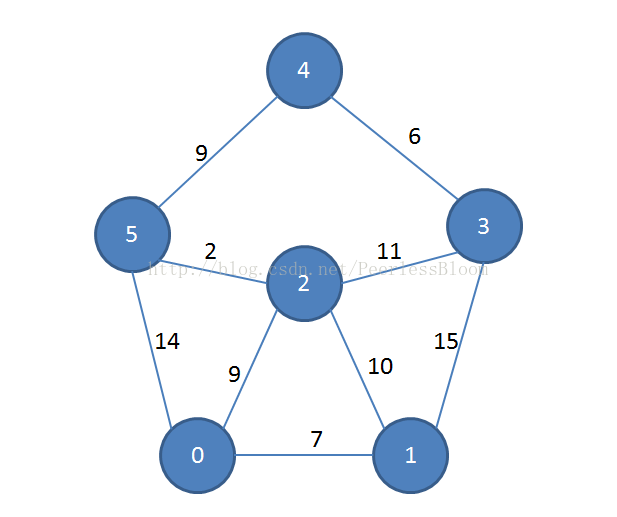
依旧使用这个例子，图的表示方式为：

[[0, 7, 9,  max,  max, 14],
 [7, 0, 10, 15, max, max],
 [9, 10, 0, 11, max, 2],
 [max, 1