根据卫星轨道参数（Two Line Element）模拟星下点轨迹

最方便获取的卫星轨道参数是北美防空司令部（NORAD）发布的两行根数（Two Line Element）

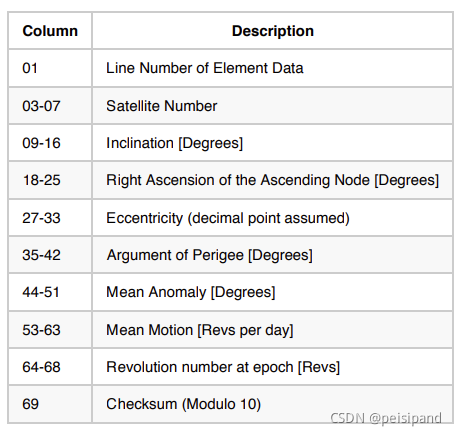
 主要根数记录在第二行：（inclination）轨道倾角，升交点经度，轨道偏心率，近地点角距，平近点角，（mean motion）平运动速率。

星下点轨迹绘制

以GAOFEN5参数为例，半长轴等于地球半径+轨道高度。

 

 

clc
close all
clear all
%%
W_EARTH =7.29e-5; %地球自转速度
GGC =3.986e5;%地球引力常数
%轨道六根数
a =(6371 + 705)*1e3; %地球半径
e =0.003123; %轨道偏心率
i =98.2358*pi/180; %轨道倾角
w =75.3926*pi/180; %轨道近地点幅角
RAAN =192.8991*pi/180; %升交点赤经

T = 2*pi*sqrt((a^3)/GGC);
N_T=fix(86400*0.2/T);%绘制近地轨道星下点，周期远小于24h   86400s=24h
%轨道真近点角计算
Ts= 5; %采样时间间隔 s
t =0:Ts:fix(N_T*T); %采样时间点
tp =0; 
n =sqrt(GGC/a^3); %卫星平运动时间
M =n*(t-tp);%星平近点角
f =M+(2*e-e^3/4)*sin(M)+1.25*e^2*sin(2*M)+13/12*e^3*sin(3*M);%轨道真近点角
%%
Rz_RAAN =[cos(RAAN) -sin(RAAN) 0;sin(RAAN) cos(RAAN) 0; 0 0 1];
Rz_w =[cos(w) -sin(w) 0;sin(w) cos(w) 0;0 0 1];
Rx_i =[1 0 0;0 cos(i) -sin(i);0 sin(i) cos(i)]; %坐标转换矩阵
R =a*(1-e^2)./(1+e*cos(f));%卫星距地心的距离，考虑f的离散值
r_sv =[R;R;R].*[cos(f);sin(f);zeros(1,size(f,2))];%卫星在轨道坐标系中的坐标
r_so =Rz_RAAN*Rx_i*Rz_w*r_sv;%卫星在地心惯性坐标系中的坐标
x_so =r_so(1,:);%卫星在地心惯性坐标系的分量
y_so =r_so(2,:);%卫星在地心惯性坐标系的分量
z_so =r_so(3,:);%卫星在地心惯性坐标系的分量
%卫星纬度delta,大于0为北纬
delta =atan(z_so./sqrt(x_so.^2+y_so.^2))*180/pi;
%卫星经度delta，大于180为西经
for m=1:1:size(r_so,2)
    if(r_so(1,m)<0)
        alpha(m) =180+atan(r_so(2,m)/r_so(1,m))*180/pi;
    else if (r_so(2,m)>0)
            alpha(m) =atan(r_so(2,m)/r_so(1,m))*180/pi;
         else
             alpha(m) =360+atan(r_so(2,m)/r_so(1,m))*180/pi;
        end
    end
      
end
%%
 figure(1)                           %out 
 axis([-180 180 -90 90]) 
 set(gcf,'outerposition', get(0,'screensize')); 
 geoshow('landareas.shp', 'FaceColor', [1 1 1]); 
 grid on 
 hold
alpha1 =rem((alpha-W_EARTH*t*180/pi+N_T*360),360);
for m=1:1:size(r_so,2)
if alpha1(m)>180
          alpha1(m)=alpha1(m)-360;
end;
% alpha1(m)=-alpha1(m);
end
plot(alpha1,delta,'.');
plot(115.25,39.26,'*')
grid;
xlabel('卫星经度');
ylabel('卫星纬度');
%%

matlab代码绘制的结果与在线绘制的相同。 

在线绘制星下点轨迹

北美防空司令部 Two-Line Element