T1:问题 A: 石子合并
题目描述
在一个圆形操场的四周摆放了n堆石子(n< 100),现要将石子有次序地合并成一堆。规定每次只能选相邻的两地合并成新的一堆， 并将新的一堆的石子数记为该次合并的得分。
编程,读入堆数n及每堆石子数(≤20),选择一种合并石子的方案,使得做n-1次合并,得分的总和最小;选择一种合并石子的方案，使得做n-1次合并,得分的总和最大。
例如，如图1所示的4堆石子,每堆石子数(从最上面的一堆开始按顺时针方向数)依次为4、5、9、4,则3次合并得分总和最小的方案如图2所示,得分总和最大的方案如图3所示。
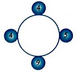
图1 样例所示的4堆石子
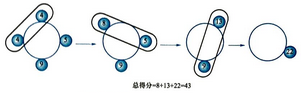
图2 样例所示得分总和最小的方案
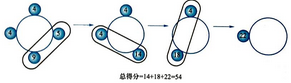
图3 样例所示得分总和最大的方案
输入
第1行为石子堆数,第2行为每堆石子数,每两个数之间用一个空格分隔。
输出
第1行为最小得分值,第2行为最大得分值。
样例输入
4
4 5 9 4
样例输出
43
54
题解
首先看看这道题是不是贪心。根据最初的想法，每次选取和最大或最小的石子进行合并。但是试过几组数据发现，这种贪心方式是错误的。因此我们来考虑dp。由于题目规定只能把相邻的两堆进行合并，因此很容易想到区间dp。但是由于这是一个环，因此先把环扩展为链，再进行区间处理。首先最外层肯定枚举区间长度，然后枚举左端点，自然右端点也就出来了。然后怎么转移呢，可以由两个小区间合并而来，所以第三维再枚举一个端点就行了注意是2个dp。
参考代码
#include<cstdio>
#include<cstring>
using namespace std;
int n,a[500],dp1[300][300],sum[500],dp2[300][300];
int max1(int p,int q) { return p>q?p:q; }
int min1(int p,int q) { return p<q?p:q; }
int main()
{
scanf("%d",&n);
memset(dp2,127/3,sizeof(dp2));
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
dp2[i][i]=dp2[i+n][i+n]=0;
a[i+n]=a[i];
}
for(int i=1;i<=n*2;i++) sum[i]=sum[i-1]+a[i];
for(int len=2;len<=n;len++)
{
for(int l=1;l+len-1<=n*2;l++)
{
int r=l+len-1;
for(int k=l;k<r;k++)
{
dp1[l][r]=max1(dp1[l][r],dp1[l][k]+dp1[k+1][r]+sum[r]-sum[l-1]);
dp2[l][r]=min1(dp2[l][r],dp2[l][k]+dp2[k+1][r]+sum[r]-sum[l-1]);
}
}
}
int minn=999999999;
for(int i=1;i<=n;i++)
if(dp2[i][i+n-1]<minn)
minn=dp2[i][i+n-1];
printf("%d\n",minn);
int maxn=-1;
for(int i=1;i<=n;i++)
if(dp1[i][i+n-1]>maxn)
maxn=dp1[i][i+n-1];
printf("%d",maxn);
return 0;
}T2：问题 B: 对抗赛
题目描述
程序设计对抗赛设有 N（0<N≤50 的整数）个价值互不相同的奖品，每个奖品的价值分别为 S1，S2，S3……Sn（均为不超过 100 的正整数）。现将它们分给甲乙两队，为了使得甲乙两队得到相同价值的奖品，必须将这 N 个奖品分成总价值相等的两组。
编程要求：对给定 N 及 N 个奖品的价值，求出将这 N 个奖品分成价值相等的两组，共有多少种分法？
例如：N = 5，S1，S2，S3……Sn 分别为 1，3，5，8，9
则可分为{1，3，9}与{5，8}
仅有 1 种分法；
例如：N = 7，S1，S2，S3……Sn 分别为 1，2，3，4，5，6，7
则可分为：
{1,6,7}与{2,3,4,5}
{2,5,7}与{1,3,4,6}
{3,4,7}与{1,2,5,6}
{1,2,4,7}与{3,5,6}
有4 种分法。
输入
第一行一个整数N；
第二行N个数据：S1，S2，S3……Sn，每两个相邻的数据之间有一个空格隔开。
输出
一行一个整数，表示多少种分法的答案，数据若无解，则输出 0。
样例输入
7
1 2 3 4 5 6 7
样例输出
4
题解
这道题是一道存在性背包的题，其一明显的性质就是价值和并不大。于是我们枚举每一个数，再枚举每一种可能的价值，用桶来存，于是经过一遍扫描后，就可以得到所有可能的和，然后再看是否有价值总和一半的情况，并直接输出个数即可。注意，我们所求的是所有答案是总和一半的组合情况，由于两种组合是一种分法，因此最后还要除以2才是答案。
参考代码
#include<cstdio>
using namespace std;
int n,a[500],dp[5001],s;
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
s+=a[i];
}
if(s%2==1)
{
printf("%d",0);
return 0;
}
dp[a[1]]++;
for(int i=2;i<=n;i++)
{
for(int j=s/2;j>=a[i];j--)
{
if(dp[j-a[i]])
{
dp[j]+=dp[j-a[i]];
}
}
dp[a[i]]++;
}
printf("%d",dp[s/2]/2);
return 0;
}T3:问题 C: 演讲大厅安排
题目描述
有一个演讲大厅需要我们管理，演讲者们事先定好了需要演讲的起始时间和中止时间。我们想让演讲大厅得到最大可能的使用。我们要接受一些预定而拒绝其他的预定，目标是使演讲者使用大厅的时间最长。假设在某一时刻一个演讲结束，另一个演讲就可以立即开始。
编程任务：
1、输入入演讲者的申请。
2、计算演讲大厅最大可能的使用时间。
3、输出结果。
输入
第一行为一个整数 N，N≤5000，表示申请的数目。
以下 n 行每行包含两个整数 p，k，1 ≤ p < k ≤ 30000，表示这个申请的起始时间和中止时间。
输出
一个整数，表示大厅最大可能的使用时间。
样例输入
12
1 2
3 5
0 4
6 8
7 13
4 6
9 10
9 12
11 14
15 19
14 16
18 20
样例输出
16
题解
这道题其实运用了贪心的思想，还是枚举每个时间段，只不过要想一个策略使该种贪心方法无后效性，即贪一个放一个。因此我们可以先左端点排序，在左端点相同时，再按照右端点排序，再枚举之前所有时间，看看有无冲突，没有就转移，因此我们还是要用到dp，只不过是在贪心的基础上完成的。这样做是O(n*n)的效率。那么有没有更好的方法呢？其实我们完全可以维护一个单调队列，每次二分查找第一个与之不冲突的时间，并且用sum数组来记录每一个单调队列中的最大值，这样配合二分就可以log地完成当前时间段的转移。此处给出第一种朴素的算法代码。
参考代码
#include<cstdio>
#include<algorithm>
using namespace std;
struct node
{
int l,r;
}a[12000];
int n,dp[6000],maxn=-1;
bool comp1(node p,node q)
{
return p.l<q.l || p.l==q.l && p.r<q.r;
}
int max1(int p,int q) { return p>q?p:q; }
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d%d",&a[i].l,&a[i].r);
sort(a+1,a+n+1,comp1);
dp[1]=a[1].r-a[1].l;
maxn=dp[1];
for(int i=2;i<=n;i++)
{
for(int j=1;j<i;j++)
{
if(a[i].l>=a[j].r)
dp[i]=max1(dp[i],dp[j]);
}
dp[i]+=a[i].r-a[i].l;
maxn=max1(maxn,dp[i]);
}
printf("%d",maxn);
return 0;
}T4:问题 D: 传纸条
题目描述
小渊和小轩是好朋友也是同班同学，他们在一起总有谈不完的话题。一次素质拓展活动中，班上同学安排做成一个 m 行 n 列的矩阵，而小渊和小轩被安排在矩阵对角线的两端，因此，他们就无法直接交谈了。幸运的是，他们可以通过传纸条来进行交流。纸条要经由许多同学传到对方手里，小渊坐在矩阵的左上角，坐标(1,1)，小轩坐在矩阵的右下角，坐标(m,n)。从小渊传到小轩的纸条只可以向下或者向右传递，从小轩传给小渊的纸条只可以向上或者向左传递。
在活动进行中，小渊希望给小轩传递一张纸条，同时希望小轩给他回复。班里每个同学都可以帮他们传递，但只会帮他们一次，也就是说如果此人在小渊递给小轩纸条的时候帮忙，那么在小轩递给小渊的时候就不会再帮忙。反之亦然。
还有一件事情需要注意，全班每个同学愿意帮忙的好感度有高有低（注意：小渊和小轩的好心程度没有定义，输入时用 0 表示），可以用一个 0-100 的自然数来表示，数越大表示越好心。小渊和小轩希望尽可能找好心程度高的同学来帮忙传纸条，即找到来回两条传递路径，使得这两条路径上同学的好心程度只和最大。现在，请你帮助小渊和小轩找到这样的两条路径。
输入
第一行有 2 个用空格隔开的整数 m 和 n，表示班里有 m 行 n 列（1<=m,n<=50）。
接下来的 m 行是一个 m*n 的矩阵，矩阵中第 i 行 j 列的整数表示坐在第 i 行 j 列的学生的好心程度。每行的 n 个整数之间用空格隔开。
输出
共一行，包含一个整数，表示来回两条路上参与传递纸条的学生的好心程度之和的最大值。
样例输入
3 3
0 3 9
2 8 5
5 7 0
样例输出
34
提示
【限制】
30%的数据满足：1<=m,n<=10
100%的数据满足：1<=m,n<=50
题解
最朴素的方法，搜呗。把50拆成25和25，这样效率完全过得去。好了，现在来讲讲另一种方法，一种4维dp。维度其实很好理解了，分别是第一个点的横纵坐标和第二个点的横纵坐标。由于本题是先从左上角走到右下角，再从右下角走到左上角，所以我们可以看作两个点同时从左上角出发，通向右下角。我们还能保证一点，就是我们可以视作两个点速度一样，因为两个点的曼哈顿距离是一样的（曼哈顿距离就是从A位置走到B位置所需的最小步数），又由于两个点不能相遇，所以我们可以视为每时每刻两个点都不会相遇。将问题转化到这里时，我们现在来考虑dp转移。其实有4种转移方式（每个点有2种，从左或从上），就算是不合法的转移，因为我们dp的初值是0，而我们所求的是max，所以也不会影响答案。现在来到最关键的一点：枚举顺序。我们首先要明确一点，就是两个点根本不能相遇，也就更不能交叉，所以必然是一个点在下，一个点在上，搜索的时候依照这一点也能省很多效率.....先不说搜索了，言归正传，于是我们可以定义第一个点的横坐标在相同时刻一定小于第二个点。那我们该从何枚举起呢？自然就是两个点的曼哈顿距离了，然后分别枚举两个点的横坐标就可以确定两个点的坐标。因此这道题就是一道经典的坐标式的dp题目。
参考代码
#include<cstdio>
using namespace std;
int m,n,a[100][100],dp[51][51][51][51];
bool pd(int x,int y)
{
return (x>0)&&(x<=m)&&(y>0)&&(y<=n);
}
int min1(int p,int q) { return p<q?p:q; }
int max1(int p,int q) { return p>q?p:q; }
int main()
{
scanf("%d%d",&m,&n);
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++)
scanf("%d",&a[i][j]);
for(int len=2;len<=m+n;len++)
{
for(int x1=1;x1<len;x1++)
{
int y1=len-x1+1;
if(!pd(x1,y1)) continue;
for(int x2=x1+1;x2<=len;x2++)
{
int y2=len-x2+1;
if(!pd(x2,y2)) continue;
dp[x1][y1][x2][y2]=max1(dp[x1-1][y1][x2-1][y2],
max1(dp[x1-1][y1][x2][y2-1],
max1(dp[x1][y1-1][x2-1][y2],
dp[x1][y1-1][x2][y2-1])));
dp[x1][y1][x2][y2]+=a[x1][y1]+a[x2][y2];
//printf("dp[%d][%d][%d][%d]=%d\n",x1,y1,x2,y2,dp[x1][y1][x2][y2]);
}
}
}
printf("%d",dp[m-1][n][m][n-1]);
return 0;
}
T5：问题 E: 守望者的逃离
题目描述
恶魔猎手尤迪安野心勃勃，他背叛了暗夜精灵，率领深藏在海底的娜迦族企图叛变。守望者在与尤迪安的交锋中遭遇了围杀，被困在一个荒芜的大岛上。为了杀死守望者，尤迪安开始对这个荒岛施咒，这座岛很快就会沉下去。到那时，岛上的所有人都会遇难。守望者的跑步速度为 17m/s，以这样的速度是无法逃离荒岛的。庆幸的是守望者拥有闪烁法术，可在1s 内移动 60m，不过每次使用闪烁法术都会消耗魔法值 10 点。守望者的魔法值恢复的速度为 4 点/s，只有处在原地休息状态时才能恢复。
现在已知守望者的魔法初值 M，他所在的初始位置与岛的出口之间的距离 S，岛沉没的时间 T。你的任务是写一个程序帮助守望者计算如何在最短的时间内逃离荒岛，若不能逃出，则输出守望者在剩下的时间内能走的最远距离。注意：守望者跑步、闪烁或休息活动均以秒(s)为单位，且每次活动的持续时间为整数秒。距离的单位为米(m)。
输入
仅一行，包括空格隔开的三个非负整数 M, S, T。
输出
包含两行：
第1 行为字符串“Yes”或“No”（区分大小写），即守望者是否能逃离荒岛。
第2 行包含一个整数。第一行为“Yes”（区分大小写）时表示守望者逃离荒岛的最短时间；第一行为“No”（区分大小写）时表示守望者能走的最远距离。
样例输入
39 200 4
样例输出
No
197
提示
【输入样例2】
36 255 10
【输出样例2】
Yes
6
【数据规模】
30%的数据满足：1 <= T <= 10, 1 <= S <= 100
50%的数据满足：1 <= T <= 1000, 1 <= S <= 10000
100%的数据满足：1 <= T <= 300000, 0 <= M <= 1000, 1 <= S <= 108。
题解
严格来说，这题不算dp，更像贪心。由于我们知道，闪现肯定在大多数时候是更优的，因此能闪就闪，不能闪就回蓝。但是也会出现闪现等待不如直接往前走的情况，所以我们要同时进行：既有一个s来存走路的，还有一个s来枚举闪现的。一旦走路的没闪现快，就把走路的换成闪现的。每次拿走路的与最终ans比较大小，即可得出正确答案。下面给出的代码以特判为主，所以比较冗杂，但也没有漏掉情况。
参考代码
#include<cstdio>
#define LL long long
using namespace std;
LL t,m,s,dp[300100],ern=0,maxn=-1,st=0;
LL max1(LL p,LL q) { return p>q?p:q; }
int main()
{
scanf("%lld%lld%lld",&m,&s,&t);
ern=m;
for(LL i=1;i<=t;i++)
{
st+=17;
LL pt=(10ll-ern)/4ll;
if(ern%10==2||ern%10==6||ern%10==10) pt++;
if(pt*17ll+dp[i-1]>=s)
{
dp[i]=dp[i-1]+17ll;
if(dp[i]>=s)
{
printf("Yes\n");
printf("%lld",i);
return 0;
}
}
else if((t-i)*4+ern>=10)
{
if(ern>=10)
{
ern-=10ll;
dp[i]=dp[i-1]+60ll;
}
else
{
ern=ern+4ll;
dp[i]=dp[i-1];
}
}
if(dp[i]>st) st=dp[i];
if(st>=s)
{
printf("Yes\n");
printf("%lld",i);
return 0;
}
maxn=max1(maxn,st);
}
printf("No\n");
printf("%lld",maxn);
return 0;
}T6：问题 F: 矩阵取数游戏
题目描述
帅帅经常跟同学玩一个矩阵取数游戏：对于一个给定的n*m的矩阵，矩阵中的每个元素aij均为非负整数。游戏规则如下：
1、每次取数时须从每行各取走一个元素，共 n 个。m 次后取完矩阵所有元素；
2、每次取走的各个元素只能是该元素所在行的行首或行尾；
3、每次取数都有一个得分值，为每行取数的得分之和，每行取数的得分 = 被取走的元素值*2i，其中i表示第i次取数（从 1 开始编号）；
4、游戏结束总得分为 m 次取数得分之和。
帅帅想请你帮忙写一个程序，对于任意矩阵，可以求出取数后的最大得分。
输入
包括 n+1 行：
第1 行为两个用空格隔开的整数 n 和 m。
第2~n+1 行为 n*m 矩阵，其中每行有 m 个用单个空格隔开的非负整数。
输出
仅包含 1 行，为一个整数，即输入矩阵取数后的最大得分。
样例输入
2 3
1 2 3
3 4 2
样例输出
82
提示
【样例 1 解释】
第 1 次：第 1 行取行首元素，第 2 行取行尾元素，本次得分为 1*21+2*21=6；
第 2 次：两行均取行首元素，本次得分为 2*22+3*22=20
第 3 次：得分为 3*23+4*23=56。总得分为 6+20+56=82
【输入样例 2】
1 4
4 5 0 5
【输出样例 2】
122
【输入样例 3】
2 10
96 56 54 46 86 12 23 88 80 43
16 95 18 29 30 53 88 83 64 67
【输出样例 3】
316994
【数据规模】
60%的数据满足：1<=n, m<=30, 答案不超过 1016
100%的数据满足：1<=n, m<=80, 0<=aij<=1000
题解
这道题目前只分享一下思路（状压好打，高精不好打........），首先明白每一行与其他行是互不影响的，因此我们来看某一行。由于该题目是要么从左端取，要么从右端取，因此dp[i][j]表示从左边取了i个，从右边取了j个的最大得分，转移方程也很简单，就是当i不等于0时，看能否由dp[i-1][j]转移而来，同理对于j也是这样。最外层可以枚举一下现在已经取了多少个了，因此最后直接求所有dp[i][j],i+j=当前行总个数，中的最大值，就作为当前行的答案。代码请参考洛谷。
T7：问题 G: 城市交通
题目描述
有n个城市,编号1~n,有些城市之间有路相连，有些则没有,有路则会有一个距离。图所示为一个含有11个城市的交通图,连线上的数(权)表示距离。现在规定只能从编号小的城市到编号大的城市。问:从编号为1的城市到编号为n的城市之间的最短距离是多少?
输入
第1行为n,表示城市数,n≤100。
下面的n行是一个nxn的邻接矩阵map[i,j],其中map[i,j]=0表示城市i和城市j之间没有路相连，否则为两者之间的距离。
输出
一行一个数，表示最短距离。数据保证-定可以从城市1到城市n。
样例输入
11
05300000000
50016300000
30008040000
01000005600
06800005000
03000000080
00400000030
00055000003
00060000004
00000830003
00000003430
样例输出
13
提示
【问题分析]】
逆向思考:现在想要从城市1到达城市11,则只能从城市8、9或10中转过去,如果知道了从城市1到城市8、9和10的最短距离,那么只要把这3个最短距离分别加上这3个城市与城市11之间的距离,再从中取一个最小值即可。这样一来，问题就变成了求城市1到城市8、9、10的最短距离,而这3个子问题与原问题是完全-致的，只是问题的规模缩小了一点。如何求城市1到城市8的最短距离呢?想法与刚才一样,如果知道了城市1到城市4和5的最短距离,那么到城市8的最短距离就是到城市4的最短距离加上5以及到城市5的最短距离加 上5当中较小的那个值。而如何求城市4和5的最短距离呢? ...如此下去,直到求城市1到城市2和3的最短距离，而这个值是已知的(因为城市1和2.3之间有直接的边相连)。这种解题思想就是“动态规划”。
题解
这道题用逆向思维的动规来解决是很容易的，如果你要用图论中的方法（FLOYD、DJ等），那就要注意，只能是标号小的到编号大的，因此还要加一句判断，才能得到正确答案。总的来说，一道基础的图的dp题。哦，还有一道巨坑的地方，输入是n行n列的邻接矩阵，所以输入不能输入字符串（当然是可以直接字符串的）。
参考代码
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std;
struct tree
{
int nxt,to,dis;
}tr[10002];
int head[10002],cnt=0;
void build_tree(int u,int v,int d)
{
tr[++cnt].nxt=head[u];
tr[cnt].dis=d;
tr[cnt].to=v;
head[u]=cnt;
}
int min1(int p,int q)
{
return p<q?p:q;
}
queue<int>q;
int n,dp[10002],ins[10002],vis[10002],d[10002],a[101][101];
int main()
{
memset(d,127/3,sizeof(d));
scanf("%d\n",&n);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
int p;scanf("%d",&p);
if(i!=j)
{
if(p) a[i][j]=p;
else a[i][j]=606706378;
}
}
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(k>=i&&k<=j)
a[i][j]=min1(a[i][j],a[i][k]+a[k][j]);
printf("%d",a[1][n]);
return 0;
}T8:问题 I: 玩具装箱
题目描述
P 教授要去看奥运，但是他舍不得他的玩具，于是他决定把所有的玩具运到北京。
他使用自己的压缩器进行压缩。这个压缩器可以将任意物品变成一维，再放到一种特殊的一维容器中。P 教授有编号为 1…N 的 N 件玩具，第 i 件玩具经过压缩后变成一维，长度为 Ci 。
为了方便整理，P 教授要求在一个一维容器中，玩具的编号是连续的；同时，如果一个一维容器中有多个玩具，那么两件玩具之间要加入一个单位长度的填充物。形式地说，如果要将 i 号玩具到 j 号玩具(i≤j) 放到同一个容器中，则容器长度不小于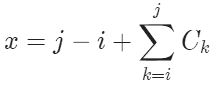
制作容器的费用与容器的长度有关，根据教授研究，如果容器长度为 x，其制作费用为 (X−L)2 ，其中 L 是一个常量。
P 教授不关心容器的数目，他可以制作出任意长度的容器，甚至超过 L。试求最小费用。
输入
第一行输入两个整数 N,L；
接下来 N 行，每行一个整数 Ci 。
输出
输出最小费用。
样例输入
5 4
3
4
2
1
4
样例输出
1
提示
【数据范围与提示】
对于全部数据，1≤N≤5×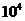
,1≤L,Ci ≤
。
题解
这道题数据强度比较大，因此判定是dp。，我们定义dp[i]表示前i个玩具被装入容器的最小费用，现在我们来看一下，对于任意一个状态，能否转移。假设我们如今枚举到第i个玩具，并且在i之前有dp[j]已经求出，那么我们需要把第j+1到i个玩具装入一个新的容器，即：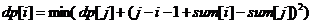 
（0<j<i）
其中:sum[i]表示玩具长度的前缀和。
这样我们可以通过O（n*n）来得到答案。但是这样明显是不够的，我们需要对这个式子进行优化。由于这个式子中出现了平方，因此我们思考能否用斜率优化。
思考有如下状态
，我们思考i应该由j转移而来还是由k转移。为了使问题简化，我们定义：
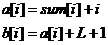
为了判断这一点，我们来做差比大小：
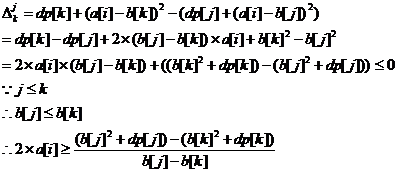
我们发现了什么？这是一个斜率式！点坐标为（b[i],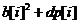
）。
这样有何意义？假设我们将2个点的斜率表示为slope（j,k），那么当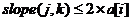
且j<k<i时，显然k更优。因此转化为图像语言为：我们需要维护一个斜率单调递增的队列。一旦我们发现当加入i这点进来后出现了斜率下降的情况，我们就需要先将队列中的元素清除一部分，直到满足条件时，就可以将i压入队。如果我们发现队前面有部分不满足i，那么使队头++。
这样我们每次直接取队首，就是所有满足条件的点中y坐标最小的，也就是答案最小的。见下图：
由于slope(B,C)>slope(A,B)，我们就可以将C入队，否则就需要将B出队....直到满足条件。可以证明，当j<k<i且三者同时在队中时，k一定不是最优的，因此可以通过加入的i清除掉一些无用的元素。
显然，我们最后的答案就是dp[n]。
参考代码
#include<cstdio>
using namespace std;
int n,l,a[50500],sum[50500],q[50500],head=1,tail=1;
long long dp[50500];
int a1(int j) { return sum[j]+j; }
int b(int j) { return a1(j)+1+l; }
int X(int j) { return b(j); }
int Y(int j) { return b(j)*b(j)+dp[j]; }
double slope(int j,int k)
{ return (double)(Y(j)-Y(k))/(double)(X(j)-X(k)); }
int main()
{
scanf("%d%d",&n,&l);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
sum[i]=sum[i-1]+a[i];
}
for(int i=1;i<=n;i++)
{
while(head<tail&&slope(q[head],q[head+1])<2*a1(i)) head++;
dp[i]=dp[q[head]]+(long long)(a1(i)-b(q[head]))*(long long)(a1(i)-b(q[head]));
while(head<tail&&slope(q[tail-1],q[tail])>slope(q[tail],i)) tail--;
q[++tail]=i;
}
printf("%lld",dp[n]);
return 0;
}T9:问题 J: 最长公共上升子序列
题目描述
熊大妈的奶牛在小沐沐的熏陶下开始研究信息题目。
小沐沐先让奶牛研究了最长上升子序列，再让他们研究了最长公共子序列，现在又让他们研究最长公共上升子序列了。
小沐沐说，对于两个数列A和B，如果它们都包含一段位置不一定连续的数，且数值是严格递增的，那么称这一段数是两个数列的公共上升子序列，而所有的公共上升子序列中最长的就是最长公共上升子序列了。
奶牛半懂不懂，小沐沐要你来告诉奶牛什么是最长公共上升子序列。
不过，只要告诉奶牛它的长度就可以了。
数列A和B的长度均不超过3000。
输入
第一行包含一个整数N，表示数列A，B的长度。
第二行包含N个整数，表示数列A。
第三行包含N个整数，表示数列B。
输出
输出一个整数，表示最长公共子序列的长度。
样例输入
4
2 2 1 3
2 1 2 3
样例输出
2
提示
1≤N≤3000，序列中的数字均不超过231−1
题解
这是一道基础的dp进阶。我们可以定义dp[i][j]表示A1到i中，过Bj的最长公共上升子序列的长度。转移的话就很简单，如果a[i]!=b[j]，那么直接dp[i][j]=dp[i-1][j]，而如果相等，就可以由之前k状态转移过来，就是：dp[i][j]=max(dp[i][j],dp[i-1][k]+1)。但是这是一道O（n*n*n）的效率，所以我们需要优化。这道题当然不需要像之前那样斜率优化，只需要单调队列优化就可以很容易用O（n*n）来解决这道题。我们可以很容易发现，在我们进行第2维循环时重复计算了许多步骤，我们能否将求最大值的过程简化？自然是可以的。我们来定义val，每次转移就直接val+1，在得到j的答案后，我们尝试将j联系到val中，即if(b[j]<a[i]) val=max1(val,dp[i-1][j])。这样就能够在规定效率内完成该题。
参考代码
#include<cstdio>
using namespace std;
int n,a[3010],b[3010],dp[3010][3010];
int max1(int a,int b) { return a>b?a:b; }
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<=n;i++) scanf("%d",&b[i]);
for(int i=1;i<=n;i++)
{
int val=0;
for(int j=1;j<=n;j++)
{
if(a[i]==b[j])
dp[i][j]=val+1;
else dp[i][j]=dp[i-1][j];
if(b[j]<a[i]) val=max1(val,dp[i-1][j]);
}
}
int max1=-1;
for(int i=1;i<=n;i++)
if(dp[n][i]>max1) max1=dp[n][i];
printf("%d",max1);
return 0;
}
2399
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
