【图-最短路】 gentree

• 题目描述
• 给你一个无向连通图G，每点有个权值di（>0），要求生成一棵树根为1号节点的有根树T。对于树中边e，e的代价为所有从根出发的且包含e的路径的终点权值的和。现求生成树T，使得边的代价总和最小。
• 输入
• 第一行n,m分别为点数，边数。N <= 100000; m <= 300000;
  接下来m行，每行两个数 u,v描述边的两个端点
  最后一行 n个数，顺次给出每个点的权值
• 输出
• 一个数，最小代价
• 样例输入

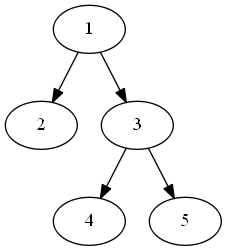
5 4
1 2
1 3
3 4
3 5
1 2 3 4 5

• 样例输出

  23

  先分析题意，就是说这一条边权为经过这一条边的所有边终点权之和。
  可以发现生成的这一棵树中所有边的边权之和恰好等于所有节点深度乘权值。
  
  比如样例数据有：2*1+3*1+4*2+5*2=23
  那么对于同一个节点一定满足这个点的深度最小得到的权值乘深度最小。
  从而得到每一个点的深度最小时得到最优解。
  那么最小的深度就可以跑一遍spfa最短路，得到每个节点和原点的最短路。
  再乘以点权求和即可。
  代码：

#include <iostream> 
#include <cstdio> 
#include <algorithm> 
#include <queue> 
#include <vector> 
#define INF 0xffffff 
using namespace std; 
struct edge{ 
    int from,to,val; 
}; 
vector<edge> e; 
vector<int> node[100000]; 
int value[100000]; 
bool used[100000]={0}; 
int d[100000]={0}; 
void spfa() 
{ 
    fill(d,d+100000,INF); 
    queue<int> q; 
    q.push(1); 
    used[1]=1; 
    d[1]=0; 
    while(!q.empty()) 
    { 
        int u=q.front(); 
        q.pop(); 
        used[u]=0; 
        for(int i=0;i<node[u].size();i++) 
        { 
            if(d[e[node[u][i]].to]>d[u]+e[node[u][i]].val){ 
                d[e[node[u][i]].to]=d[u]+e[node[u][i]].val; 
                if(!used[e[node[u][i]].to]) 
                { 
                    used[e[node[u][i]].to]=1; 
                    q.push(e[node[u][i]].to); 
                } 
            } 
        } 
    } 
} 
int main() 
{ 
    int n,m; 
    scanf("%d%d",&n,&m); 
    for(int i=0;i<m;i++) 
    { 
        int a,b; 
        scanf("%d%d",&a,&b); 
        e.push_back((edge){a,b,1}); 
        node[a].push_back(i); 
    } 
    for(int i=1;i<=n;i++) 
    scanf("%d",&value[i]); 
    spfa(); 
    int ans=0; 
    for(int i=1;i<=n;i++) 
        ans+=d[i]*value[i]; 
    cout<<ans; 
}