Optimization Elemental things+数字IC设计
1.Positive Semidefinite
In linear algebra, a symmetric n × n real matrix M is said to be positive definite if zTMz is positive for every non-zero column vector z of n real numbers. Here zT denotes the transpose of z.
More generally, an n × n Hermitian matrix M is said to be positive definite if z*Mz is real and positive for all non-zero column vectors z of n complex numbers. Here z* denotes the conjugate transpose of z.
The negative definite, positive semi-definite, and negative semi-definite matrices are defined in the same way, except that the expression zTMz or z*Mz is required to be always negative, non-negative, and non-positive, respectively.
Examples:
- The identity matrix
 is positive definite. Seen as a real matrix, it is symmetric, and, for any column vector z with real entries a and b, one has
is positive definite. Seen as a real matrix, it is symmetric, and, for any column vector z with real entries a and b, one has  . Seen as complex matrix, for any column vector z with complex entries a and b one has
. Seen as complex matrix, for any column vector z with complex entries a and b one has  . Either way, the result is positive as long as z is not the zero vector (that is, at least one of a andb is not zero).
. Either way, the result is positive as long as z is not the zero vector (that is, at least one of a andb is not zero).
- The real symmetric matrix
-
-
-
is positive definite since for any non-zero column vector
z with entries
a,
b and
c, we have
-
- This result is a sum of squares, and therefore non-negative; and is zero only if a = b = c = 0, that is, when z is zero.
- The real symmetric matrix
-
-
-
is not positive definite. If
z is the vector
 , one has
, one has
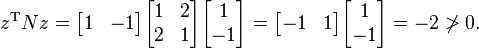
- For any real non-singular matrix
 , the product
, the product 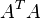 is a positive definite matrix. A simple proof is that for any non-zero vector
is a positive definite matrix. A simple proof is that for any non-zero vector  , the condition
, the condition  since the non-singularity of matrix
since the non-singularity of matrix  means that
means that 
The examples M and N above show that a matrix in which some elements are negative may still be positive-definite, and conversely a matrix whose entries are all positive may not be positive definite.
3rd Chapter-The Design of Architecture
架构的选择和设计又可以分为几个步骤:
1、软硬件划分
2、硬件功能模块划分
3、IP选择和设计
4、模块互连机制的选择和设计
5、架构的建模和仿真验证
应当指出,这些步骤在实际工作中并不是孤立的,而通常都是相互结合和制约的,也没有固定不变的顺序。
1.
进行软硬件划分也是根据系统功能,权衡功能性能要求和实现成本因素的结果。
硬件功能单元实现最快的运算速度,达到最佳的性能,但其缺点是缺少灵活性,实现难度大,开发周期长,风险大。
DSP相对于特定的应用和运算可以提供好的性能,相对开发的难度低,时间较短,风险较低,同时也具备一定的灵活性。
CPU提供了最灵活的功能,同时运算性能也是最差的。
所以,得出如下结论:
对于那些对性能(延时)有着严格要求的功能(如算法复杂度很高信道编解码等),选择硬件功能模块来实现;
对于性能有一定要求,同时要求有一些灵活性的功能(如语音编码等),我们选择在DSP上用固件实现;
对于那些系统控制功能(如协议栈,用户接口等),我们在CPU上的软件方式实现。
2. 就是要建立一个芯片的功能框图。模块的接口设计对于设计的重用性至关重要。
3. 是否有相类似的设计?是否可以重用?是否自己小组成员设计过?是否存在第三方IP?还需要定制?第三方IP是否可加速?成本是否过高?
4.IP核通常分为硬核(前后),软核(前)和固核(布局布线)。
存储器单元通常有晶体管级由手工设计完成,然后使用编译器(Memory Compiler)来生成存储器阵列。模拟模块,包括A/D、D/A转换单元,以及锁相环电路(PLL)等至少部分设计是在晶体管级完成的,因此上述电路只能使用硬核。
几乎所有的其他数字设计,都始于软核,经过综合、布局布线等步骤将RTL代码映射到门级电路,然后再映射GDSII。从RTL到GDSII的过程称之为硬化(Hardening),集成硬化后的数字IP模块与其他集成硬核的过程是一样的。
5. 片上总线和片上网络。
芯片设计的特殊考虑:
1.设计的层次化
2.时序闭合性设计(接口设计-在重要模块前后加入register,)








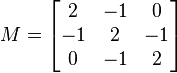

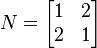














 689
689

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








