网络流（1）

最新推荐文章于 2021-11-02 19:59:43 发布

pkueecscss

最新推荐文章于 2021-11-02 19:59:43 发布

阅读量337

点赞数

文章标签：算法网络流

本文链接：https://blog.csdn.net/pkueecscss/article/details/89352843

版权

算法专栏收录该内容

7 篇文章 0 订阅

订阅专栏

网络流(1)

基本概念和性质

原文见我的博客

最小割

设容量网络 $\subset V 且 s ∈ A,t ∈ V-A ,称(A,V-A) = \{ <i,j> | <i,j> ∈ E 且 i ∈ A , j ∈ V-A \}$ 为N的割集, $\sum_{ <i,h> ∈ (A,\bar{A}) } c(i,j)$ 为割集 $c (A, V - A) $ 的容量，容量最小的割集称为最小割集。

引理1

设容量网络 $N = < V, E, c, s, t >$ ,f为N上的任一可行流， $\subset V 且 s ∈ A , t ∈ V-A,则 v(f) = \sum_{<i,j> ∈ (A,\bar{A})} f(i,j) - \sum_{ <j,i>∈ (A,\bar{A})} f(j,i)$

引理2

设f是任一可行流，(A,V-A)是任一割集，则 $\leq c(A,V-A)$

引理3

设f是一个可行流，(A,V-A)是一个割集。如果 $v (f) = c (A, V - A)$ ,则f是最大流，(A,V-A)为最小割集

增广链

设容量网络 $N = < V, E, c, s, f >$ ,f为N上的一个可行流

N中流量等于容量的边称为饱和边，否则称为非饱和边
流量等于0的边称为零流边，否则为非零流边
不考虑边的方向，N中从顶点i到顶点j的一条边不重复的路径称做i-j链，链的方向为从i到j。链中与链的方向一致的边称作前向边，否则称为后向边。
如果链中所有前向边都是非饱和的，所有后向边都是非零流的，则称这条链为i-j增广链

最大流的性质

定理1

可行流f为最大流等价于不存在关于f的s-t增广链

证明： 1555296858689

1555296884115

定理2(最大流最小割集定理)

容量网络的最大流的流量等于最小割集的容量。

Fold-Fulkeson算法

思想

从给定初始可行流(通常取零流开始)，取当前可行流的s-t增广链P,修改P上流量得到新的可行流，重复进行，直到不存在s-t增广链为止

形象的理解

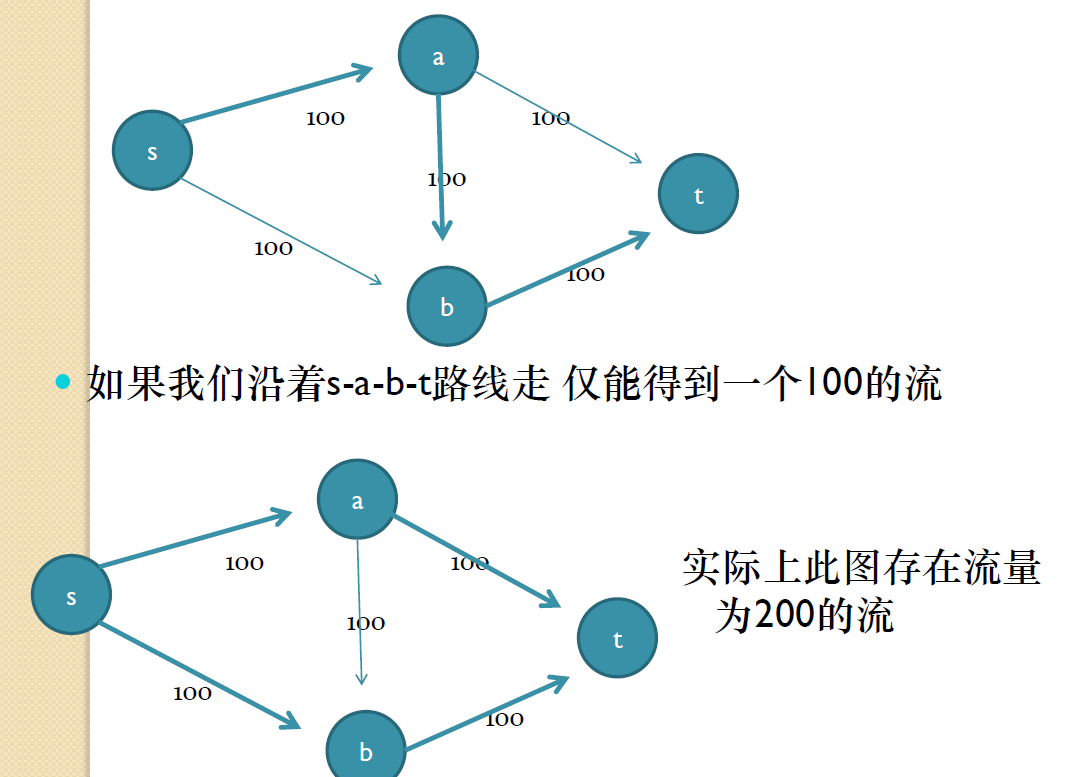
伪代码

顶点j得到标号表示已经找到从s到j的增广链，标号为 $(l_j,\delta_j)$ ,其中 $\delta_j$ 等于直到j为止链上所有前向边的容量和流量之差以及所有后向边的流量的最小值，$l_j = +i $或$ l_j = -i $, 前者表示链是从 i 到 j 且$ <i,j> $是前向边，后者表示链是从 i 到 j 且$ <i,j>$是后向边。

时间复杂度

假设所有容量都是正整数，则算法时间复杂度为 $O (m C)$ ,m为边数， $\sum_{<s,j>∈ E}c(s,j)$ 。(每次流量至少加1，至多C个阶段)，而每阶段标号和修改增广链流量都需要O(m)

改进方法

每次求最短的s-t增广链，即用bfs代替dfs找增广链，Edmonds-Karp算法， $O(nm^2)$

以POJ1273题为例，链接http://poj.org/problem?id=1273

#include<iostream>
#include<queue>
#include<cstring>
#include<cmath>

using namespace std;
int N,M ;
int G[300][300] = {} ;
int Prev[300] = {} ;
bool vis[300] = {} ;
unsigned Augument()
{
	int v ;
	queue<int> q ;
	memset(Prev,0,sizeof(Prev)) ;
	memset(vis,0,sizeof(vis)) ;
	Prev[1] = 0 ;
	vis[1] = 1 ;
	q.push(1) ;
	bool found = 0 ;
	while ( !q.empty() ) {
		v = q.front() ;
		q.pop() ;
		for (int i = 1 ; i <= M ; ++i ) {
			if ( G[v][i] > 0 && vis[i] == 0 ) {
				Prev[i] = v ;
				vis[i] = 1 ;
				if ( i == M ) {
					found = 1 ;
					while( !q.empty() ) q.pop() ;
					break ;
				}
				else {
					q.push(i) ;
				}
			}
		}
	}
	if ( !found ) return 0 ;
	int nMinFlow = 1 << 30 ;
	v = M ;
	while( Prev[v] ) {
		nMinFlow = min(nMinFlow,G[Prev[v]][v]) ;
		v = Prev[v] ;
	}
	v = M ;
	while( Prev[v] ) {
		G[Prev[v]][v] -= nMinFlow ;
		G[v][Prev[v]] += nMinFlow ;
		v = Prev[v] ;
	
	}
	
	return nMinFlow ;
}
int main () {
	while( cin >> N >> M ) {
		int s,e,c ;
		memset(G,0,sizeof(G)) ;
		for ( int i = 0 ; i < N ; ++i ) {
			cin >> s >> e >> c ;
			G[s][e] += c ;
		}
		unsigned ans = 0 ,aug = 0 ;
		while( aug = Augument() ) {
			ans += aug ;
		}
		cout << ans << endl ;
	}
	return 0;
}

一次标号修改尽可能多条s-t增广链上的流量——Dinic算法

Dinic算法

辅助网络（残余网络）

证明正确性的基础——引理4和引理5(详细证明过于繁琐，略去)

引理4

引理5

算法实现

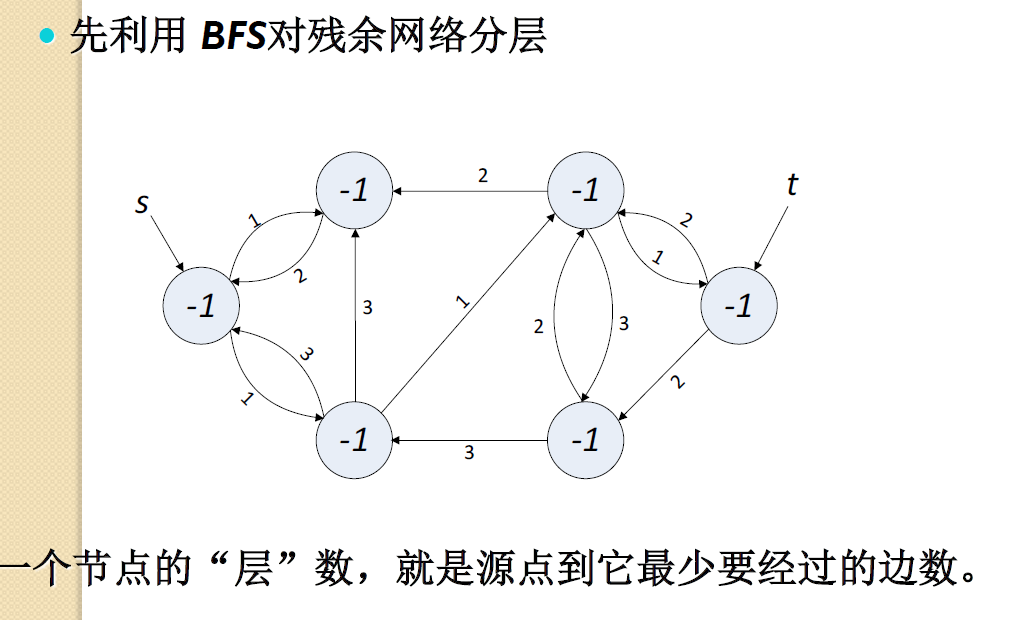
C++代码

C++代码（残余网络版，模板题链接http://bailian.openjudge.cn/practice/1469/）

#include <iostream>
#include <queue>
#include<bits/stdc++.h>
using namespace std;
int G[1000][1000];
int Prev[1000]; //路径上每个节点的前驱节点
bool Visited[1000];
int Layer[1000];   //Layer[i]是节点i的层号  
int n,m,p;  //m是顶点数目，顶点编号从1开始 1是源，m是汇, n是边数

bool CountLayer()   { //分层
	int layer = 0;     
	deque<int>q;
	memset(Layer,0xff,sizeof(Layer)); //都初始化成-1
	Layer[1] = 0;  q.push_back(1);
	while( ! q.empty()) {
		int v = q.front();
		q.pop_front();
		for( int j = 1; j <= m; j ++ ) {
			if( G[v][j] > 0 && Layer[j] == -1 ) {
			//Layer[j] == -1 说明j还没有访问过
				Layer[j] = Layer[v] + 1; 
				if( j == m ) return true;  //分层到汇点即可
				else q.push_back(j);
			}
		}
	}
	return false;
}
int Dinic() {
	int i;  	
	int s;
	int nMaxFlow = 0;
	deque<int> q; //DFS用的栈
	while( CountLayer() ) { //只要能分层
		q.push_back(1);	//源点入栈	
		memset(Visited,0,sizeof(Visited));   
		Visited[1] = 1;
		while( !q.empty()) {
			int nd = q.back();
			if( nd == m ) { // nd是汇点
				//在栈中找容量最小边
				int nMinC = 1 << 20;
				int nMinC_vs; //容量最小边的起点
				for( i = 1;i < q.size(); i ++ ) {
					int vs = q[i-1];
					int ve = q[i];
					if( G[vs][ve] > 0 ) {
						if( nMinC > G[vs][ve] ) {
							nMinC = G[vs][ve];
							nMinC_vs = vs;
						}
					}
				}
				//增广，改图
				nMaxFlow += nMinC;
				for( i = 1;i < q.size(); i ++ ) {
					int vs = q[i-1];
					int ve = q[i];
					G[vs][ve] -= nMinC; //修改边容量 
					G[ve][vs] += nMinC; //添加反向边
				}
				//退栈到 nMinC_vs成为栈顶，以便继续dfs
				while( !q.empty() && q.back() != nMinC_vs ) { 
					Visited[q.back()] = 0; 
					q.pop_back();
				}

			}
			else { //nd不是汇点
				for( i = 1;i <= m; i ++ )  {
				      if( G[nd][i] > 0 && Layer[i] == Layer[nd] + 1 &&
				   	! Visited[i]) {
						//只往下一层的没有走过的节点走
						Visited[i] = 1;
						q.push_back(i);
						break;
					}
				}
				if( i > m)  //找不到下一个点
					q.pop_back(); //回溯
			}
		}
	}
	return nMaxFlow;
}

int main()
{
	int T ;
	scanf("%d",&T) ;
	while (T-- ) {
		//m是顶点数目，顶点编号从1开始
		scanf("%d %d",&p,&n) ;
		int i,j,k;
		int s,e,c;
		memset( G,0,sizeof(G)) ;
		for( i = 1;i <= p;i ++ ) {
			scanf("%d",&c) ;
			for ( j = 1 ; j <= c ; ++j ) {
				scanf("%d",&e) ;
				G[e+1][i+n+1] = 1 ;
		
			}
		}
		for(int i = 1 ; i <= n ; ++i ) {
			G[1][i+1] = 1 ; 
	
		} 
		for(int i = 1 ; i <= p ; ++i ) {
			G[i+n+1][p+n+2] = 1 ;
	
		}
		m = p+n+2 ;
		unsigned int MaxFlow = Dinic();
		if(MaxFlow == p ) printf("YES\n") ;
		else printf("NO\n") ;
	}
	return 0;
}

pkueecscss

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
网络流（1）

网络流(1)基本概念和性质最小割设容量网络N=&lt;V,E,c,s,t&gt;,A⊂V且s∈A,t∈V−A,称(A,V−A)={&lt;i,j&gt;∣&lt;i,j&gt;∈E且i∈A,j∈V−A}N = &lt;V,E,c,s,t&gt;,A \subset V 且 s ∈ A,t ∈ V-A ,称(A,V-A) = \{...
复制链接

扫一扫