转载地址:http://blog.csdn.net/frankyzhangc/article/details/6990782 自己也做了一定的添加和修改
想要深刻理解矩阵的卷积,那么首先要知道什么是离散序列的卷积。
已知离散序列x(n)和h(n),则x(n)和h(n)的卷积定义为:
其计算过程是对h(n)翻转,平移,相乘,求和。也可以用不进位乘法计算,并且Length(y)=Length(x)+Length(h)。
还有,若x(n):n1≤n≤n2;h(n):n3≤n≤n4;那么y(n):n1+n3≤n≤n2+n4
一个矩阵与另一个矩阵的卷积运算大部分运用在图像处理上,例如用一个模板去对一幅图像进行卷积。我们这里只考虑n*n的模板,并且n为奇数(当然不是方阵或者n不是奇数也可以,但是在实际应用中模板大都为n为奇数的方阵)。
把模板(n*n)放在矩阵上(中心对准要处理的元素),用模板的每个元素去乘矩阵中的的元素,累加和等于这个元素,依次计算每个元素的值,如果矩阵的中心在边缘就要将原矩阵进行扩展,例如补0,或者直接规定模板的中心距离边缘(n-1)/2个单位以上。
卷积的计算步骤:
(1) 卷积核绕自己的核心元素顺时针旋转180度(这个千万不要忘了)
(2) 移动卷积核的中心元素,使它位于输入图像待处理像素的正上方
(3) 在旋转后的卷积核中,将输入图像的像素值作为权重相乘
(4) 第三步各结果的和做为该输入像素对应的输出像素
以下举一个简单的例子,并用Matlab来观察
相关MATALB代码
a=[2 1 3 1;1 2 1 2;2 1 3 2;1 3 1 2];%大小为ma*na
b=[1 1 1;1 1 1;1 1 1];%大小为mb*nb
c=conv2(a,b,'same');%返回和a同样大小的部分,ma*na,一般在图像中的应用都是这样使用
d=conv2(a,b,'full');%返回完整矩阵,大小为(ma+mb-1,na+nb-1)
fprintf('\na = \n');
disp(a);
fprintf('\nb = \n');
disp(b);
fprintf('\nc = \n');
disp(c);
fprintf('\nd = \n');
disp(d);
MATALB仿真结果
a =
2 1 3 1
1 2 1 2
2 1 3 2
1 3 1 2
b =
1 1 1
1 1 1
1 1 1
c =
6 10 10 7
9 16 16 12
10 15 17 11
7 11 12 8
d =
2 3 6 5 4 1
3 6 10 10 7 3
5 9 16 16 12 5
4 10 15 17 11 6
3 7 11 12 8 4
1 4 5 6 3 2








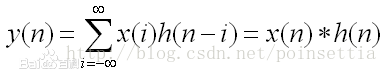














 7382
7382

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








