负指数信号梯形成型方法浅析

前言

负指数信号是含电容电路中极易产生的一种信号类型。对于常见的核脉冲信号，由于探测器所产生的探测到的信号一般为带电粒子定向移动所产生的电流信号，为将该电流信号向电压信号进行转换，需要在前放中加入电容(理想型电流灵敏型前放除外，但实际上即使是电流灵敏型前放也必定存在一些寄生电容)。由于电容的放电规律在时域中为负指数变化，所以需要处理的核脉冲信号往往是负指数型的(在实际处理过程中往往是双负指数信号)。
有鉴于此，对负指数信号和双负指数信号进行处理，有利于更进一步提取负指数或双负指数信号中的幅度信息和时间信息。

常见的负指数信号处理方法简介

最佳滤波器

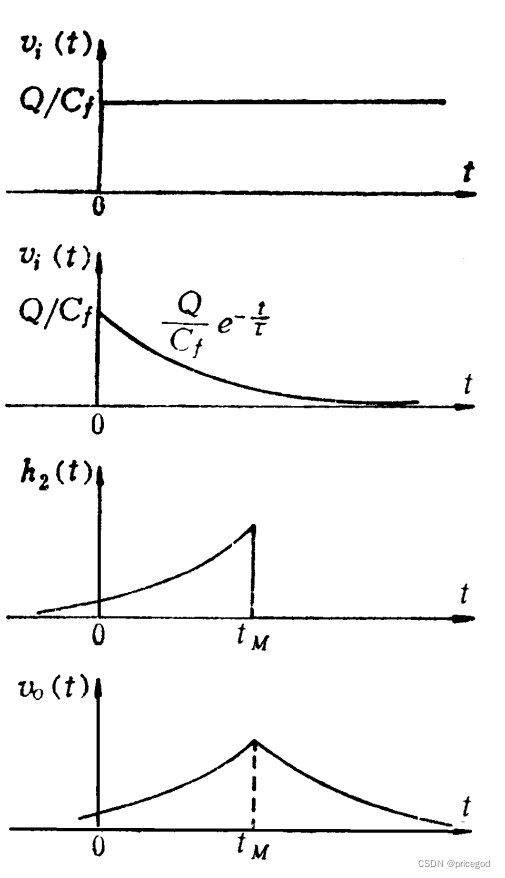
首先需要明白的是，早在1968年，便由Radeka.V得到了具有最佳信噪比的核脉冲信号成型的数学表达式和信号形状，这类滤波器主要由针对白噪声的白化滤波器和针对非白噪声的匹配滤波器两部分组成。遗憾的是由于匹配滤波器中具有镜像关系，在以单位阶跃信号为输入的情况下，最佳滤波器的输出信号为两边无限宽的指数衰减尖顶脉冲。这便要求了在信号输入前便已经有了该信号的响应，所以这一系统是非因果的，因此在实际的物理世界中难以进行实现。以下给出单位阶跃信号下的最佳滤波器成型结果图(Note:图片并非原创)：

所以现在的各类为提高信噪比的滤波器都只是将滤波结果向最佳滤波器进行靠拢，以期得到较好的滤波结果。

目前的核脉冲数字成型方法主要分为两类，其中一类为梯形成型算法，而另外一类为高斯成型算法。

梯形成型滤波器

对于梯形成型算法主要有两类实现方式，其一是将负指数信号和成型后的梯形信号进行Z变换，并将两者的变换结果在Z域中相除来得到系统函数，再将系统函数进行逆Z变换得到时域中的滤波器表达式，从而完成梯形成型数字滤波器的构建，这种方法的详细介绍可参考：梯形成形算法中成形参数与成形脉冲波形关系研究。其二是直接在时域中通过简单信号的卷积结果直接在时域中构建出梯形信号，但这一方法在现在国内的文献中还有部分表述不清，在后面会对这一方法进行详细论述。

高斯成型滤波器

对高斯成型算法据笔者目前所知主要包含三类，其一为通过小波分析实现高斯成型。其二为对SK滤波器进行数字化完成高斯成型。其三为对CR-nRC电路进行数字化完成高斯成型。(NOTE：以上导向的论文只是笔者认为具有一定代表性的论文，并非业界共识)

关于梯形成型函数卷积法的讨论（正文）

函数卷积法的背景

在笔者开始关心梯形成型算法时，发现目前网络与学术界可能将更多的注意力投入于通过Z域进行梯形成型这一方法上。但在这一方法的迭代过程中便存在着除法运算，这使得该方法通过逻辑电路(特别是FPGA)进行实现具有一定的难度，目前较多人通过Matlab中的simulink进行数学过程的搭建，然后直接生成相应的Verilog代码，但这的确涉及到版权问题。因此在这里介绍通过函数卷积法实现梯形成型的推导和结论，这一方法仅仅在归一化时需要进行除法运算，可使用可编程逻辑电路比较方便地搭建出相应的滤波器。（NOTE：这一推导过程由 Jordanov于1994年提出，但在其论文中未详细介绍将连续时域中的结果写成离散时域递推形式的方法，在此本文添加上这部分的数学过程，使推导更为连贯）

函数卷积法的推导过程

假设理想核脉冲负指数表达式如下：
$$v_i(t)=A{e}^{-\frac{t}{\tau }}u(t)\text{\hspace{1em}(1)}$$其中$v_i(t)$代表输入系统的负指数脉冲信号在时域中的表达形式，$A$为信号幅度，$t$为实际测量时刻点，$\tau$为脉冲衰减时间常数，$u(t)$为单位阶跃信号。
另外假设门函数的表达式如下：
$$h_2(t)=\{\begin{array}{rl}0& t<0,\\ 1& 0\le t<T_2,\\ 0& t\ge T_2.\end{array}\text{\hspace{1em}(2)}$$
其中$T_2$为门函数下降沿所在时刻点。
同理假设锯齿函数(类似于数学中的正比函数与门函数的乘积)的表达式如下
$$h_1(t)=\{\begin{array}{rl}0& t<0,\\ t& 0\le t<T_1,\\ 0& t\ge T_1.\end{array}\text{\hspace{1em}(3)}$$
同$h_2(t)$中的$T_2$，$T_1$为锯齿函数的下降沿所在时刻点。
为方便对表达式$(1)\sim (3)$的有更感性的认识，在此给出三个函数的图像如下,在图像中$A=1,\tau =20,T_2=20,T_1=20$：

在已知三种函数表达式的情况下可通过图像法得到$v_i(t)$分别同$h_2(t)$和$h_1(t)$的卷积结果。(Note:对这两个卷积的计算方法可参考《信号与系统》的相关专著，大部分信号与系统教材均会对其过程进行详细介绍，在此本文不再赘述)
假设$v_i(t)$同$h_2(t)$的卷积结果可写作函数$p(t)$，则可得下式(Note:为进行计算简化，在此认为$v_i(t)$的幅度$A=1$)：
$$p(t)=v_i(t)\ast h_2(t)={\int }_{-\infty }^{\infty }{v}_i(t^{\prime })h_2(t-t^{\prime })d{t}^{\prime }=\{\begin{array}{ll}0& t<0,\\ \tau (1-e^{-\frac{t}{\tau }})& 0\le t<T_2,\\ \tau e^{-\frac{t}{\tau }}(e^{-\frac{T_2}{\tau }}-1)& t\ge T_2\end{array}\text{\hspace{1em}(4)}$$
其中$t^{\prime }$为卷积计算中的临时变量，其他变量均已出现并介绍过，在此不再进行赘述。
同理，将$v_i(t)$同$h_1(t)$的卷积结果写作函数$r(t)$，则可得$r(t)$的表达式为(Note:在此同样令$A=1$)：
$$\begin{array}{rl}r(t)& =v_i(t)\ast h_1(t)={\int }_{-\infty }^{\infty }{v}_i(t^{\prime })h_1(t-t^{\prime })d{t}^{\prime }\\ & =\{\begin{array}{ll}0& t<0,\\ t\tau +{\tau }^2{e}^{-\frac{t}{\tau }}-{\tau }^2& 0\le t<T_1,\\ {\tau }^2{e}^{-\frac{t}{\tau }}+\tau T_1{e}^{\frac{T_1-t}{\tau }}-{\tau }^2{e}^{\frac{T_1-t}{\tau }}& t\ge T_1\end{array}\end{array}\text{\hspace{1em}(5)}$$
通过对$p(t)$与$r(t)$进行观察可以发现，当$0\le t<T_1$且同时满足$0\le t<T_2$时，有：
$$\tau p(t)+r(t)={\tau }^2(1-e^{-\frac{t}{\tau }})+t\tau -{\tau }^2(1-e^{-\frac{t}{\tau }})=t\tau \text{\hspace{1em}(6)}$$
可发现式$(6)$这一数学形式表示从原点出发以斜率$\tau$上升的一条直线，其恰好满足梯形的左上升沿的应该具有的数学形式。
为进行梯形平顶的构建，需要找到为常数的梯形平顶高。为此首先假设$T_1<T_2$时，且$T_1\le t<T_2$时，已经构建完成的$\tau p(t)+r(t)$可以写作：
$$\begin{array}{rl}\tau p(t)+r(t)& ={\tau }^2-{\tau }^2{e}^{-\frac{t}{\tau }}+{\tau }^2{e}^{-\frac{t}{\tau }}+\tau T_1{e}^{\frac{T_1-t}{\tau }}-{\tau }^2{e}^{\frac{T_1-t}{\tau }}\\ & ={\tau }^2+\tau T_1{e}^{\frac{T_1-t}{\tau }}-{\tau }^2{e}^{\frac{T_1-t}{\tau }}\end{array}\text{\hspace{1em}(7)}$$
为将$(7)$中的$e^{\frac{T_1-t}{\tau }}$项消去，发现可将$p(t)$进行坐标变换以构建含有$e^{\frac{T_1-t}{\tau }}$项的表达式。并且引入$p(t-T_1)$项便可以引入$e^{\frac{T_1-t}{\tau }}$，而为了不引入含有$T_2$的项，则需要保证$0\le t-T_1<T_2$，也亦$T_1\le t<T_1+T_2$。由于不清楚$p(t-T_1)$的系数，在此设其系数为$a$以保证能够将$e^{\frac{T_1-t}{\tau }}$项完全消去。则可得下式：
$$\begin{array}{rl}\tau p(t)+r(t)+ap(t-T_1)& ={\tau }^2+\tau T_1{e}^{\frac{T_1-t}{\tau }}-{\tau }^2{e}^{\frac{T_1-t}{\tau }}+a\tau -a\tau e^{\frac{T_1-t}{\tau }}\\ & ={\tau }^2+a\tau +\tau e^{\frac{T_1-t}{\tau }}(T_1-\tau -a)\end{array}\text{\hspace{1em}(8)}$$
根据式$(8)$可知，当$a=T_1-\tau$时，式$(8)$会成为一个常数，这一常数值为：
$$\tau p(t)+r(t)+ap(t-T_1)={\tau }^2+a\tau ={\tau }^2+(T_1-\tau )\tau =T_1\tau \text{\hspace{1em}(9)}$$
通过式$(6)$与式$(9)$可得，梯形上升沿持续时间为$T_1$而梯形上平顶高度为$T_1\tau$。
而为使最终的所成的梯形为对称状态，在已知上升沿和平顶表达式的情况下可直接给出下降沿以及后续的函数表达式，假设后续梯形的完整函数用符号$s(t)$l来进行表示，则有：
$$s(t)=\{\begin{array}{ll}0& t<0,\\ t\tau & 0\le t<T_1,\\ T_1\tau & T_1\le t<T_2,\\ T_1\tau -\tau (t-T_2)& T_2\le t<T_1+T_2,\\ 0& t\ge T_1+T_2\end{array}\text{\hspace{1em}(10)}$$
成型完成后的梯形应该如下图所示：

为实现以上梯形，设有一函数$Q(t)$，使得$s(t)=\tau p(t)+r(t)+ap(t-T_1)+Q(t)$，则可得$Q(t)=s(t)-[\tau p(t)+r(t)+ap(t-T_1)]$,考虑到式中$s(t)、p(t)、r(t)、a、p(t-T_1)$的形式均为已知，则可求得$Q(t)$的表达式如下：
$$Q(t)=\{\begin{array}{ll}0& t<T_2,\\ {\tau }^2-t\tau +T_2\tau -{\tau }^2{e}^{\frac{T_2-t}{\tau }}& T_2\le t<T_1+T_2,\\ {\tau }^2{e}^{\frac{T_1+T_2-t}{\tau }}-T_1\tau e^{\frac{T_1+T_2-t}{\tau }}-{\tau }^2{e}^{\frac{T_2-t}{\tau }}& t\ge T_1+T_2\end{array}\text{\hspace{1em}(11)}$$
通过对$Q(t)$的表达式进行观察可以发现，实际上$Q(t)=-r(t-T_2)$,则可对$s(t)$的形式可重新进行改写：
$$s(t)=\tau p(t)+r(t)+(T_1-\tau )p(t-T_1)-r(t-T_2)\text{\hspace{1em}(12)}$$
在将$p(t)$和$r(t)$改写为$v_i(t)$与$h_2(t)$和$h_1(t)$卷积的形式，便可得：
$$s(t)=v_i(t)\ast (h_1(t)+\tau h_2(t)+(T_1-\tau )h_2(t-T_1)-h_1(t-T_2))\text{\hspace{1em}(13)}$$
则可得系统的单位冲击响应函数$h(t)$为：
$$\begin{array}{r}h(t)=(h_1(t)+\tau h_2(t)+(T_1-\tau )h_2(t-T_1)-h_1(t-T_2)\end{array}\text{\hspace{1em}(14)}$$
经过上述推导，便得到了连续时域中的单位冲击响应函数，为方便使用FPGA等数字器件实现算法，还需要将以上连续时域中的单位冲击响应函数转化为离散时域中的递推形式，对于这种递推形式的转化目前笔者所能接触到的资料较少，Jordanov的文章中只给出了通过变换积分上下限的方式得到门函数$h_2(t)$的离散递推形式的方法，但是这一方法难以得到锯齿函数的离散递推表达式。在此通过单位冲击函数和单位阶跃函数的卷积性质得到门函数和锯齿函数在离散时域中的递推表达式。
首先进行较为简单的门函数的递推形式的导出。对门函数而言，其可表示为两单位阶跃函数之差的形式。假设将连续时域转化为离散时域时，离散时域的采样时间(即两个相邻的离散数据点之间的对应的采样时刻点之差)为$T_{采样}$，则式$(2)$中的$T_2$可以表示为$T_2=T_{采样}\times l$，其中$l$便是$T_2$的离散值，也为门函数在离散时域中的宽度。则门函数$h_2(t)$在离散时域中可写作：
$$h_2(t)=u[n]-u[n-l]\text{\hspace{1em}(15)}$$
在式$(15)$中，$u[n]$为单位阶跃函数，$u[n-l]$为单位阶跃函数向坐标轴右端平移$l$个单位后的结果。两者相减便能够得到门函数。
对单位阶跃信号而言，其具有卷积特性。假设存在一输入信号可表示为$a[n]$，其与单位阶跃信号进行卷积的结果如下图所示：
$$a[n]\ast u[n]=\sum _{k=-\infty }^{n}a[k]\text{\hspace{1em}(16)}$$
而对于单位冲击信号$\delta [n]$，其同样具有卷积特性，可表示如下：
$$a[n]\ast \delta [n-b]=a[n-b]\text{\hspace{1em}(17)}$$
则$h_2[n]$同$v_i[n]$进行卷积得到的$p[n]$的表达式为：
$$\begin{array}{rl}p[n]& =v_i[n]\ast h_2[n]=v_i[n]\ast (u[n]-u[n-l])\\ & =v_i[n]\ast u[n]-v_i[n]\ast u[n-l]\\ & =v_i[n]\ast u[n]-v_i[n]\ast \delta [n-l]\ast u[n]\\ & =v_i[n]\ast u[n]-v_i[n-l]\ast u[n]\\ & =\sum _{i=-\infty }^n(v_i[i]-v_i[n-l])\end{array}\text{\hspace{1em}(18)}$$
通过式$(18)$易得$p[n]$的递推形式：
$$p[n]=p[n-1]+v_i[n]-v_i[n-l]\text{\hspace{1em}(19)}$$
对锯齿函数而言，可认为其是对某一门函数进行积分，再减去与门函数长度同高的阶跃函数得到，其中对从0时刻开始，长度为$k$的门函数进行积分所得到的结果可见下图：

在假设长度为$k$的门函数在离散时域中的函数符号为$h_3[n]$，则锯齿函数$h_1[n]$可表示为：
$$h_1[n]=h_3[n]\ast u[n]-ku[n-k]\text{\hspace{1em}(20)}$$
在式$(20)$中将门函数$h_3[n]$的积分写作其与单位阶跃函数$u[n]$的卷积。并且由于门函数$h_3[n]$的长度$k$实际上就是锯齿函数的非零部分的长度，由此可得$T_1=T_{采样}\times k$，则可知$k$实际上便是式$(3)$中$T_1$的离散化结果。在以上论述下，可得锯齿函数$h_1[n]$同输入函数$v_i[n]$卷积的结果$r[n]$的形式为：
$$\begin{array}{rl}r[n]& =h_1[n]\ast v_i[n]=h_3[n]\ast u[n]\ast v_i[n]-ku[n-k]\ast v_i[n]\\ & =(u[n]-u[n-k])\ast v_i[n]\ast u[n]-k\delta [n-k]\ast v_i[n]\ast u[n]\\ & =\left[\right(\sum _{j=-\infty }^n(v_i[j]-v_i[j-k]))-k{v}_i[n-k]]\ast u[n]\\ & =\sum _{i=-\infty }^n\left\{\sum _{j=-\infty }^i\right[v_i[j]-v_i[j-k]]-k{v}_i[i-k]\}\end{array}\text{\hspace{1em}(21)}$$
对$r[n]$可以写成以下递推形式：
$$\begin{array}{rl}r[n]& =r[n-1]+\sum _{j=-\infty }^n[v_i[j]-v_i[j-k]]-k{v}_i[n-k]\\ & =r[n-1]+p[n]-k{v}_i[n-k]\end{array}\text{\hspace{1em}(22)}$$
将式$(21)$和式$(22)$带入式$(12)$中便能够得到梯形成型的离散时域递推表达式：
$$s[n]=r[n]+Mp[n]+(k-M)p[n-k]-r[n-l]\text{\hspace{1em}(23)}$$
在式$(23)$中$M$为式$(1)$中的负指数信号衰减时间常数$\tau$的离散化值，两者满足$\tau =T_{采样}\times M$。将$r[n]$与$p[n]$的递推形式带入后可得$s[n]$的递推形式：
$$s[n]=s[n-1]+p^{\prime }[n-1]+(M+1)d^{k,l}[n]\text{\hspace{1em}(24)}$$
其中$p^{\prime }[n]$和$d^{k,l}[n]$为中间变量，其可写作：
$$p^{\prime }[n]=p^{\prime }[n-1]+d^{k,l}[n]\text{\hspace{1em}(25)}$$
$$d^{k,l}[n]=v_i[n]-v_i[n-k]-v_i[n-l]+v_i[n-k-l]\text{\hspace{1em}(26)}$$
综上，式$(24),(25)$和$(26)$便是梯形成型的主要算法，其能单纯地根据输入信号进行加减和乘法运算将负指数信号转化为梯形信号，这也使得该算法极易通过FPGA进行实现。
另外，通过式$(10)$可以看到对幅度为1的负指数信号脉冲经过梯形成型后便会被放大至$T_1\tau$,替换成经过离散化的变量表示便是会被放大为原来的$kM$倍，据此，如果需要还原输入信号的脉冲幅度，则需要将最终幅度除以$kM$。

函数卷积法的Python实现

根据前面所讨论的，梯形成型算法主要存在三个需要提前设置的参数，这三个参数分别为$k、M$和$l$,其中$k$和$l$分别决定了梯形上升沿和上升沿与平顶的总长度，由$l-k$决定了梯形平顶的长度。而参数$M$则直接决定了成型的形状(Note:$M$过小会将成型梯形的下降沿上扬，而$M$过大则会将成型梯形的上升沿下扬)。

参数$M$由负指数信号的衰减时间常数离散化而来，所以可以根据负指数信号脉冲的衰减时间常数除以采样时间所得到，也便是$M=\frac{\tau }{T_{采样}}$。但是实际负指数信号的衰减时间常数很难获得，因此需要不断对$M$值进行调整，以获得最完美的梯形成型。
在此给出笔者通过Python完成的梯形成型的函数：

#进行梯形成型函数模块的编写


#完成数据处理部分的程序编写
def calculateshape(y,k,l,M):                                                      #定义成型算法函数

    #完成对dk,l(n)函数的计算 
    s=[]                                                                    #定义空的s列表，用于储存输入
    p=[]                                                                    #定义空的p列表，用于进行p函数的迭代
    d=[]                                                                    #定义空的d列表，用于对d(k,l)进行储存
    for i in range(0,len(y)):                                               #对整个y循环进行遍历
        d.append(y[i])                                                      #对d赋予初值
        if i >= k:                                                          #当i的值大于k时
            d[i]=d[i]-y[i-k]                                                #用于进行d的第一步迭代
        else:
            d[i]=d[i]+0                                                     #否则认为d所加上的值为0
        if i >= l:                                                           #当i的值大于l时
            d[i]=d[i]-y[i-l]                                                #继续进行d的合成
        else:
            d[i]=d[i]+0                                                     #否则则认为剩余部分为0
        if i >= k+l:                                                         #当i的值大于k+l的情况下
            d[i]=d[i]+y[i-k-l]                                              #进行d的最后计算
        else:
            d[i]=d[i]+0                                                     #否则将d进行保持
    
        #进行P值的计算
        if i == 0:                                                          #在确定为对第一个p进行计算时
            p.append(d[i])                                                  #此时p(i-1)为0，则直接等于d[0]
        else:
            p.append(p[i-1]+d[i])                                           #使用计算得到的d值进行p值的计算
        
        #进行S值的计算
        if i == 0:                                                          #对第一个s值进行计算
            s.append((1+M)*d[i])                                             
        else:
            s.append(s[i-1]+p[i-1]+(1+M)*d[i])                              #对s值的计算方法
        
    for i in range(0,len(s)):                                               #对最终计算出的sn进行归一化
        s[i]=s[i]/(k*M)

    return s,p,d                                                            #返回最终计算出的s列表,p列表和d列表

其中$y$变量为输入的采集脉冲信号，$k,l,m$三个变量分别为$k,l,M$三个参数的选定值，由此便能够完成梯形成型的计算。
为了证明程序的可用性，在此给出调试代码(Note:在调试代码中需要事先安装了matplotlib库，并且将前面的calculateshape函数放置在同一路径下的trapeze_shaper.py文件中)：

import math
import matplotlib.pyplot as plt
import random
from trapeze_shaper import calculateshape                                   #导入梯形成型计算模块

plt.rcParams['font.sans-serif']=['SimHei']                                  #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False                                    #用来正常显示负号

k=20                                                                        #用于确定梯形的上升沿长度为20个采样周期
l=50                                                                        #用于确定平顶的长度为二十个采样周期
M=20                                                                        #给出实际的衰减时间常数
M1=20                                                                       #信号衰减时间常数

MAX_AMP=255                                                                 #考虑到能够产生的最大幅度位于255处

#此部分用于产生负指数信号数据
x1=list(range(0,256))                                                       #产生X轴坐标数据
y1=[]                                                                       #为y留出空位
for num in x1:
  if num < 50:
      y1.append(0)
  else:
      y1.append(math.exp((50-num)/M1))                                    #创建y的函数

for i in range(0,len(y1)):                                                  #使y的最大值达到255
  y1[i]=int(MAX_AMP*y1[i])+random.randint(-10, 10)                        #给出y的相应值


plt.figure("带噪声单信号梯形成型")                                           #给出第一个绘图窗口
s1,p1,d1=calculateshape(y1,k,l,M)                                                 #调用函数，根据y1产生s1,p1,d1
ax1=plt.subplot(3,1,1)
ax1.plot(x1,y1,label='原始单一单指数信号')                                   #画出原始波形
ax1.plot(x1,s1,label='梯形成型后波形')                                       #创建完成梯形成型后的图形
ax1.set_ylabel("幅度(LSB)")
ax1.legend()


ax2=plt.subplot(3,1,2)                                                      #给出该梯形成型过程中的中间变量pn
ax2.plot(x1,p1,label="p(n)")
ax2.set_ylabel("p(n)")
ax2.legend()                                                 

ax3=plt.subplot(3,1,3)
ax3.plot(x1,d1,label="d(n)")
ax3.set_xlabel('时间(t)')
ax3.set_ylabel('d(n)')
ax3.legend()

plt.show()

以上代码首先产生了一个经过离散化后衰减时间常数为$M=20$的负指数信号，并引入了一些噪声，再调用梯形成型函数，同样设置参数$M=20$,且令$k=20,l=50$，由此的到成型梯形如下图：

其中最上面部分显示了产生的负指数脉冲信号，以及完成后的信号结果，下面两图分别显示了$p[n]$和$d^{k,l}[n]$的计算结果，可见通过该算法能够在尽可能少的使用除法和指数运算的条件下完成梯形成型。

小结

在本文中简单对负指数信号的处理方法进行了介绍，并重点给出了利用函数卷积法完成梯形成型的数学原理$(24)\sim (26)$，并给出了在计算机中的计算程序和结果。但实际上这一算法主要是针对FPGA适应Verilog HDL等并行式运行的语言而产生，在此受限于篇幅未进行给出，不过笔者已经完成相应的设计(主要通过延时链完成)和仿真，不过在了解算法的原理后，再进行电路的设计我认为并不存在智力上的过多工作,当然如果实在难以完成也欢迎进行交流讨论。
最后，原创不易，欢迎转载，但请注明出处^_^!