【计算机图形学】二维图形裁剪算法

最新推荐文章于 2024-10-04 01:50:18 发布

intm_

最新推荐文章于 2024-10-04 01:50:18 发布

阅读量4.2k

点赞数 6

分类专栏：计算机图形学文章标签：算法 python 图形渲染

本文链接：https://blog.csdn.net/print_gqh/article/details/129121940

版权

计算机图形学专栏收录该内容

3 篇文章

订阅专栏

一. 线段裁剪

Cohen-Sutherland算法

Cohen-Sutherland是最早最流行的算法。

核心思想：通过编码测试来减少计算交点的次数。（编码算法）

1. 区域码：

线段端点以区域赋值以四位二进制码。

编码顺序：四位从右到左分别为：左边界、右边界、下边界、上边界。
编码值：落在相应位置为1，否则为0
如图：
求区域码：可以通过将坐标与四个边界比较，也可以通过做减法看符号位。

2. 算法流程及代码

算法流程：
线段位置一共有3种情况：完全在窗口内、完全在窗口外、部分在窗口内
根据线段端点的区域码快速判断：
- C1 | C2=0: 表示两个端点区域码都为0000，线段在窗口内，直接返回。（如P5P6）
- C1 & C2 !=0: 表示两个端点区域码有同样的位置都为1，完全在窗口外，全部舍弃，返回。(如P9P10)
- 不能确定完全在窗口内外的线段–>求交(如P1P2、P3P4、P7P8)
  - 方法是：首先对线段外端点（落在窗口外的点）与一条裁剪边界比较来确定需要裁剪多少线段；然后，将线段的剩下部分与其他裁剪边界对比，直到该直线完全落在窗口内或者被舍弃。
  - 要点：始终保证P1为落在窗口外的点，将P1与窗口边界求交。

代码；

def Cohen-Sutherland(p_list, x_min, y_min, x_max, y_max):
"""线段裁剪
:param p_list: (list of list of int: [[x0, y0], [x1, y1]]) 线段的起点和终点坐标
:param x_min: 裁剪窗口左上角x坐标
:param y_min: 裁剪窗口左上角y坐标
:param x_max: 裁剪窗口右下角x坐标
:param y_max: 裁剪窗口右下角y坐标
:return: (list of list of int: [[x_0, y_0], [x_1, y_1]]) 裁剪后线段的起点和终点坐标
"""
    result = []
    if y_min > y_max:
        y_min, y_max = y_max, y_min
    x0, y0 = p_list[0]
    x1, y1 = p_list[1]

    while 1:
        code0 = 0 #1_left, 2_right, 4_down, 8_up
        code1 = 0 #1_left, 2_right, 4_down, 8_up
        #calc code0
        if x0 < x_min:
            code0 += 1
        elif x0 > x_max:
            code0 += 2
        if y0 < y_min:
            code0 += 4
        elif y0 > y_max:
            code0 += 8
        #calc code1
        if x1 < x_min:
            code1 += 1
        elif x1 > x_max:
            code1 += 2
        if y1 < y_min:
            code1 += 4
        elif y1 > y_max:
            code1 += 8
        #inside
        if (code0 | code1) == 0:
            result = [[x0, y0], [x1, y1]]
            break
        #outside
        elif (code0 & code1) != 0:
            result.append([0,0])
            result.append([0,0])
            break
        #otherwise
        else:
            if code0 == 0:
                x0, x1 = x1, x0
                y0, y1 = y1, y0
                code0, code1 = code1, code0
            #1_left, 2_right, 4_down, 8_up
            if (code0 & 1):
                y0 = int(y0 + ((x_min-x0) * (y0-y1)/(x0-x1)) + 0.5)
                x0 = x_min
            if (code0 & 2):
                y0 = int(y0 + ((x_max-x0) * (y0-y1)/(x0-x1)) + 0.5)
                x0 = x_max
            if (code0 & 4):
                x0 = int(x0 + ((y_min-y0) * (x0-x1)/(y0-y1)) + 0.5)
                y0 = y_min
            if (code0 & 8):
                x0 = int(x0 + ((y_max-y0) * (x0-x1)/(y0-y1)) + 0.5)
                y0 = y_max
	return result

3. 三维空间中的cohen-Sutherland算法

利用6位区域码
必要时利用平面进行线段裁剪

4. 拓展：将Cohen-Sutherland改进为外裁剪算法

上述Cohen-Sutherland算法主要用于进行内裁剪，即保留位于窗口内的二维图形，那么如果想要进行外裁剪，即保留窗口外的二维图形呢？

此处改进算法是我自己的思考，不能保证完全正确：

请添加图片描述

直线与窗口的位置关系可以分为4类：
- C1 | C2 =0: 即完全在窗口内（如P5P6），直接舍去
- C1 & C2 !=0: 存在相同的位置上都为1，即完全在窗口外且在同一区域（如P9P10），直接返回
- C1==0 ｜ C2= =0: 即一个端点在窗口内（如P7P8），取在窗口外的端点与窗口求交（求交方法与Cohen-Sutherland一样），只需一次得到交点，交点与外端点之间的线段即所求，返回。
- 剩下的情况：两个端点都在窗口外且不在同一区域，无法确定（如P1P2、P3P4），取其中一个端点与窗口求交，得到交点与另一端点构成的线段，判断线段是否完全在窗口外，是则舍弃，返回；不是则变成第3种情况。

Liang-Barsky算法：

核心思想：将二维裁剪变成一维问题。
设P1P2所在的直线为L，直线或其延长线与窗口的交点为Q1Q2，Q1Q2称为诱导窗口，它是一维的。
P1P2关于二维窗口的裁剪结果与P1P2关于诱导窗口的裁剪结果是一致的。

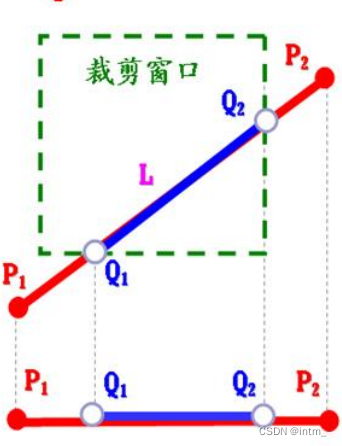
1. 直线的参数方程

请添加图片描述
u=0时，为P1；u=1时，为P2。

2. 入边和出边

定义：
- 入边：直线由窗口外向窗口内移动时和窗口边界相交的边（左边界和下边界）。
- 出边：直线由窗口内向窗口外移动时和窗口边界相交的边（右边界和上边界）。
如何确定入边和出边
首先，将线段看作矢量（方向为P1->P2，即和参数方程一致），线段与窗口首先相交的两条边为入边，后相交的两条边为出边。
例如，如上图，当u从-∞到+∞遍历直线时，首先对裁剪窗口的两条边界直线（下边和左边）从外面向里面移动，再对裁剪窗口两条边界直线（上边和右边）从里面向外面移动。因此入边为窗口下边和左边，出边为窗口上边和右边。
由参数方程和不等式判断入边和出边
根据窗口边界，可以确定裁剪后的线段必定满足以下两行不等式：

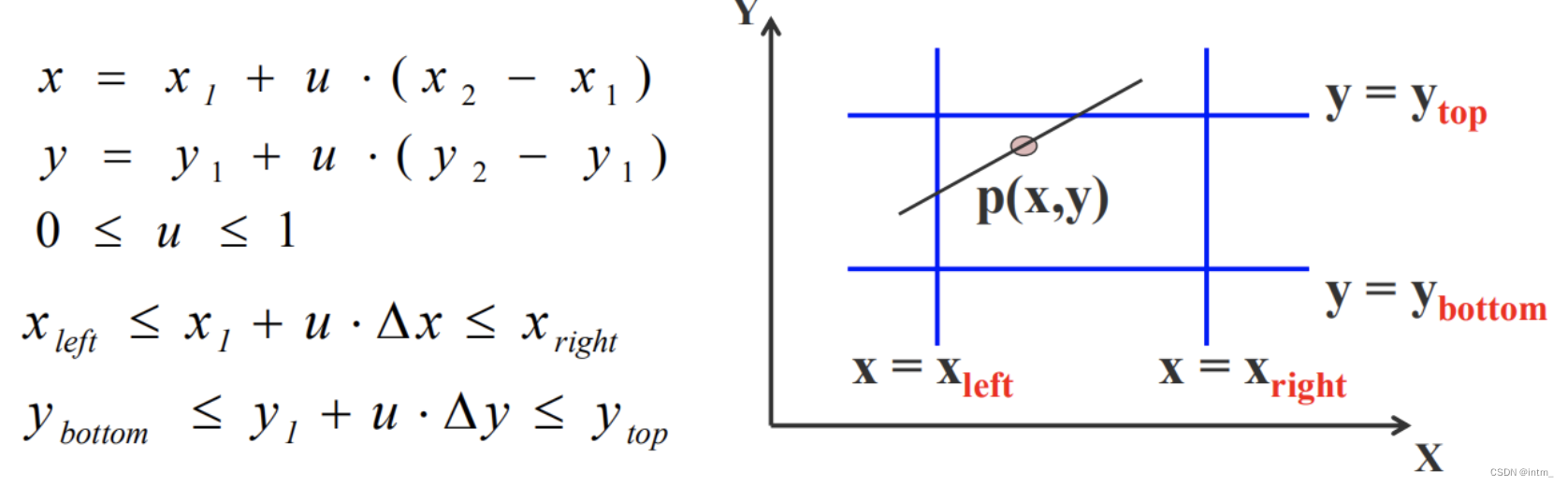
变形后可得：

此时可以根据pk的正负来判断入边和出边：
- pk<0: 入边，可得线段与入边的交点处对应的参数为u=pk/qk
- pk>0: 出边
- 若pk==0且qk<0：线段完全在窗口外，直接舍弃

请添加图片描述

3. 裁剪算法结果

设裁剪后线段的左右边界为u_min,u_max。
则 $\begin{cases} u_{min}=max(u_0,u_{入边1}，u_{入边2})\\u_{max}=min(u_1,u_{出边1}，u_{出边2}) \end{cases}$
若u_min>u_max，则直线段在窗口外，直接舍弃
若u_min<=u_max，带回参数方程可得裁剪后线段的两个端点。

4. 代码实现

def Liang-Barsky(p_list, x_min, y_min, x_max, y_max):
    """线段裁剪

    :param p_list: (list of list of int: [[x0, y0], [x1, y1]]) 线段的起点和终点坐标
    :param x_min: 裁剪窗口左上角x坐标
    :param y_min: 裁剪窗口左上角y坐标
    :param x_max: 裁剪窗口右下角x坐标
    :param y_max: 裁剪窗口右下角y坐标
    :return: (list of list of int: [[x_0, y_0], [x_1, y_1]]) 裁剪后线段的起点和终点坐标
    """
    result = []
    if y_min > y_max:
         y_min, y_max = y_max, y_min
     x0, y0 = p_list[0]
     x1, y1 = p_list[1]

     p = [x0 - x1, x1 - x0, y0 - y1, y1 - y0]
     q = [x0 - x_min, x_max - x0, y0 - y_min, y_max - y0]
     u0, u1 = 0, 1

     for i in range(4):
         if p[i] < 0:
             u0 = max(u0, q[i] / p[i])
         elif p[i] > 0:
             u1 = min(u1, q[i] / p[i])
         elif (p[i] == 0 and q[i] < 0):
             result = [[0, 0], [0, 0]]
             return result
         if u0 > u1:
             result = [[0, 0], [0, 0]]
             return result
     res_x0=0
     res_y0=0
     res_x1=0
     res_y1 = 0
     if u0 > 0:
         res_x0 = int(x0 + u0 * (x1 - x0) + 0.5)
         res_y0 = int(y0 + u0 * (y1 - y0) + 0.5)
     if u1 < 1:
         res_x1 = int(x0 + u1 * (x1 - x0) + 0.5)
         res_y1 = int(y0 + u1 * (y1 - y0) + 0.5)
     result = [[res_x0, res_y0], [res_x1, res_y1]]

    return result

5. 拓展：将Liang-Barsky算法改进为外裁剪算法

个人思考，不保证准确！：

前面流程不变，最后只需要将内裁剪算法得到的[u_min, u_max]在[0,1]区间中求补集。

Nicholl-Lee-Nicholl算法(NLN)

主要思想：
在裁剪窗口中周围创建多个区域以进行更多的区域测试 --> 避免对一个多线段进行多次裁剪 --> 减少求交计算

比上面那两个算法的除法和减法次数少
仅适用于二维

1. 区域划分

共有四种情况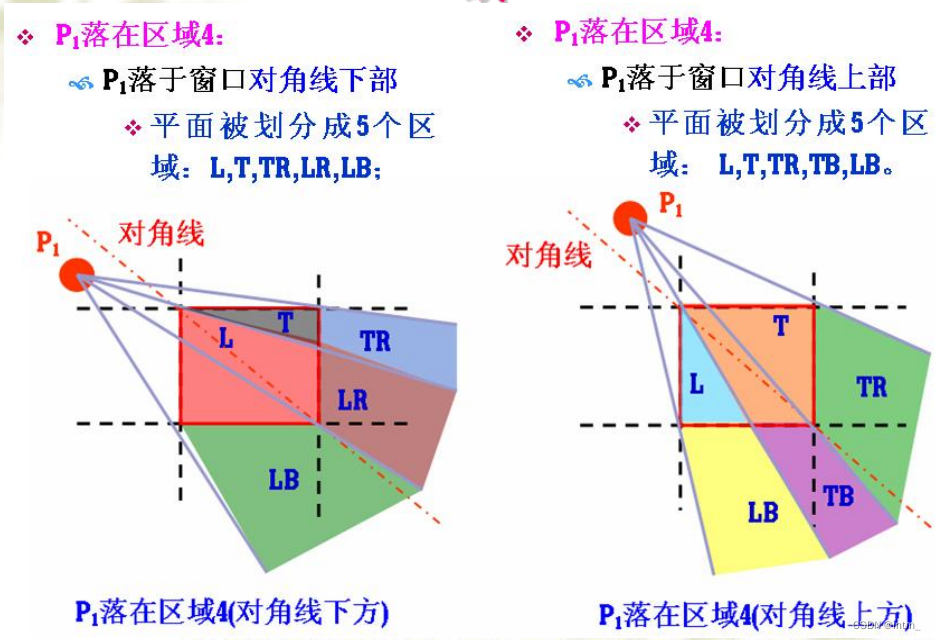：请添加图片描述

请添加图片描述

2. 确定另一顶点所在区域

采用斜率判断、坐标判断、参数方程判断···（不管什么方法，判断出来就行）
请添加图片描述

二. 多边形裁剪

采用线段裁剪算法对多边形进行裁剪

线段裁剪算法对多边形进行裁剪所要考虑的问题：

多边形的定义，即：多边形各组成边的关系
- 凸多边形：用线段裁剪处理的凸多边形边界显示为一系列不连接的直线段；即：多边形的边被裁剪后一般不再封闭，需要用窗口边界的适当部分来封闭它。如何确定这部分边界？
- 凹多边形：可能被裁剪成几个小多边形。如何确定这些小多边形的边界？

请添加图片描述

Sutherland-Hodgman算法（萨瑟兰-霍奇曼算法）

Sutherland-Hodgman算法也叫逐边裁剪法，该算法是萨瑟兰德(I．E．Sutherland)和霍德曼(Hodgman)在1974年提出的。这种算法采用了分割处理、逐边裁剪的方法。

1. 两个空间

裁剪窗口边界所在直线将二维空间分成两个半空间：内侧空间和外侧空间

2. 算法流程

对多边形顶点集初始化排序（顺时针或者逆时针）
定义一个输出顶点表，初始化为空
按照边顺序依次裁剪
按照边与窗口的关系将相应点保存至顶点表
- 保存规则：
按照一开始顶点规定的顺序（顺时针或逆时针）连接输出顶点表

3. 伪代码

   List outputList = subjectPolygon;  
   
   for (Edge clipEdge in clipPolygon) do
      List inputList = outputList;
      outputList.clear();
    
      for(int i = 0 ; i < inputList.count ; i += 1) do
         Point current_point = inputList[i];
         Point prev_point = inputList[(i + inputList.count - 1) % inputList.count];
    
         Point Intersecting_point = ComputeIntersection(prev_point, current_point, clipEdge)
    
         if (current_point inside clipEdge) then
            if (prev_point not inside clipEdge) then
               outputList.add(Intersecting_point);
            end if
            outputList.add(current_point);
         
         else if (prev_point inside clipEdge) then
            outputList.add(Intersecting_point);
         end if
    
      done
   done

4. 算法缺陷

Sutherland-Hodgman 裁剪算法对凹多边形进行裁剪可能出现多余的线；这种情况在裁剪结果多边形有两个或多个分离部分时会出现。
成因：
- 只有一个输出顶点表；
- 且结果多边形的最后一个顶点总是与其第一个顶点相连。
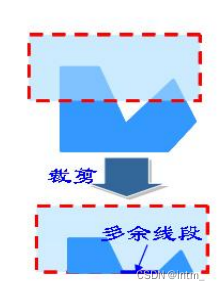
裁剪凹多边形的改进算法
- 将凹多边形分割成多个凸多边形
- Weilerr-Atherton算法：更常用的多边形算法

Weilerr-Atherton算法

1. 两个顶点表

初始化两个顶点表，分别为多边形顶点表和裁剪窗口顶点表（顺时针）
求出所有交点，并将这些交点按顺序插入两个顶点表中
在两个顶点表之间的相同点处建立双向指针（具体算法，为了过程中好找点，此处不理解可以接着看下面的算法流程）

2. 算法流程

假设被裁剪多边形和裁剪窗口的顶点序列都按顺时针方向排列。当两个多边形相交时，交点必然成对出现，其中一个是从被裁剪多边形进入裁剪窗口的交点，称为入点，另一个是从被裁剪多边形离开裁剪窗口的交点，称为出点。
算法从被裁剪多边形的一个入点开始，碰到入点，沿着被裁剪多边形按顺时针方向搜集顶点序列；
而当遇到出点时，则沿着裁剪窗口按顺时针方向搜集顶点序列。
按上述规则，如此交替地沿着两个多边形的边线行进，直到回到起始点。这时，收集到的全部顶点序列就是裁剪所得的一个多边形。

由于可能存在分裂的多边形，因此算法要考虑：将搜集过的入点的入点记号删去，以免重复跟踪。将所有的入点搜集完毕后算法结束。

如下图：

具体流程解释可以学习:多边形裁剪二：Weiler-Atherton算法

请添加图片描述

参考博客：

[1] https://blog.csdn.net/weixin_44397852/article/details/109015504
[2] https://www.cnblogs.com/wkfvawl/p/12083197.html
[3] https://zh.wikipedia.org/zh-hans/%E8%90%A8%E7%91%9F%E5%85%B0-%E9%9C%8D%E5%A5%87%E6%9B%BC%E7%AE%97%E6%B3%95
[4] https://blog.csdn.net/yangxi_pekin/article/details/37738219