第一部分复习

1,
u,v,w表示非零的七维向量,那么他们生成的子空间可能是1,2,3维空间.

2,

一个5×3的上三角矩阵,记为U,并且它的秩=3,那么矩阵U的零空间只有一个0向量.因为秩等于3,有刚好三列,表示这三个列向量线性无关,所以只有0向量可以使其线性组合等于0.N(U)=[0,0,0],这里注意并不是[0,0,0,0,0],列向量才是五维向量,0空间向量与x数量保持一致.

3,

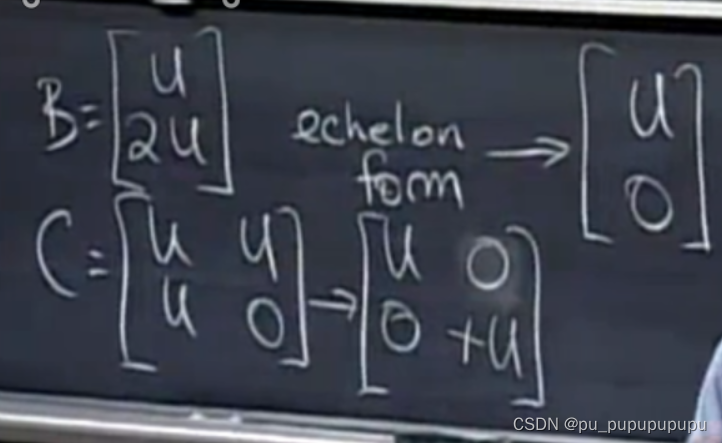
如果将B和C化简成行最简矩阵,结果如上图.如果U(10×3阶矩阵)的秩为3,则B的秩为3,C的秩为6.那么C的左零空间为4维,可以不转置用行数直接减去秩,也可以转置之后用列数减去秩.其实第二种方法更好理解.

4,

如果我们知道结果就可以知道A的形状为3×3,从[2,4,2]有三行可以看出A有3行,从x有三行可以看出A有三列.
那么矩阵A如何求出
首先从特解可以看出,X只有第一个元素为2,对应于A的第一列,表示只有A的第一列参与运算,所以A的第一列为[1,2,1],由通解(AX=0)可以看出第一列加第二列为0向量,第三列只能为0向量,所以

另一个问题,当B为何值时,AX=B有解,其实问的就是A的列空间,从A矩阵很容易看出形成的列空间就是[1,2,1]的任意倍数
5,
如果所有的5×5矩阵组成一个矩阵空间,那么其中可逆矩阵能否构成一个子空间?不可以,首先,0矩阵不包含在内,其次,两个可逆矩阵相加,结果也不一定可逆.

6,方阵B的平方为0,那么能否推出B为0矩阵.

7,

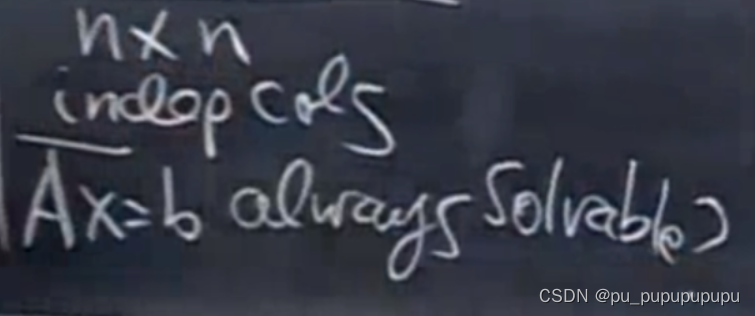
n×n阶方阵,如果是满秩的情况,AX=B是否总是有解的?
是的,简单的理解方法就是,n个n维向量如果线性无关,就可以表述出n维空间中的所有.
第二种,AX=B出现无解的情况,只有在出现0行的时候.

8,

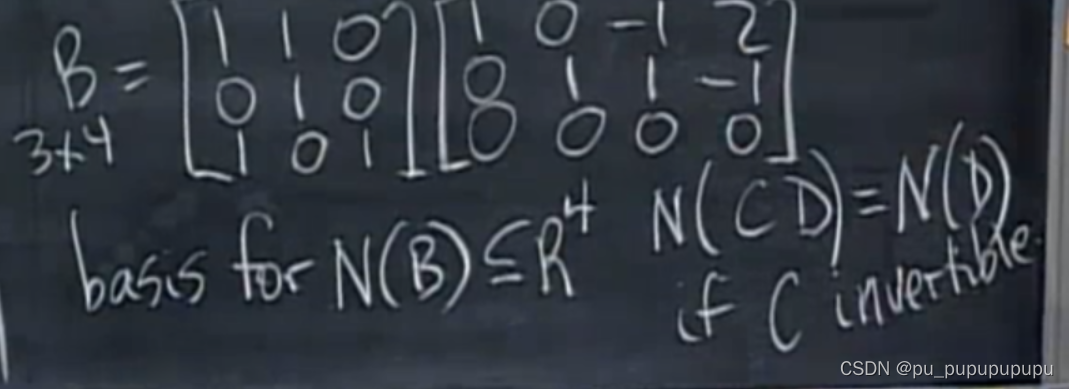
这道题需要求B矩阵的0空间.由于第一个矩阵是可逆的,所以CD的0空间就等于D的0空间.因为总可以左乘C的逆得到0矩阵.
结果如下

由于矩阵为R,所以当然可以直接看出特殊解-F.

在此基础上求BX=[1,0,1]的解,只需要知道一个特解就可以了.
B的第一列就是[1,0,1],所以特解为[1,0,0,0],如何知道第二个特解呢?很简单,第一个特解加通解中的一个,就又得到了一个特解.

9,
如果A为方阵,那么它的行空间与列空间相同吗?
不相同.如果方阵为对称矩阵,那么行空间和列空间相同,因为向量都一样了.

A矩阵与-A是否有相同的四个基本子空间?
是的

如果A与B有相同的基本子空间,那么A是B的倍数?
不是,任何一个6×6的可逆矩阵,行空间与列空间都为R6,但是这六个向量可以不同.

那么如果A与B有相同的四个基本子空间,可以得到什么性质呢
最起码秩是相同的.

10,
如果我交换A的两行,那么什么空间不变?
行空间与零空间不变.因为x看成列的线性组合,是整体进行的,所以不影响0空间.

11,

0空间向量不能是行向量中的一个,因为这样必不可能得到0.
可以这么说,行空间与0空间的交集只有0向量.即行空间与0空间正交.