洛谷 P8815 [CSP-J 2022] 逻辑表达式（T3）

P.Space

已于 2024-03-08 16:48:16 修改

阅读量231

点赞数 9

文章标签： c++ CSP-J 2022

于 2023-08-06 16:47:02 首次发布

本文链接：https://blog.csdn.net/pyc0705/article/details/132121831

版权

题目传送门

[CSP-J 2022] 逻辑表达式 - 洛谷https://www.luogu.com.cn/problem/P8815

算法解析

首先要说一下这种题的通用解题思路：

中缀表达式转后缀表达式
后缀表达式转表达式树
对表达式树进行 dfs

先说一下什么是中缀表达式、后缀表达式、表达式树

首先，中缀表达式就是我们正常写的表达式，比如

1 & (0 | 1 & 0)

后缀表达式呢，就比如上面那个中缀的后缀就是：

1 0 1 0 & | &

什么意思呢，看一眼下图就明白了

_ 代表他连着的两个蓝线中第一个和第二个用 _ 下边的 ∪ 连着的运算符运算上，蓝线连着 ∪ 代表那个 ∪ 的运算结果

为什么要把中缀转后缀呢，因为后缀没有括号，这样扫描一遍就能求出值了

表达式树呢，首先它的中序遍历就是中缀表达式，它的后序遍历就是后缀表达式

什么是中序遍历和后序遍历呢，中序就是“左根右”，后序就是“左右根”

比如下面这棵树：

下图为该树的中序遍历（中缀表达式）

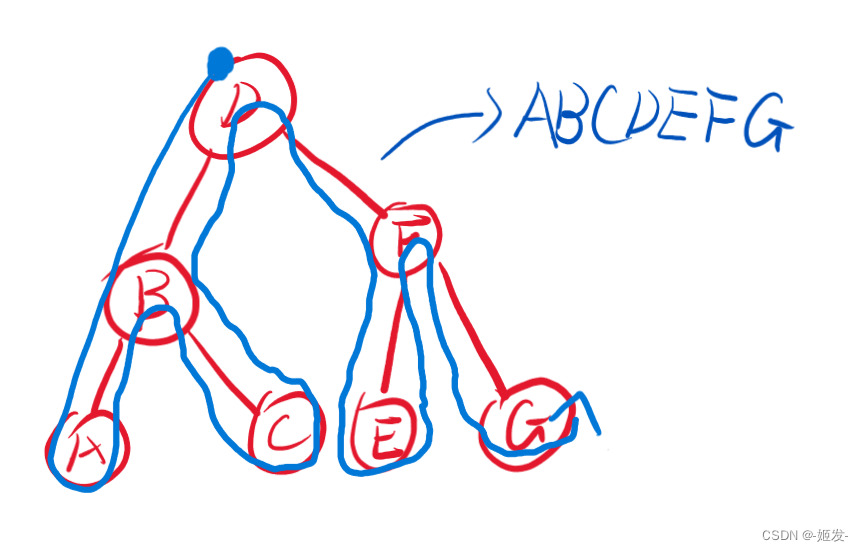
下图为该树的后序遍历（后缀表达式）

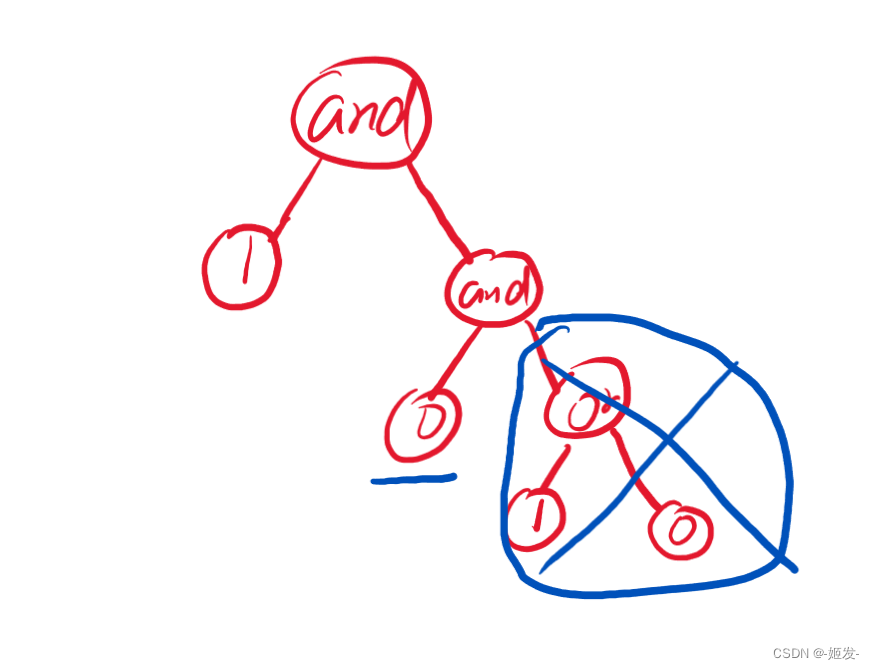
为什么要把后缀转表达式树呢，因为这样好判断短路

他一个节点的结果就是它的左子树运算上它的右子树，运算符为它本身

所以只要它本身是 '&' 并且他左子树的结果是 0，那么就是一次 and 的短路

他本身是 '|' 并且他左子树的结果是 1，那么就是一次 or 短路

比如下边的这棵树

他短路后是这样的

中缀转后缀

那么我们现在就说一下中缀怎么转后缀

首先，要维护一个栈
然后从头到尾遍历整个中缀表达式
如果是数字，直接输出
如果是运算符，弹出栈顶所有优先级大于等于该运算符的运算符，最后将该字符压栈
如果是左括号，压栈
如果是右括号，一直弹栈，直到栈顶为左括号

栈，我们可以用 STL中的 stack

stack <char> st;

然后，我们就需要执行遍历整个中缀表达式了

for(int i = 0; i < infix.size(); ++i)

然后我们依次判断如果他是什么，就做什么

首先是数字，这里可以用 isdigit，他需要头文件

#include <cctype>

然后看如果他是数字，就直接输出到后缀，然后 continue 掉

这里我后缀用的是 vector 来存储

if(isdigit(infix[i])) {
	suffix.push_back(infix[i]);
	continue;
}

然后就是看如果他是左括号，压栈，然后 continue 掉

if(infix[i] == '(') {
	st.push(infix[i]);
	continue;
}

如果他是右括号，就一直弹栈，直到栈顶为左括号，注意，最后也要把左括号弹掉

if(infix[i] == ')') {
	while(st.top() != '(') {
		suffix.push_back(st.top());
		st.pop();
	}
	st.pop();
	
	continue;
}

最后，就剩下运算符了，分别把栈顶所有优先级大于等于它的都弹掉，最后将自己压栈

while(infix[i] == '&' && !st.empty() && st.top() == '&') {
	suffix.push_back(st.top());
	st.pop();
}

while(infix[i] == '|' && !st.empty() && (st.top() == '|' || st.top() == '&')) {
	suffix.push_back(st.top());
	st.pop();
}

st.push(infix[i]);

记得最后要把栈中剩余的全部弹掉：

while(!st.empty()) {
	suffix.push_back(st.top());
	st.pop();
}

我们测试一下：

for(auto p : suffix)
	cout << p << " ";

这其实就是一种特殊的遍历方法，等于

for(int i = 0; i < suffix.size(); ++i) {
	auto p = suffix[i];
    cout << p << " ";
}

结果：

OK，对了！

后缀转表达式树

下一步就是后缀转表达式树了，先说一下怎么转

建立结点结构体
维护一个栈
遍历整个后缀表达式
碰到数字，生成一个值为本身的结点，压栈
碰到运算符，生成一个运算符结点，取出栈顶两个结点，分别为该结点的左孩子和右孩子，压栈
最后栈中肯定剩一个结点，把它设为根结点

好，我们先建立一个结点结构体，可以用指针记录它的左孩子和右孩子

还可以用 op 记录它是否是数字（是数字就是 '$' ，不是数字则是它本身）

还需要记录以它为根结点的树的值，val

可以用一个构造函数，参数为一个字符（数字或运算符），然后看它如果是数字，就把 op 赋成 '$'，val 赋成它减 48（变成数字，字符 '0' 的 ASCII 码为 48），否则就是字符，将 op 赋成它本身

struct Node {
	Node *le, *rt;
	char op;
	bool val;
	
	Node(char _op) {
		if(isdigit(_op)) {
			op = '$';
			val = _op - 48;
		} else {
			op = _op;
		}
	}
} *root;

然后就是维护一个栈

stack <Node*> st;

现在遍历整个后缀

for(auto ch : suffix)

然后碰到数字就生成一个值为本身的结点，压栈

if(isdigit(ch))
	st.push(new Node(ch));

否则就生成一个运算符结点，取出栈顶两个结点，分别为该结点的左子树和右子树，压栈

else {
	Node *p = new Node(ch);
	Node *le = st.top();
	st.pop();
	Node *rt = st.top();
	st.pop();
	p->le = le;
	p->rt = rt;
	
	st.push(p);
}

最后就是将根结点设为栈顶结点了

root = st.top();

OK！搞定！\(^o^)/~

（其实这道题如果只要求输出值，就不用建树了，直接遍历后缀表达式，碰见数字就压栈，碰见运算符就将栈顶两个数字弹出，然后用现在的运算符运算上，结果再压栈就可以了，其实和建表达式树的过程是一样的）

对表达式树进行 dfs

最后我们就要开始对表达式树进行 dfs 了

首先要确定参数，可以是当前遍历到的结点

bool dfs(Node *x)

这样，刚开始就要传进去根结点

dfs 可以有一个返回值，记录结果

这样直接输出就可以了

cout << dfs(root) << endl;

先判断如果是数字，直接返回他的值

if(x->op == '$')
    return x->val;

否则的话（运算符），它就返回左孩子运算上右孩子，运算符为它的 op

可以在这个时候记录短路

bool le = dfs(x->le);
if(le == 1 && x->op == '|') {
	++cnt_or;
	return 1;
}
if(le == 0 && x->op == '&') {
	++cnt_and;
	return 0;
}
bool rt = dfs(x->rt);
if(x->op == '|')
	return le || rt;
return le && rt;

最终代码

最终代码如下：

#include <iostream>
#include <string>
#include <vector>
#include <stack>
#include <cctype> 
using namespace std;

struct Node {
	Node *le, *rt;
	char op;
	bool val;
	
	Node(char _op) {
		if(isdigit(_op)) {
			op = '$';
			val = _op - 48;
		} else {
			op = _op;
		}
	}
};

Node *root;
string infix;
vector <char> suffix;
int cnt_and, cnt_or;

void inp() {
	cin >> infix;
}

void build_suffix() {
	stack <char> st;
	for(int i = 0; i < infix.size(); ++i) {
		if(isdigit(infix[i])) {
			suffix.push_back(infix[i]);
			
			continue;
		}
		
		if(infix[i] == '(') {
			st.push(infix[i]);
			
			continue;
		}
		
		if(infix[i] == ')') {
			while(st.top() != '(') {
				suffix.push_back(st.top());
				st.pop();
			}
			st.pop();
			
			continue;
		}
		
		while(infix[i] == '&' && !st.empty() && st.top() == '&') {
			suffix.push_back(st.top());
			st.pop();
		}
		
		while(infix[i] == '|' && !st.empty() && (st.top() == '|' || st.top() == '&')) {
			suffix.push_back(st.top());
			st.pop();
		}
		
		st.push(infix[i]);
	}
	
	while(!st.empty()) {
		suffix.push_back(st.top());
		st.pop();
	}
}

void build_tree() {
	stack <Node*> st;
	for(auto ch : suffix) {
		if(isdigit(ch))
			st.push(new Node(ch));
		else {
			Node *p = new Node(ch);
			Node *rt = st.top();
			st.pop();
			Node *le = st.top();
			st.pop();
			p->le = le;
			p->rt = rt;
			
			st.push(p);
		}
	}
	root = st.top();
}

bool dfs(Node *x) {
	if(x->op == '$')
		return x->val;
	
	bool le = dfs(x->le);
	if(le == 1 && x->op == '|') {
		++cnt_or;
		return 1;
	}
	if(le == 0 && x->op == '&') {
		++cnt_and;
		return 0;
	}
	bool rt = dfs(x->rt);
	if(x->op == '|')
		return le || rt;
	return le && rt;
	
}

void work() {
	build_suffix();
	build_tree();
	cout << dfs(root) << endl;
	cout << cnt_and << " " << cnt_or << endl;
}

int main() {
	inp();
	work();
	
	return 0;
}