这篇博客探讨了回归树在处理连续目标特征时的作用，对比了分类树的差异。文章介绍了回归树的生长原理，包括使用方差作为分割标准，以及在Python中构建回归树的步骤。通过UCI共享单车数据集的示例，展示了如何应用和评估回归树模型，同时提到了sklearn库中的DecisionTreeRegressor实现。
在上一章关于分类决策树的章节中，我们介绍了决策树模型的基本概念，如何使用 Python 从头开始构建它们，以及使用预先打包的 sklearn DecisionTreeClassifier 方法。我们还介绍了决策树模型的优缺点以及重要的扩展和变体。分类决策树的一个缺点是它们需要一个分类缩放的目标特征，例如天气 = {晴天、雨天、阴天、雷雨}。
这里出现了一个问题：例如，如果我们希望我们的树根据房间数量和位置等一些目标特征属性来预测房屋的价格，该怎么办？这里目标特征（奖品）的值不再按类别缩放，而是连续的——理论上，房子可以有无数种不同的价格——
这就是回归树的用武之地。回归树的工作原理与分类树相同，区别在于目标特征值现在可以采用无限数量的连续缩放值。因此，现在的任务是在给定一组分类（或连续）缩放的描述性特征 X 的值的情况下预测连续缩放的目标特征 Y 的值。
如上所述，构建回归树的原理与创建分类树的方法相同。
我们搜索最纯粹地分割目标特征值的描述性特征，沿着这个描述性特征的值划分数据集，并对每个子数据集重复这个过程，直到我们完成一个停止标准。如果我们完成一个停止标准，我们生长一个叶子节点。
尽管如此，一些事情发生了变化。
首先，让我们考虑一下我们在分类树章节中介绍的用于生长叶节点的停止标准：
- 如果拆分过程导致空数据集，则返回原始数据集的模式目标特征值
- 如果分裂过程导致没有特征的数据集，则返回直接父节点的模式目标特征值
- 如果拆分过程导致目标特征值纯的数据集，则返回此值
如果我们现在考虑新的连续缩放目标特征的属性，我们会提到不能再使用第三个停止标准，因为目标特征值现在可以采用无限数量的不同值。因此，在数据集中只剩下一个实例之前，我们很可能不会找到纯目标特征值。
长话短说，一般来说没有什么比纯目标特征值更好的了。
为了解决这个问题，我们将引入一个提前停止标准，如果数据集中的实例数为 ≤5.
通常，在处理回归树时，我们将返回平均目标特征值作为叶节点的预测。
当我们考虑拆分过程本身时，我们必须进行的第二个更改变得明显。
在使用分类树时，我们使用特征的信息增益 (IG) 作为分割标准。也就是说，使用具有最大 IG 的特征来分割数据集。考虑以下示例，其中我们仅检查一个描述性特征，例如卧室数量和作为目标特征的房屋成本。
将 熊猫 导入为 pd
将 numpy 导入为 np
df = pd 。数据帧（{ 'Number_of_Bedrooms' ：[ 2 ，2 ，4 ，1 ，3 ，1 ，4 ，2 ]，'Price_of_Sale' ：[ 100000 ，120000 ，250000 ，80000 ，220000 ，170000 ，500000 ，75000 ]}）
DF
现在我们如何计算Number_of_Bedrooms特征的熵？
H(N你米乙电子r ○F 乙电子dr○○米秒)=∑j ∈ N你米乙电子r ○F 乙电子dr○○米秒＊(|DN你米乙电子r ○F 乙电子dr○○米秒=j||D|＊(∑克 ∈ 磷r一世C电子 ○F 秒一个升电子＊(-磷(克 | j)＊升○G2(磷(克 | j)))))
如果我们计算加权熵，我们会看到对于 j = 3，我们得到的加权熵为 0。我们得到这个结果是因为数据集中只有一所房子有 3 间卧室。另一方面，对于 j = 2（出现 3 次），我们将得到 0.59436 的加权熵。
长话短说，由于我们的目标特征是连续缩放的，分类缩放的描述性特征的 IG 不再是合适的分割标准。
好吧，我们可以改为按照其值对目标特征进行分类，例如房价介于$0和之间$80000被归类为低、介于$80001和$150000中以及 >$150001高。
我们在这里所做的是将回归问题转化为分类问题。但是，由于我们希望能够从无限数量的可能值（回归）中进行预测，这不是我们想要的。
让我们回到我们最初的问题：我们想要一个分裂标准，它允许我们以这样的方式分裂数据集，当到达树节点时，预测值（我们将预测值定义为在此叶节点上的实例（我们将 5 个实例的最小数量定义为提前停止标准）最接近实际值。
事实证明，方差是回归树最常用的分割标准之一，我们将使用方差作为分割标准。
因此，解释是，当沿着这些目标特征的值分割数据集时，我们想要搜索最准确地指向真实目标特征值的特征属性。因此，请检查以下图片。您认为Number_of_Bedrooms功能的这两种布局中的哪一种更准确地指向真正的销售奖？
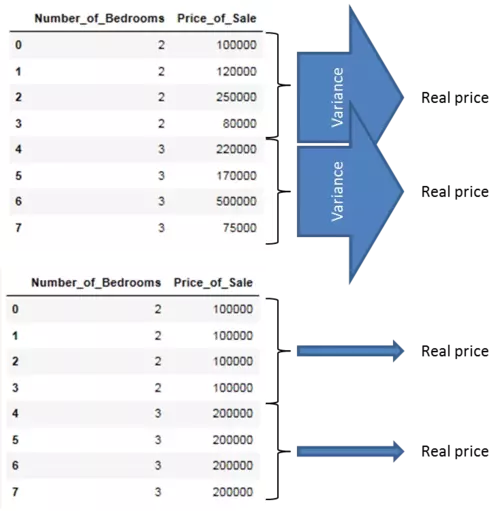
嗯，显然是方差最小的那个！我们将在下一节介绍方差度量背后的数学原理。
目前，我们首先用箭头说明这些，其中宽箭头代表高方差，细箭头代表低方差。我们可以通过显示描述性特征的每个值的目标特征的方差来说明这一点。如您所见，当我们沿着描述性特征的值分割数据集时，最小化目标特征值方差的特征布局是最准确地指向真实值的特征布局，因此应该用作分割标准。在创建回归树模型期间，我们将使用方差度量来代替信息增益作为拆分标准。
回归树背后的数学
如上所述，生长回归树期间的任务原则上与创建分类树期间的任务相同。但是，由于目标特征的连续性，IG 不再是合适的分割标准（基尼指数也不是），我们必须有一个新的分割标准。
因此我们使用我们现在要介绍的方差。
方差
伏一个r(X)=∑一世 =1n(是一世-是¯)n-1
在哪里 是一世 是单个目标特征值和 是¯ 是这些目标特征值的平均值。
以上面的例子为例，Prize_of_Sale目标特征的总方差计算公式为：
=19.903125＊109 #Large Number ;) 虽然这对我们的计算没有影响
由于我们想知道哪个描述性特征最适合分割目标特征，我们必须计算描述性特征的每个值相对于目标特征值的方差。
因此，对于上面的Number_of_Rooms描述性特征，我们得到了单个房间数：
伏一个r(N你米乙电子r ○F 电阻○○米秒 = 1)=(80000-125000)2+(170000-125000)21=4050000000
伏一个r(N你米乙电子r ○F 电阻○○米秒 = 2)=(100000-98333.3)2+(120000-98333.3)2+(75000-98333.3)22=508333333.3
伏一个r(N你米乙电子r ○F 电阻○○米秒 = 3)=(220000-220000)2=0
伏一个r(N你米乙电子r ○F 电阻○○米秒 = 4)=(250000-375000)2+(500000-375000)21=31250000000
由于我们现在还想解决这样一个问题，即存在相对较少出现但具有高方差的特征值（这可能导致整个特征的方差非常高，仅仅因为一个轮廓特征值，即使所有其他特征值的方差特征值可能很小）我们通过计算每个特征值的加权方差来解决这个问题：
宽电子一世GH吨伏一个r(N你米乙电子r ○F 电阻○○米秒 = 1)=28＊4050000000=1012500000
宽电子一世GH吨伏一个r(N你米乙电子r ○F 电阻○○米秒 = 2)=28＊508333333.3=190625000
宽电子一世GH吨伏一个r(N你米乙电子r ○F 电阻○○米秒 = 3)=28＊0=0
宽电子一世GH吨伏一个r(N你米乙电子r ○F 电阻○○米秒 = 4)=28＊31250000000=7812500000
最后，我们总结这些加权方差以对整个特征进行评估：
秒你米伏一个r(F电子一个吨你r电子)=∑v一个升你电子 ∈ F电子一个吨你r电子宽电子一世GH吨伏一个r(F电子一个吨你r电子v一个升你电子)
在我们的情况下：
1012500000+190625000+0+7812500000=9015625000
将所有这些放在一起最终得出加权特征方差的公式，我们将在拆分过程中的每个节点使用该公式来确定我们应该选择下一步拆分数据集的特征。
F电子一个吨你r电子[CH○○秒电子] =精氨酸F ∈ F电子一个吨你r电子秒 ∑升 ∈ 升电子v电子升秒(F)|F=升||F|＊伏一个r(吨,F=升)
=精氨酸F ∈ F电子一个吨你r电子秒 ∑升 ∈ 升电子v电子升秒(F)|F=升||F|＊∑一世 = 1n(吨一世-吨¯)2n-1
这里f表示单个特征，l表示特征的值（例如价格 == 中等），t表示子集中目标特征的值，其中f=l。
按照这个计算规范，我们在每个节点找到特征来分割我们的数据集。
为了说明沿最低方差特征的特征值拆分数据集的过程，我们以UCI 共享单车数据集的简化示例为例，稍后我们将在回归树中使用本章的Python部分从头开始并计算每个特征的方差以找到我们应该用作根节点的特征。
将 熊猫 导入为 pd
df = pd 。read_csv ( "data/day.csv" , usecols = [ 'season' , 'holiday' , 'weekday' , ' weathersit ' , 'cnt' ])
df_example = df 。样本（分数= 0.012 ）
季节
=16429.1
工作日
气象站
由于 Weekday 特征的方差最小，因此该特征用于拆分数据集，因此用作根节点。尽管由于随机抽样，这个例子并不那么健壮（例如没有工作日 == 3 的实例）它应该传达使用方差作为拆分度量的数据拆分背后的概念。
由于我们现在已经介绍了如何使用方差度量来分割具有连续目标特征的数据集的概念，我们现在将调整分类树的伪代码，以便我们的树模型能够处理连续缩放的目标特征值。
如上所述，我们必须进行两项更改才能使我们的树模型能够处理连续缩放的目标特征值：
**1. 我们引入了一个早期停止标准，我们说如果一个节点上的实例数是≤5 （我们可以调整这个值），返回这些数字的平均目标特征值**
**2. 我们使用特征的方差而不是信息增益作为我们新的分割标准**
因此伪代码变为：
ID3(D,Feature_Attributes,Target_Attributes,min_instances=5)
创建根节点 r
将 r 设置为 D #######Changed######## 中目标特征值的平均值
如果 num_instances <= min_instances ：
返回
别的：
经过
如果 Feature_Attributes 为空：
返回
别的：
Att = 来自 Feature_Attributes 的具有最低加权方差的属性 ########Changed########
r = Att
对于 Att 中的值：
在 r 下面添加一个新节点，其中 node_values = (Att == values)
Sub_D_values = (Att == 值)
如果 Sub_D_values == 空：
添加叶节点 l 其中 l 等于 D 中目标值的平均值
别的：
添加带有 ID3 的 Sub_Tree(Sub_D_values,Feature_Attributes = Feature_Attributes without Att, Target_Attributes,min_instances=5)
除了实际算法的变化之外，我们还必须使用另一种准确度度量，因为我们不再处理分类目标特征值。也就是说，我们不能再简单地将预测类别与真实类别进行比较并计算我们命中目标的百分比。相反，我们使用均方根误差 (RMSE)来衡量模型的“准确性”。
RMSE 的公式为：
电阻米秒乙=∑一世 = 一世n(吨一世-米○d电子升(吨电子秒吨一世))2n
在哪里 吨一世 是测试数据集的实际测试目标特征值和 米○d电子升(吨电子秒吨一世) 是我们训练的回归树模型为这些预测的值 吨一世. 一般来说，RMSE 值越低，我们的模型就越适合实际数据。
由于我们现在已经调整了我们的主要 ID3分类树算法来处理连续缩放的目标特征，并因此将其转化为回归树模型，因此我们可以开始在 Python 中实现这些更改。
因此我们简单地采用了上一章的分类树模型，并实现了上面提到的两个变化。
Python 中从零开始的回归决策树
正如为实现回归树模型而宣布的，我们将使用 UCI 共享单车数据集，其中我们将使用所有 731 个实例以及原始 16 个属性的子集。作为属性，我们使用以下特征：{'season', 'holiday', 'weekday', 'workingday', 'wheathersit', 'cnt'} 其中 {'cnt'} 特征作为我们的目标特征并代表每天租用的自行车总数。
数据集的前五行如下所示：
将 熊猫 导入为 pd
数据集 = pd 。read_csv ( "data/day.csv" , usecols = [ 'season' , 'holiday' , 'weekday' , 'workingday' , 'weathersit' , 'cnt' ])
数据集。样本（分数= 1 ）。头()
我们现在将开始调整最初创建的分类算法。对于代码的进一步评论，我建议读者阅读上一章关于分类树的内容。
"""
导入所需的 python 包
"""
import pandas as pd
import numpy as np
from pprint import pprint
import matplotlib.pyplot as plt
from matplotlib import style
style 。使用（“五三十八” ）
#导入数据集并定义特征和目标列#
dataset = pd . read_csv ( "data/day.csv" , usecols = [ 'season' , 'holiday' , 'weekday' , 'workingday' , 'weathersit' , 'cnt' ]) 。样本（分数= 1 ）
mean_data = np 。均值(数据集. iloc [:, - 1 ])
############################################### ############################################### #######
########################################### ############################################### ##############
"""
计算
数据集的方差此函数采用三个参数
。1. data = 应为其特征计算方差的数据集
2. split_attribute_name = 应为其计算加权方差的特征的名称
3. target_name =目标特征的名称。此示例的默认值是 "cnt"
"""
def var ( data , split_attribute_name , target_name = "cnt" ):
特征值 = np 。unique ( data [ split_attribute_name ])
feature_variance = 0
for value in feature_values :
#创建数据子集-->沿着split_attribute_name特征的值拆分原始数据
#并重置索引以在使用df时不会遇到错误。 loc[] 操作低于
subset = data 。查询( ' {0} == {1} ' .格式( split_attribute_name , value )) 。reset_index ()
#计算每个子集的加权方差
value_var = ( len ( subset ) / len ( data )) * np . var ( subset [ target_name ], ddof = 1 )
#计算特征的加权方差
feature_variance += value_var
return feature_variance
############################################### ############################################### #######
########################################### ############################################### ##############
def Classification ( data , originaldata , features , min_instances , target_attribute_name , parent_node_class = None ):
"""
分类算法：该函数采用与原始分类算法相同的 5 个参数在
上一章中加上一个参数（min_instances），它定义了最小实例的数量
每个节点作为提前停止标准。
""" #定义
停止条件 --> 如果满足其中之一，我们要返回一个叶子节点#
########这个标准是新的########################
如果所有target_values的值相同，则返回平均值对于此数据集的对象地物的
如果 len个（数据） <= INT （min_instances ）：
返回 NP 。意思是（数据[ target_attribute_name ]）
####################################### #############
#如果数据集为空，则返回原始数据集中的平均目标特征值
elif len ( data ) == 0 :
return np . 均值(原始数据[ target_attribute_name ])
#如果特征空间为空，则返回直接父节点的平均目标特征值 --> 注意#
直接父节点是调用当前算法运行的节点，因此#
平均目标特征值为存储在 parent_node_class 变量中。
elif len ( features ) == 0 ：
返回 parent_node_class
#如果以上都不成立，那就种树吧！
else :
#设置此节点的默认值 --> 当前节点的平均目标特征值
parent_node_class = np . mean ( data [ target_attribute_name ])
#选择最能分割数据集的特征
item_values = [ var ( data , feature ) for feature in features ] #返回数据集中特征的方差
best_feature_index = np . argmin （item_values ）
best_feature = 特征[ best_feature_index ]
#创建树结构。根获取具有最小方差的特征（best_feature）的名称。
树 = { best_feature :{}}
#从特征空间中移除方差最小的特征
features = [ i for i in features if i != best_feature ]
#为根节点特征的每个可能值在根节点下生长一个分支
对于 价值 的 NP 。unique ( data [ best_feature ]):
value = value
#按照方差最小的特征
值拆分数据集，从而创建 sub_datasets sub_data = data 。其中（数据[ best_feature ] == 值）。滴滴()
#使用新参数为每个子数据集调用分类算法 --> 递归来了！
subtree = 分类（sub_data ，originaldata ，features ，min_instances ，'cnt' ，parent_node_class = parent_node_class ）
#添加子树，从sub_dataset生长到根节点
树下的树[ best_feature ][ value ] = subtree
返回 树
############################################### ############################################### #######
########################################### ############################################### ##############
"""
预测查询实例
"""
高清 预测（查询，树，默认 = mean_data ）：
为 关键 的 列表（查询。键（））：
如果 键 在 列表（树。键（））：
尝试：
结果 = 树[关键] [查询[关键]
除了：
返回 默认
结果 = 树[键][查询[key ]]
if isinstance ( result , dict ):
return predict ( query , result )
else :
return result
############################################### ############################################### #######
########################################### ############################################### ##############
"""
创建训练集和测试集
"""
def train_test_split ( dataset ):
training_data = dataset . iloc [: int ( 0.7 * len ( dataset ))] 。reset_index ( drop = True ) #我们删除索引分别重新标记索引
#starting form 0，因为我们不想遇到关于行标签/索引
testing_data = dataset 的错误。iloc [ int ( 0.7 *len (数据集)):] 。reset_index （降=真）
返回 training_data ，testing_data
training_data = train_test_split （数据集）[ 0 ]
testing_data = train_test_split （数据集）[ 1 ]
############################################### ############################################### #######
########################################### ############################################### ##############
"""
Compute the RMSE
"""
def test ( data , tree ):
#Create new query instances通过简单地从原始数据集中删除目标特征列并将其
#convert 到字典
queries = data 。iloc [:,: - 1 ] 。to_dict ( orient = "records" )
＃创建在其列树的预测被存储在数据帧空
预测 = []
#Calculate的RMSE
为 我 在 范围（len个（数据））：
预测。追加（预测（查询[ i ]，树，mean_data ））
RMSE = np 。sqrt ( np . sum ((( data . iloc [:, - 1 ] -预测)** 2 ) / len (数据)))
返回 RMSE
############################################### ############################################### #######
########################################### ############################################### ##############
"""
训练树，打印树并预测准确率
"""
tree = Classification ( training_data , training_data , training_data . columns [: - 1 ], 5 , 'cnt' )
pprint ( tree )
print ( '#' * 50 ）
打印（'均方根误差（RMSE）：' ，测试（testing_data ，树））
输出：
{'季节'：{1：{'天气'：{1.0：{'工作日'：{0.0：{'假期'：{0.0：{'工作日'：{0.0：2398.1071428571427，
6.0：2398.1071428571427}}，
1.0: 2540.0}},
1.0：{'假期'：{0.0：{'工作日'：{1.0：3284.28，
2.0: 3284.28,
3.0: 3284.28,
4.0：3284.28，
5.0：3284.28}}}}}}，
2.0：{'假期'：{0.0：{'工作日'：{0.0：2586.8，
1.0：2183.6666666666665，
2.0：{'工作日'：{1.0：2140.6666666666665}}，
3.0：{'工作日'：{1.0：2049.0}}，
4.0：{'工作日'：{1.0：3105.714285714286}}，
5.0：{'工作日'：{1.0：2844.5454545454545}}，
6.0：{'工作日'：{0.0：1757.1111111111111}}}}，
1.0: 1040.0}},
3.0：473.5}}，
2: {'weathersit': {1.0: {'workingday': {0.0: {'weekday': {0.0: {'holiday': {0.0: 5728.2}},
1.0：5503.666666666667，
5.0: 3126.0,
6.0：{'假期'：{0.0：6206.142857142857}}}}，
1.0：{'假期'：{0.0：{'工作日'：{1.0：5340.06，
2.0：5340.06，
3.0：5340.06，
4.0：5340.06，
5.0：5340.06}}}}}}，
2.0：{'假期'：{0.0：{'工作日'：{0.0：{'工作日'：{0.0：4737.0，
6.0：4349.7692307692305}}，
1.0：{'工作日'：{1.0：4446.294117647059，
2.0：4446.294117647059，
3.0：4446.294117647059，
4.0：4446.294117647059，
5.0：5975.333333333333}}}}}}，
3.0：1169.0}}，
3: {'weathersit': {1.0: {'holiday': {0.0: {'workingday': {0.0: {'weekday': {0.0: 5715.0,
6.0：5715.0}}，
1.0：{'工作日'：{1.0：6148.342857142857，
2.0：6148.342857142857，
3.0：6148.342857142857，
4.0：6148.342857142857，
5.0：6148.342857142857}}}}，
1.0：7403.0}}，
2.0：{'工作日'：{0.0：{'假期'：{0.0：{'工作日'：{0.0：4537.5，
6.0: 5028.8}},
1.0: 4697.0}},
1.0：{'假期'：{0.0：{'工作日'：{1.0：6745.25，
2.0：5222.4，
3.0：5554.0，
4.0: 4580.0,
5.0：5389.409090909091}}}}}}，
3.0：2276.0}}，
4: {'weathersit': {1.0: {'holiday': {0.0: {'workingday': {0.0: {'weekday': {0.0: 4974.772727272727,
6.0：4974.772727272727}}，
1.0：{'工作日'：{1.0：5174.906976744186，
2.0：5174.906976744186，
3.0：5174.906976744186，
4.0：5174.906976744186，
5.0：5174.906976744186}}}}，
1.0: 3101.25}},
2.0：{'工作日'：{0.0：3795.6666666666665，
1.0: 4536.0,
2.0：{'假期'：{0.0：{'工作日'：{1.0：4440.875}}}}，
3.0：5446.4，
4.0：5888.4，
5.0：5773.6，
6.0：4215.8}}，
3.0：{'工作日'：{1.0：1393.5，
2.0：2946.6666666666665，
3.0：1840.5，
6.0：627.0}}}}}}
###############################################
均方根误差 (RMSE)：1623.9891244058906
上面我们可以看到每个节点最少有 5 个实例的 RMSE。但就目前而言，我们不知道这有多糟糕或有多好。为了了解我们模型的“准确性”，我们可以绘制一种学习曲线，在该曲线中我们根据 RMSE 绘制最小实例的数量。
"""
绘制相对于最小实例数的 RMSE
"""
fig = plt 。图()
ax0 = 图. add_subplot ( 111 )
RMSE_test = []
RMSE_train = []
for i in range ( 1 , 100 ):
tree = Classification ( training_data , training_data , training_data . columns [: - 1 ], i , 'cnt' )
RMSE_test 。追加（测试（测试数据，树））
RMSE_train 。追加（测试（training_data ,树))
轴0 。plot ( range ( 1 , 100 ), RMSE_test , label = 'Test_Data' )
ax0 。plot ( range ( 1 , 100 ), RMSE_train , label = 'Train_Data' )
ax0 。图例()
ax0 。set_title ( 'RMSE 相对于每个节点的最小实例数' )
ax0 。set_xlabel ( '#Instances' )
ax0. set_ylabel ( 'RMSE' )
plt 。显示()
正如我们所见，增加每个节点的最小实例数会导致测试数据的 RMSE 降低，直到我们达到每个节点大约 50 个实例的数量。在这里，Test_Data曲线趋于平缓，并且每片叶子的最小实例数的额外增加不会显着降低我们测试集的 RMSE。
让我们绘制最小实例数为 50 的树。
树 = 分类( training_data , training_data , training_data . columns [: - 1 ], 50 , 'cnt' )
pprint ( tree )
输出：
{'季节'：{1：{'weathersit'：{1.0：{'工作日'：{0.0：2407.56666666666666，
1.0：3284.28}}，
2.0：2331.74，
3.0：473.5}}，
2：{'weathersit'：{1.0：{'工作日'：{0.0：5850.178571428572，
1.0：5340.06}}，
2.0：4419.595744680851，
3.0：1169.0}}，
3: {'weathersit': {1.0: {'holiday': {0.0: {'workingday': {0.0: 5715.0,
1.0：{'工作日'：{1.0：5996.090909090909，
2.0：6093.058823529412，
3.0：6043.6，
4.0：6538.428571428572，
5.0：6050.2307692307695}}}}，
1.0：7403.0}}，
2.0：5242.617647058823，
3.0：2276.0}}，
4: {'weathersit': {1.0: {'holiday': {0.0: {'workingday': {0.0: 4974.772727272727,
1.0：5174.906976744186}}，
1.0: 3101.25}},
2.0：4894.861111111111，
3.0：1961.6}}}}
这就是我们最终的回归树模型。恭喜 - 完成！
sklearn 中的回归树
由于我们现在已经从头开始构建回归树模型，因此我们将使用 sklearn 的预先打包的回归树模型sklearn.tree.DecisionTreeRegressor。该过程遵循通用 sklearn API，并且一如既往：
- 导入模型
- 参数化模型
- 预处理数据并创建描述性特征集以及目标特征集
- 训练模型
- 预测新的查询实例
为方便起见，我们将使用上面的训练和测试数据。
#
从 sklearn.tree 导入 回归树模型import DecisionTreeRegressor
#参数化模型#
我们将使用均值误差==方差作为分割标准并设置
每片叶子
的最小实例数=5回归模型 = DecisionTreeRegressor （标准= “mse” ，min_samples_leaf = 5 ）
#拟合模型
regression_model 。配合（training_data 。ILOC [：，：- 1 ]，training_data 。ILOC [：，- 1 ：]）
#Predict看不见查询实例
预测 = regression_model 。预测（testing_data 。ILOC [：，：- 1 ]）
#计算并绘制RMSE
均方根误差 = np 。SQRT （NP 。总和（（（testing_data 。ILOC [：，- 1 ] -预测的）** 2 ）/ LEN （testing_data 。ILOC [：，- 1 ]）））
RMSE
输出：
1592.7501629176463
每个叶节点参数化的最小数量为 5 个实例，我们得到的 RMSE 与上面我们自己构建的模型几乎相同。同样对于这个模型，我们将针对每个叶节点的最小实例数绘制 RMSE，以评估产生最小 RMSE 的最小实例数参数。
"""
绘制相对于最小实例数的 RMSE
"""
fig = plt 。图()
ax0 = 图. add_subplot ( 111 )
RMSE_train = []
RMSE_test = []
for i in range ( 1 , 100 ):
#Paramterize the model and let i be the number of minimum instances per
Leaf node Regression_model = DecisionTreeRegressor ( criteria = "mse" , min_samples_leaf = i )
#训练模型
regression_model 。配合（training_data 。ILOC [：，：- 1 ]，training_data 。ILOC [：，- 1 ：]）
#Predict查询实例
预测训练 = 回归模型。预测( training_data . iloc [:,: - 1 ])
预测测试 = 回归模型。预测（testing_data 。ILOC [：，：- 1 ]）
#Calculate和追加RMSEs
RMSE_train 。追加（NP 。SQRT （NP 。总和（（（training_data 。ILOC [：，- 1 ] -predicted_train ）** 2 ）/ len个（training_data 。ILOC [：，- 1 ]））））
RMSE_test 。追加（NP 。SQRT （NP 。总和（（（testing_data 。ILOC [：，- 1 ] - predicted_test ）** 2 ）/ LEN （testing_data 。ILOC [：，- 1 ]））））
轴0 。plot ( range ( 1 , 100 ), RMSE_test , label = 'Test_Data' )
ax0 。plot ( range ( 1 , 100 ), RMSE_train , label = 'Train_Data' )
ax0 。图例()
ax0 。set_title ( 'RMSE 相对于每个节点的最小实例数' )
ax0 。set_xlabel ( '#Instances' )
ax0. set_ylabel ( 'RMSE' )
plt 。显示()
使用 sklearns 预先打包的回归树模型产生最小的 RMSE ≈每个节点 10 个实例。但是，相对于实例数的最小 RMSE 值是≈与使用我们自己创建的模型计算的相同。此外，sklearns 决策树模型的 RMSE 也会因每个节点的大量实例而变平。
扫一扫
2858
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
