搜索策略

搜索策略

搜索是由初始状态到目标状态的求解过程，就搜索结果分类，分为可行解搜索1和最优解搜索2。搜索策略是在求解过程中使用的方法。搜索往往是通过树的形式来描述。

搜索方式

广度优先搜索(BFS)

1. 构造由根组成的队列Q
2. If Q 的第一个元素x是目标节点 Then 停止
3. 从Q 中删除x，把x的所有子节点加入Q的末尾
4. If Q空 Then 失败 Else goto 2

深度优先搜索(DFS)

1. 构造一个由根构成的单元素栈S
2. If Top(S) 是目标节点 Then 停止
3. Pop(S)，把Top(S)的所有子节点压入栈
4. If S空 Then 失败 Else goto 2

单纯的BFS、DFS都是属于盲搜的，这时候就需要结合一些优化手段起到指引作用，从而加速搜索速度。

搜索的优化策略

爬山策略

在深度优先搜索(DFS)的过程中，经常遇到多个节点可以扩展的情况，但是首先应该扩展哪个节点呢？

爬山策略使用贪心法确定搜索的方向，是优化的深度优先遍历搜素策略。

爬山策略使用启发式测度来排序节点扩展的顺序。

1. 构造由根组成的单元素栈S
2. If Top(S) 是目标节点 Then 停止
3. Pop(S)
4. S的子节点按照其启发测度由大到小的顺序压入S
5. If S空 Then 失败 Else goto 2.

测度算法

启发式测度算法举例：八数码——路径寻找问题
在八数码问题中，就是要找到从初始状态到目标状态的一条可行路径。

启发式测度算法$f(n)$可以设计为以某一状态不在目标状态的位置个数作为测度。

比如目标位置为： $\begin{bmatrix} 1 & 2 & 3 \\ 8 & & 4 \\ 7 & 6 & 5 \end{bmatrix}$，当前状态为： $\begin{bmatrix} 2 & & 3 \\ 1 & 8 & 4 \\ 7 & 6 & 5 \end{bmatrix}$，则$f(i) = 3$。

Best-First搜索策略

结合深度优先和广度优先的优点。

根据一个评价函数，在目前产生的所有节点中选取具有最小评价函数值的节点进行扩展。

具有全局优化观念，而爬山法仅有局部优化观念。

1. 使用评价函数构造一个堆H，首先构造由根组成的单元素堆
2. If H 的根r是目标节点 Then 停止
3. 从H中删除r，把r的子节点插入H
4. If H空 Then 失败 Else goto 2

评价算法

评价算法可以参考测度算法

分支限界

基本思想

上述方法很难用于求解优化问题

分支限界策略可以有效地求解组合优化问题

发现优化解的一个界限

缩小解空间，提高求解的效率

原理

• 产生分支的机制(使用前面的任意一种策略)
• 产生一个界限(可以通过发现可能解)
• 进行分支限界搜索
• 分支限界搜素以广度优先或以最小耗费(最大收益)优先的方式搜索解空间，并在搜索过程中用剪枝函数避免无效搜索。

常见的两种分支限界的算法框架

1. 队列式(FIFO)分支限界法：按照队列先进先出(FIFO)的原则选取下一个节点为扩展节点。
2. 优先队列式分支限界法：按照优先队列中规定的优先级选取优先级最高的节点成为当前扩展节点。

举例：多阶段图搜索问题

求从$V_0$到$V_3$的最短路径

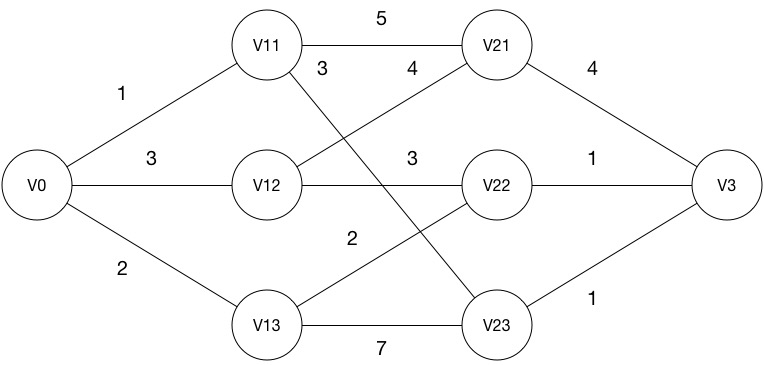
多阶段图

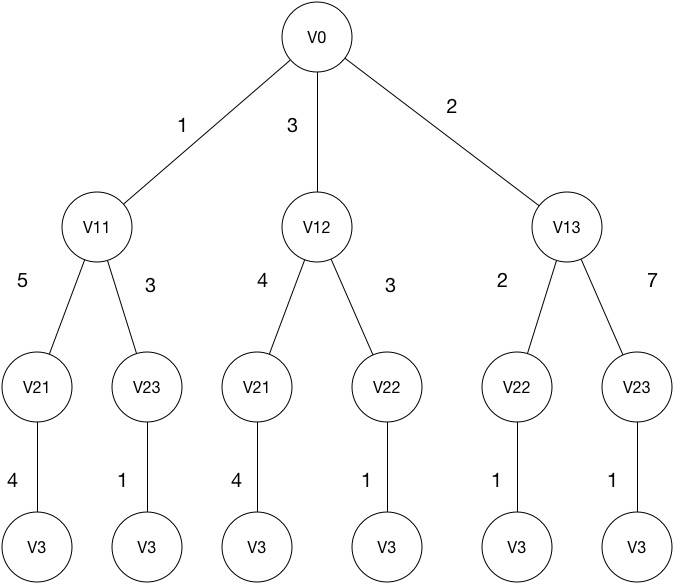
问题的树表示

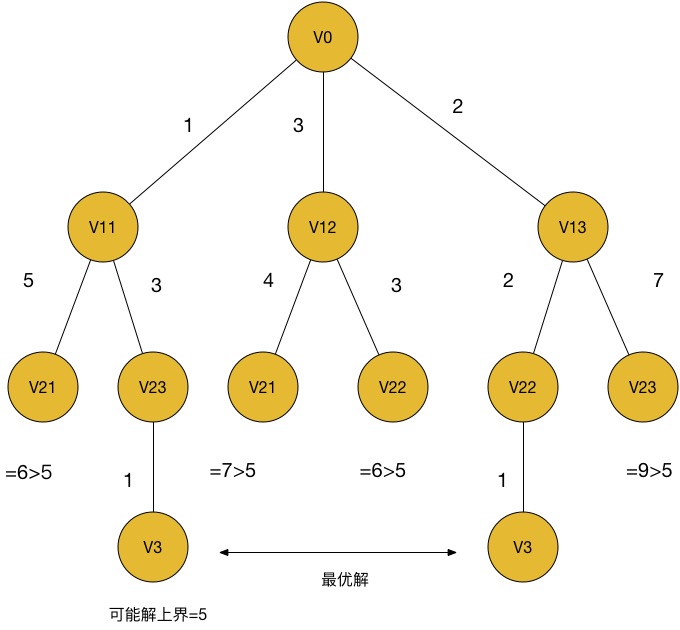
使用爬山策略进行分支限界搜索

---

1. 可行解搜索的目的是找到解空间里面的一个可行解。 ↩
2. 最优解搜索的目的是找到解空间里面的最优解，在没有一定策略的情况下是需要搜索整个解空间的，其时间复杂度就是指数时间的了。 ↩