博客:http://blog.csdn.net/qianxin_dh
邮箱:qianxin_dh@163.com
目前在目标检测任务中,由于svm自身具有较好的推广能力以及对分类的鲁棒性,得到了越来越多的应用。 Struck算法便使用了在线结构输出svm学习方法去解决跟踪问题。不同于常规算法训练一个分类器,Struck算法直接通过预测函数: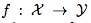 ,来预测每帧之间目标位置发生的变化,其中
,来预测每帧之间目标位置发生的变化,其中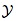 表示搜寻空间,例如,
表示搜寻空间,例如,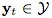 ,上一帧中目标的新位置为Pt-1,则在当前帧中,目标位置就为
,上一帧中目标的新位置为Pt-1,则在当前帧中,目标位置就为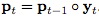 (可见
(可见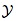 其实就是表示帧间目标位置变化关系的集合)。因此,在Struck算法中,已知类型的样本用(x,y)表示,而不再是(x,+1)或者(x,-1)了。
其实就是表示帧间目标位置变化关系的集合)。因此,在Struck算法中,已知类型的样本用(x,y)表示,而不再是(x,+1)或者(x,-1)了。
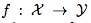 ,来预测每帧之间目标位置发生的变化,其中
,来预测每帧之间目标位置发生的变化,其中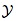 表示搜寻空间,例如,
表示搜寻空间,例如,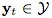 ,上一帧中目标的新位置为Pt-1,则在当前帧中,目标位置就为
,上一帧中目标的新位置为Pt-1,则在当前帧中,目标位置就为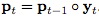 (可见
(可见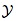 其实就是表示帧间目标位置变化关系的集合)。因此,在Struck算法中,已知类型的样本用(x,y)表示,而不再是(x,+1)或者(x,-1)了。
其实就是表示帧间目标位置变化关系的集合)。因此,在Struck算法中,已知类型的样本用(x,y)表示,而不再是(x,+1)或者(x,-1)了。
那么y预测函数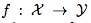 怎么获得呢?这就需要用到结构输出svm方法了(svm基本概念学习可参考我上篇文章中给出的svm三重境界的链接),它在该算法中引入了一个判别函数
怎么获得呢?这就需要用到结构输出svm方法了(svm基本概念学习可参考我上篇文章中给出的svm三重境界的链接),它在该算法中引入了一个判别函数![]()
![]()
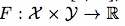 ,通过公式
,通过公式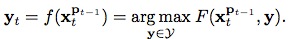 找到概率最大的
找到概率最大的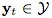 对目标位置进行预测,也就是说,因为我们还不知道当前帧的目标位置,那么我们首先想到在上一帧中的目标能够通过一些位置变化关系,出现在当前帧中的各处,但是呢,实际的目标只有一个,所以这些变换关系中也必然只有一个是最佳的,因此,我们需要找到这个最佳的,并通过
对目标位置进行预测,也就是说,因为我们还不知道当前帧的目标位置,那么我们首先想到在上一帧中的目标能够通过一些位置变化关系,出现在当前帧中的各处,但是呢,实际的目标只有一个,所以这些变换关系中也必然只有一个是最佳的,因此,我们需要找到这个最佳的,并通过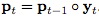 ,就可以成功找到目标啦~,至于搜寻空间
,就可以成功找到目标啦~,至于搜寻空间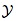 如何取,在程序解读时大家就会看到了。
如何取,在程序解读时大家就会看到了。
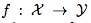 怎么获得呢?这就需要用到结构输出svm方法了(svm基本概念学习可参考我上篇文章中给出的svm三重境界的链接),它在该算法中引入了一个判别函数
怎么获得呢?这就需要用到结构输出svm方法了(svm基本概念学习可参考我上篇文章中给出的svm三重境界的链接),它在该算法中引入了一个判别函数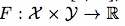 ,通过公式
,通过公式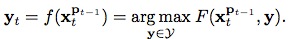 找到概率最大的
找到概率最大的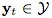 对目标位置进行预测,也就是说,因为我们还不知道当前帧的目标位置,那么我们首先想到在上一帧中的目标能够通过一些位置变化关系,出现在当前帧中的各处,但是呢,实际的目标只有一个,所以这些变换关系中也必然只有一个是最佳的,因此,我们需要找到这个最佳的,并通过
对目标位置进行预测,也就是说,因为我们还不知道当前帧的目标位置,那么我们首先想到在上一帧中的目标能够通过一些位置变化关系,出现在当前帧中的各处,但是呢,实际的目标只有一个,所以这些变换关系中也必然只有一个是最佳的,因此,我们需要找到这个最佳的,并通过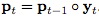 ,就可以成功找到目标啦~,至于搜寻空间
,就可以成功找到目标啦~,至于搜寻空间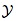 如何取,在程序解读时大家就会看到了。
如何取,在程序解读时大家就会看到了。
那么如何找到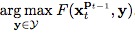 呢?我个人理解是:将判别函数形式转换为:
呢?我个人理解是:将判别函数形式转换为: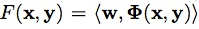 ,其中,
,其中,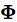 表示映射函数,是从输入空间到某个特征空间的映射,进而实现对样本线性可分。因为当分类平面(输入空间中的超平面)离数据点的“间隔”越大,分类的确信度越大,所以需让所选择的分类平面最大化这个“间隔”值,这里我们通过最小化凸目标函数
表示映射函数,是从输入空间到某个特征空间的映射,进而实现对样本线性可分。因为当分类平面(输入空间中的超平面)离数据点的“间隔”越大,分类的确信度越大,所以需让所选择的分类平面最大化这个“间隔”值,这里我们通过最小化凸目标函数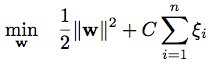 来实现,该函数应满足条件:
来实现,该函数应满足条件: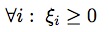 和
和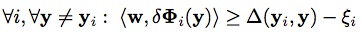 ,其中,
,其中, ,
,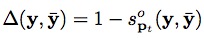 (
(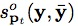 表示两个框之间的覆盖率)。优化的目的是确保F(目标)>>F(非目标)。
表示两个框之间的覆盖率)。优化的目的是确保F(目标)>>F(非目标)。
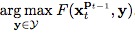 呢?我个人理解是:将判别函数形式转换为:
呢?我个人理解是:将判别函数形式转换为: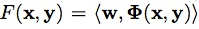 ,其中,
,其中,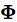 表示映射函数,是从输入空间到某个特征空间的映射,进而实现对样本线性可分。因为当分类平面(输入空间中的超平面)离数据点的“间隔”越大,分类的确信度越大,所以需让所选择的分类平面最大化这个“间隔”值,这里我们通过最小化凸目标函数
表示映射函数,是从输入空间到某个特征空间的映射,进而实现对样本线性可分。因为当分类平面(输入空间中的超平面)离数据点的“间隔”越大,分类的确信度越大,所以需让所选择的分类平面最大化这个“间隔”值,这里我们通过最小化凸目标函数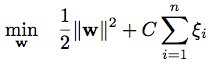 来实现,该函数应满足条件:
来实现,该函数应满足条件: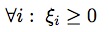 和
和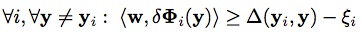 ,其中,
,其中, ,
,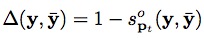 (
(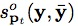 表示两个框之间的覆盖率)。优化的目的是确保F(目标)>>F(非目标)。
表示两个框之间的覆盖率)。优化的目的是确保F(目标)>>F(非目标)。
接下来问题又来了,如何获得最小的w??文中采取的求解方式是利用拉格朗日对偶性,通过求解与原问题等价的对偶问题(dual problem),得到原始问题的最优解。通过给每一个约束条件加上一个拉格朗日乘子alpha,定义拉格朗日函数L(w,b,alpha)。一般对偶问题的求解过程如下:1)固定alpha,求L关于w,b的最小化。2)求L对alpha的极大。3)利用SMO算法求得拉格朗日乘子alpha。为了简化对偶问题求解,这里定义了参数beta,可见论文中的Eq.(8)。
算法主要流程:








 该博客介绍了Struck目标跟踪算法的初始化和更新过程,包括Config类的配置读取、图像尺寸统一、以及Initiale、UpdateLearner、Update等关键步骤。通过Debug()函数显示跟踪效果,用绿色和红色边框区分正负样本。
该博客介绍了Struck目标跟踪算法的初始化和更新过程,包括Config类的配置读取、图像尺寸统一、以及Initiale、UpdateLearner、Update等关键步骤。通过Debug()函数显示跟踪效果,用绿色和红色边框区分正负样本。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 6697
6697

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








