最近在看Andrew Ng的机器学习课程,将学到的东西在此做个总结,加深印象。顺便结合Weka将部分算法在上面实现,讲解部分自己调参数的心得体会,让大家少走弯路。
这篇博客主要涉及到前4个视频,和第一个讲义,主要内容是关于判别学习方法的,涉及到了梯度下降、随机梯度下降、最小二乘法、局部加权回归、极大似然原理、logistic regression、牛顿方法、广义线性模型、指数分布族。下面就主要内容尝试进行总结,由于我也并非大牛,有错误地方希望指正。也欢迎与我交流,一起进步和学习。
- 问题引入:房价预测
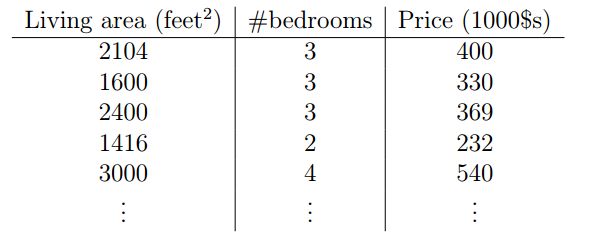
首先是引入回归问题,用了一个房屋售卖的例子,数据如下图:
我们可以将变量表示成X1,X2,然后结果表示为Y,那么Y和X之间存在一种映射关系,也就是说,我们可以通过X预测Y,假设二者之间关系是多元线性关系,形式上表述为:
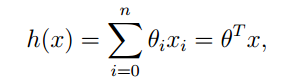
H就是根据X对Y做出的估计,其中的参数θ是我们要求的量。
如何求得参数θ呢?我们可以利用损失函数的概念,损失函数表示了预测值与实际值之间的差距:
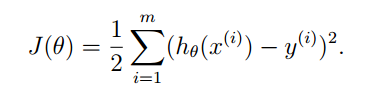
那么很显然,只要J(θ)最小化,那么θ就是最好的参数。那么我们下面就是使得J(θ)最小化,其中方法之一梯度下降方法。
- 梯度下降
什么是梯度?梯度是标量场中某一点上的梯度指向标量场增长最快的方向,梯度的长度是这个最大的变化率。因此,梯度方向是函数变化最快的地方。那么我们可以任意初始化θ,接下来就按照梯度方向进行调整θ只,就可以最快的到达最大值。
可以得到更新θ规则,对于一个独立的样本,这种方法就是最小二乘法。
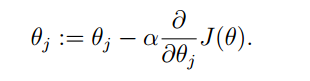
扩展到M个样本,对J(θ)求偏导数,可以得到最终结果:
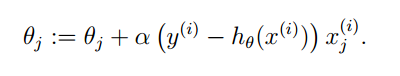
因此,梯度下降的过程就是不断地θ进行迭代,直到θ达到最大值为止
但是这样有一个很大的问题,就是每下降一步,就需要遍历整个数据集,这会导致巨大的计算量。因此,我们可以每次使用一条数据,就迭代一次,过程如下:
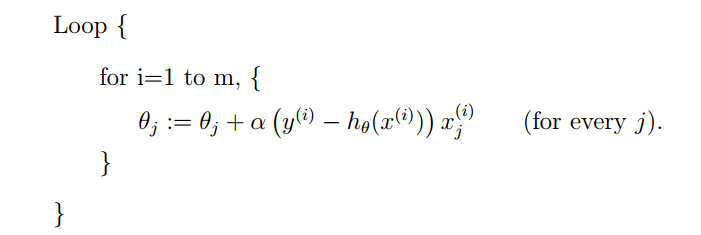
这样就会使得迭代过程并非一直是正向进行的,也就是可能会有向相反方向迭代的可能,但是总体还是向下的。这样还有一个问题,就是可能算法未必会收敛到最小值,而在最小值附近一直徘徊。但是最大的优点就是,快!
除了代数方法求得θ,我们还可以使用线性代数的方法直接求得θ参数,具体推导过程不再赘述,可以去看讲义,结果是:
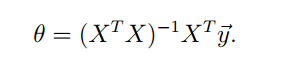
这样虽然避免了计算,但是对矩阵求逆是比较慢的,而且这个方法要求X是满秩的,若不是满秩矩阵需要做处理。
- 极大似然估计
那么为什么采用平方和函数得到的θ就是最佳的呢?这里有对应的概率解释。对于一般的回归问题,我们可以将预测值和真实值之间表示为:
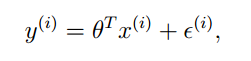
后面一项是误差,那么误差的概率分布是什么呢?
Ng的解释是一般情况下当成正态分布处理,因为按照中心极限定理,很多变量独立同分布时,误差分布趋向于正态分布。
因此误差的概率分布是:
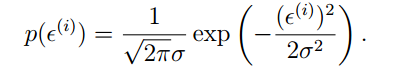
那么可以得到目标值Y的概率分布:
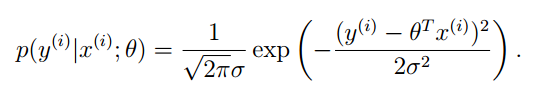
那么可以得到目标值Y的最大似然估计函数:
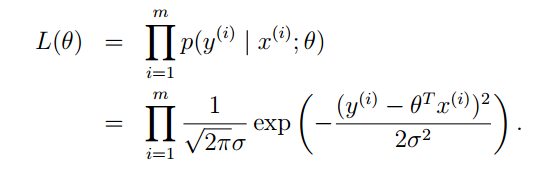
连乘形式不便于计算,我们两边取对数,化简可以得到:
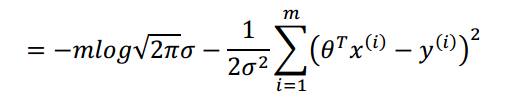
这就是平方和最小问题。也就从数学上证明了平方和最小函数能够解出最佳的θ。
- 局部加权回归
有时候可能我们发现变量X和Y之间的关系并不是一种线性关系,但是在很小一段上,X和Y可以近似的看做线性关系,那么如何衡量这种关系呢?我们可以使用局部加权回归来解决这类问题,通过权重函数,我们可以距离目标值越远的点对整体影响越小。
那么我们的问题可以化为:
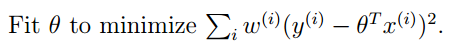
其中,W可以表示为:
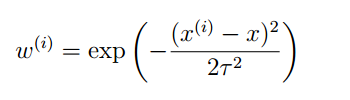
这里面的τ被称为波长,用于控制权值随着距离变化的快慢。
那么我们像之前一样对问题进行求解。
- logistic回归
有时候,我们的预测值并不是连续的,如满足伯努利分布,Y∈{0,1},那么该怎么进行回归分析呢?
我们可以利用函数将连续值映射到0-1之间,一个函数就是:
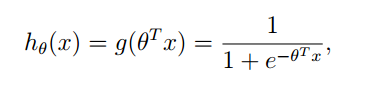
使用该函数可以将连续值映射到0-1之间。
那么我们可以得到Y的概率分布:
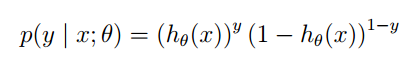
利用最大似然方法,可以求得θ的更新方式:
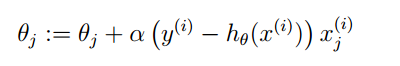
有人发现这个公式和最小二乘法的公式很像,其实二者并没有什么关系,因为Hθ函数完全不同。
事实上,只要是使用梯度下降方法得到的θ更新方法形式上都差不多。
如果我们将所有连续值都映射为0和1两个值,也就是
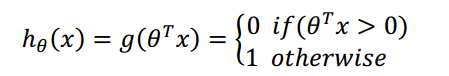
这样求得的θ的算法就是感知器算法。
- 牛顿方法
除了梯度下降,还有一种牛顿方法可以对解空间进行搜索。示意图如下:
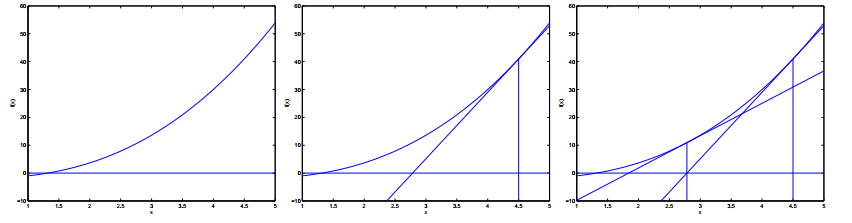
方法是先随机选一个点,求出该点的切线,延长它使之与 x 轴相
交,以相交时的 x 的值作为下一次迭代的值。
由于最大似然函数的性质,我们可以知道当导数为0时,求得θ最佳,那么我们可以得到更新规则:
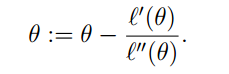
牛顿法的优点是收敛较快,但是有可能达不到最值。
- 指数分布族和广义线性模型
其实对于一般的分布,都可以归结到指数分布族上。也就是它的概率分布可以表示为指数的形式。高斯分布、伯努利分布等分布都可以通过适当的变换转化成指数分布的形式。
那么这些分布既然都可以统一到一种分布上,那么这些分布的数据能不能用一种统一的模型来表示呢?答案是肯定的,这就是GLM,广义线性回归。
使用广义线性回归可以结局很多分布问题,例如多项式分布,假设目标值有K个,{1,2,3,……,k}我们可以将T(y)表示为:
只需要K-1的变量就可以了,因为所有的概率加起来是1.
我们还要再定义指示函数:
T(True)=1,都则为0。
那么我们经过推导,可以得到Hθ(x)的表示:
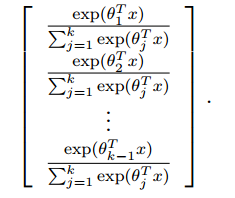
这样我们可以写出最大似然估计的表达式Lθ,然后运用梯度下降进行求解即可。
- 使用Weka实现Logistic 回归
Weka中实现了Logistic回归,实现方法非常简单,和之前一篇博客中提到的J48差不多:

参数比较少,其中-R用来调整迭代时θ对整个Cost函数的影响,默认是1E-8,-M是迭代的最大次数,如果指定为-1,则算法运行一直到收敛为止。
代码如下:
class LogisticModel {
public LogisticModel(Instances data) {
String[] options={"-M",20};
Logistic model = new Logistic();
try {
model.setOptions(options);
model.buildClassifier(data);
} catch (Exception e) {
e.printStackTrace();
}
}
}







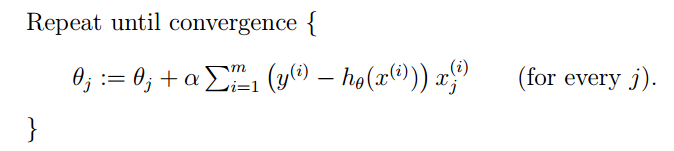
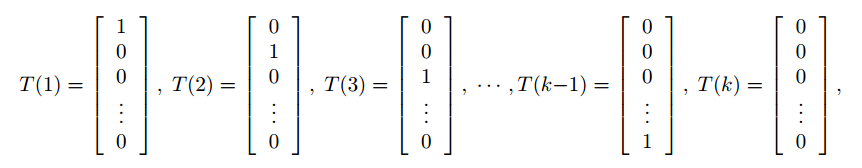
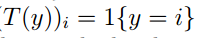














 201
201

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








