小学奥数

小学奥数

24点游戏

现在有一堆牌,从中拿四张牌,用 + , - , * , / 如果凑出24,你就赢了.
从中尽可能多的用乘法,凑出3和8，4和6，2和12.
2 3 8 9
算式：$8÷2\ast (9-3)=24$

抽屉原理

假如有10个苹果，要放进3个抽屉里,先求出每个抽屉里放的,用10/3,因为要求至少有多少个苹果，所以余数要平均分配.
20 6
算式：$20÷6=\mathrm{3......2}$

复杂奇偶性问题

$偶数+-偶数=偶数$
$偶数+-奇数=偶数$
$奇数+-奇数=偶数$
$偶数\ast 偶数=偶数$
$偶数\ast 奇数=偶数$
$奇数\ast 奇数=奇数$
$1\ast 3+3\ast 5+5\ast 7+...+31\ast 33$的结果是____。
A奇数 B偶数 C不能确定
正确答案： B
解答：
每一项乘积都是奇数，共有$32÷2=16$个，16个奇数相加，结果为偶数。

和同近积大

张大爷今年在一个“L”形墙角围了一个长为22米的长方形篱笆，那么该篱笆所圈的面积最大是____平方米。
正确答案：121
解答：
篱笆的长+宽的和为22米，长与宽越接近，乘积越大，因此面积最大为$11\ast 11=121$平方米。

算式最值

将1~6这6个数分别填入算式□□□*□□□的□中，那么算式结果最大是_____
正确答案：342002
解答：
要使乘积最大，6和5放在首尾，1和2放在各位，那这两个数的合为1173，和固定，相差越小积越大，所以最大为$631\ast 542=342002$。

枚举法构造抽屉

这是以前的抽屉问题

这是现在的抽屉原理

现在一共有9种可能，分别是足球、篮球、排球、足球和足球、篮球和篮球、排球和排球、足球和篮球、足球和排球、篮球和排球。在用$20÷9$,等于2有余数，我们就可以说有$2+1=3$个同学，拿到的球的数量和种类完全一样。

但如果现在要求有多少个同学，还得保证一定有4个人拿到的情况一样，就给他捣乱，最倒霉的情况就是每个抽屉都有3个人，现在，只要在拿一个，就一定能保证4个人拿到的情况一样了，最后能求出有$3\ast 9+1$个同学。

排列组合辨析

排列和组合非常像，都是从一些物体中挑出几个来，这两个的区别就是要不要考虑顺序，排列是挑出来还得排一排，要考虑顺序，而组合就是和顺序没有关系，比如：

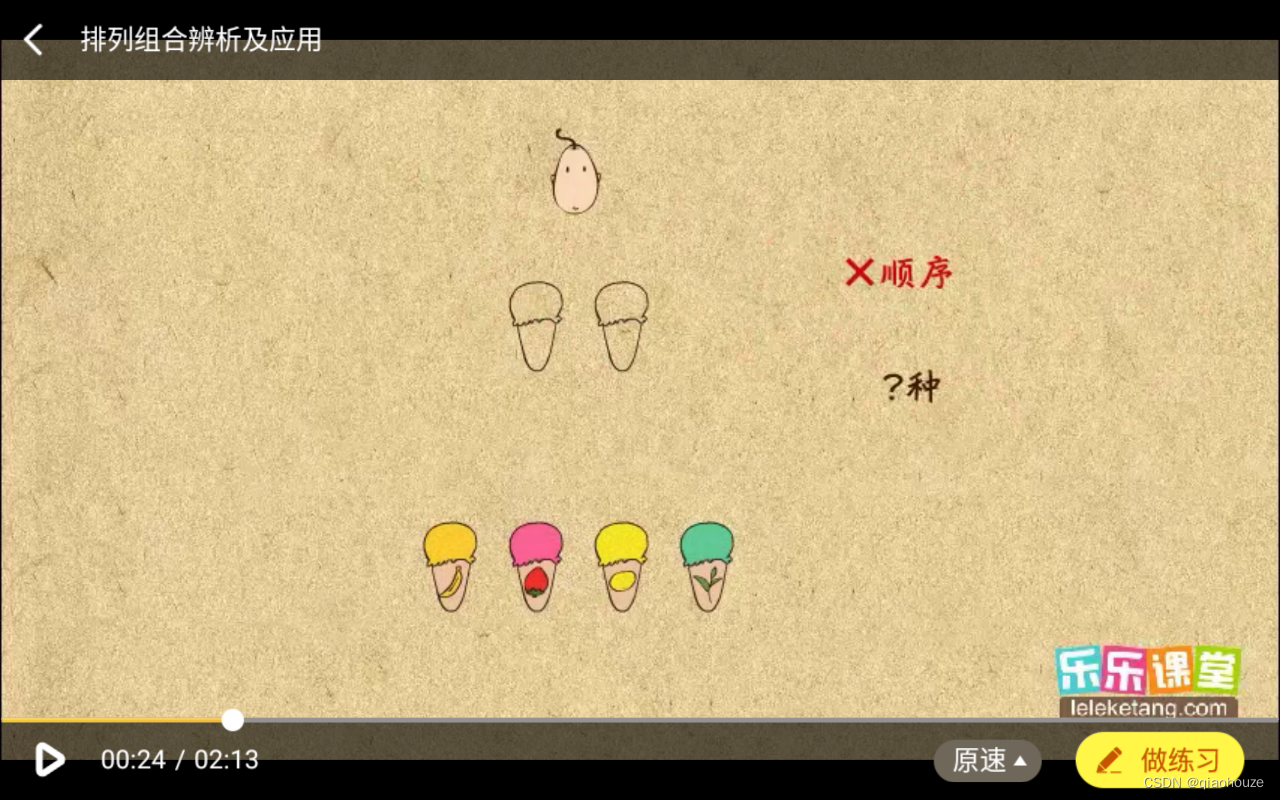
这里不用考虑顺序，可以用组合来求,算式是$C_4^2$(这里$C_4^2$表示在四个里面选两个)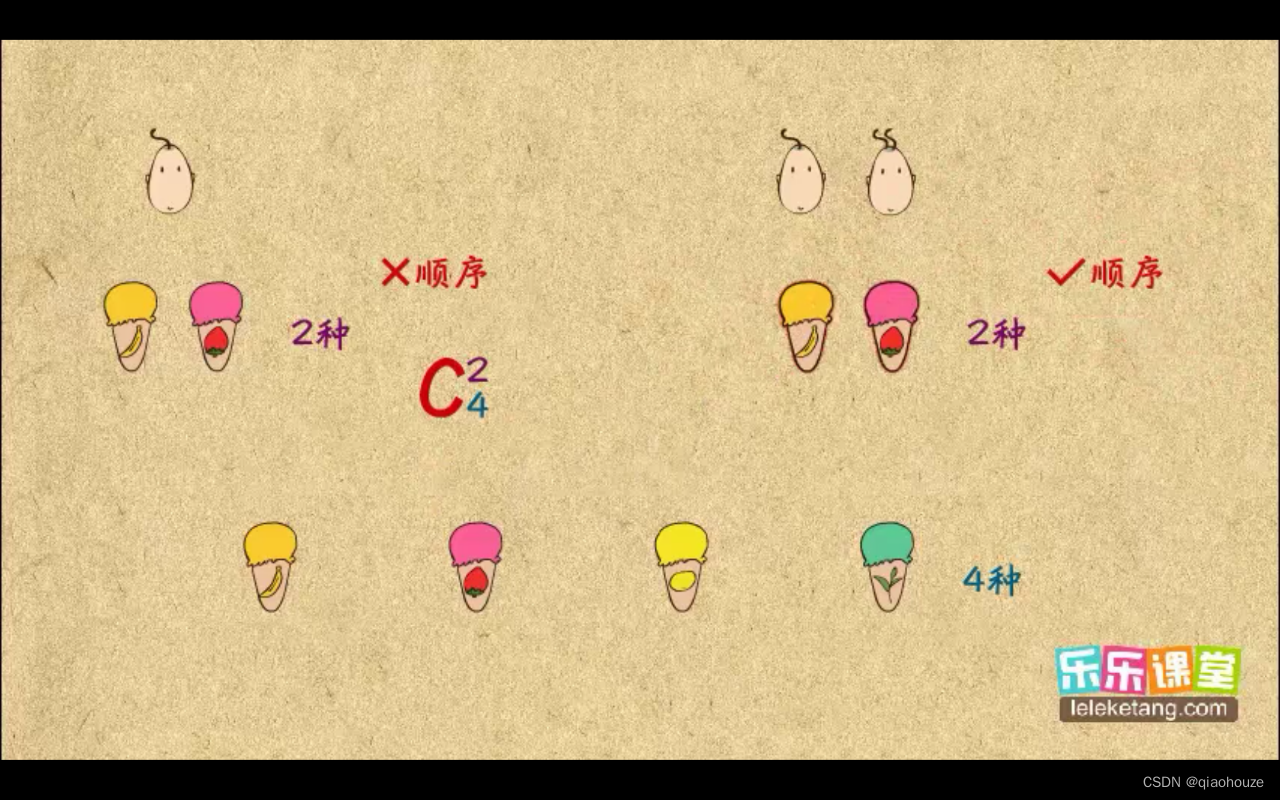
如果给两个人买冰激凌的的话，就得考虑顺序，用排列，算式是$A_4^2$(这里$A_4^2$表示在四个里面选两个,而且考虑顺序)

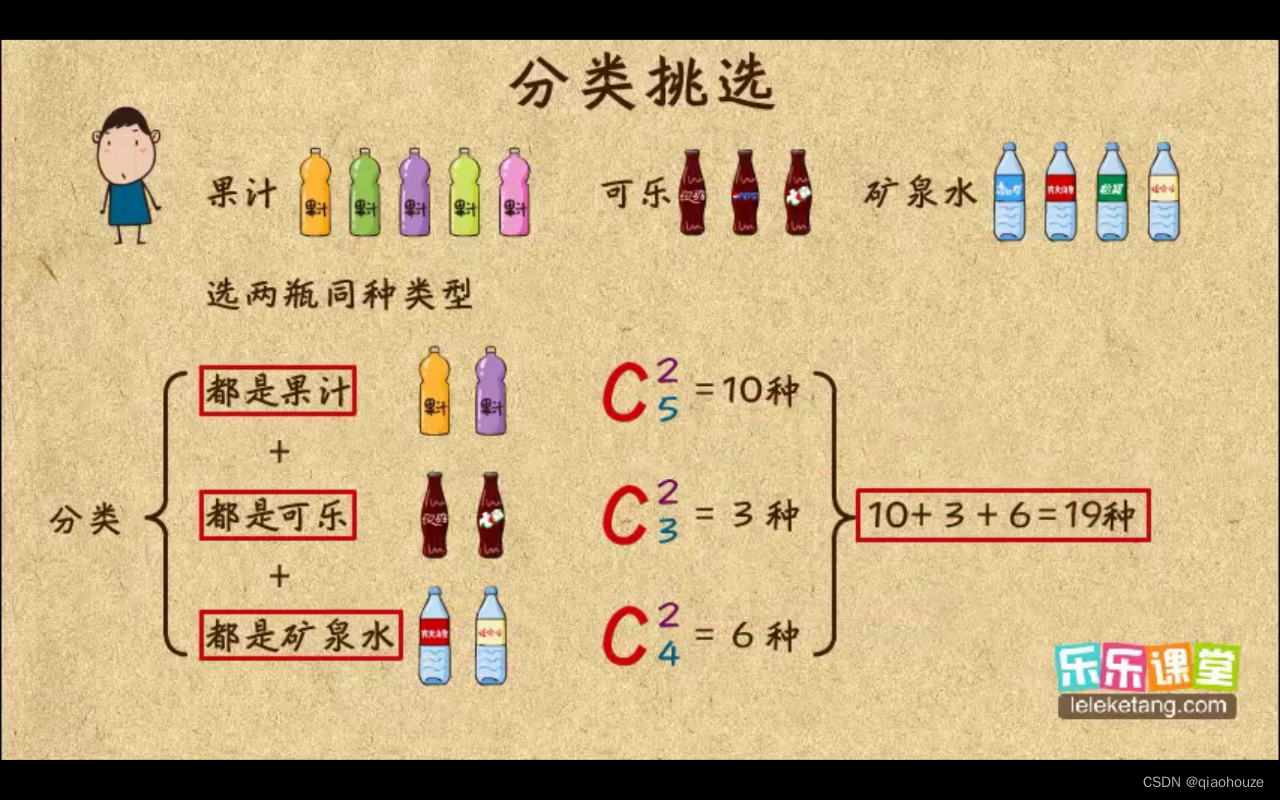
分类挑选

豆豆和牛牛到山上郊游，豆豆要带喝的，有五瓶果汁，三瓶可乐和四瓶不同的矿泉水，要挑选两瓶同种类型，有多少种可能呢？可能都是果汁，可乐或矿泉水，就得分成三类来算，最后把他们加起来，就是答案最后的算式$C_5^2+C_3^2+C_4^2=19$,所以最后有19种方法

现在牛牛也要挑饼干，可以挑6袋饼干和5袋面包，要挑四袋，至少有两袋饼干，那么有多少种可能呢？饼干至少有两袋，可以分成2袋，3袋，4袋，这样来算，算式就是$C_6^2\ast C_5^2+C_6^3\ast C_5^1+C_6^4=150+100+15=265$种,所以有265种。

练习题

有10个三好学生，要把这10个学生分配到7个班里，有几种分法？
解答：
把三个学生分到三个班级
把三个学生分到两个班级
把三个学生分到一个班级
$C_7^3+A_7^2+C_7^1=84$