Counting Bits 计算二进制形式中的1的个数

Given a non negative integer number num. For every numbers i in the range 0 ≤ i ≤ num calculate the number of 1's in their binary representation and return them as an array.

Example:
For num = 5 you should return [0,1,1,2,1,2].

Follow up:

• It is very easy to come up with a solution with run time O(n*sizeof(integer)). But can you do it in linear time O(n) /possibly in a single pass?
• Space complexity should be O(n).
• Can you do it like a boss? Do it without using any builtin function like __builtin_popcount in c++ or in any other language.

Hint:

1. You should make use of what you have produced already.
2. Divide the numbers in ranges like [2-3], [4-7], [8-15] and so on. And try to generate new range from previous.

1. Or does the odd/even status of the number help you in calculating the number of 1s?

首先，我们计算一部分数的二进制中的1的个数看看。

如图，我们可以发现[4-7]的结果是前面[0-3]的值+1

[8-15]的结果是前面[0-7]的值+1

所以，我们得到了如何根据前面已经计算好的值，计算当前值的规律。

运行时间：

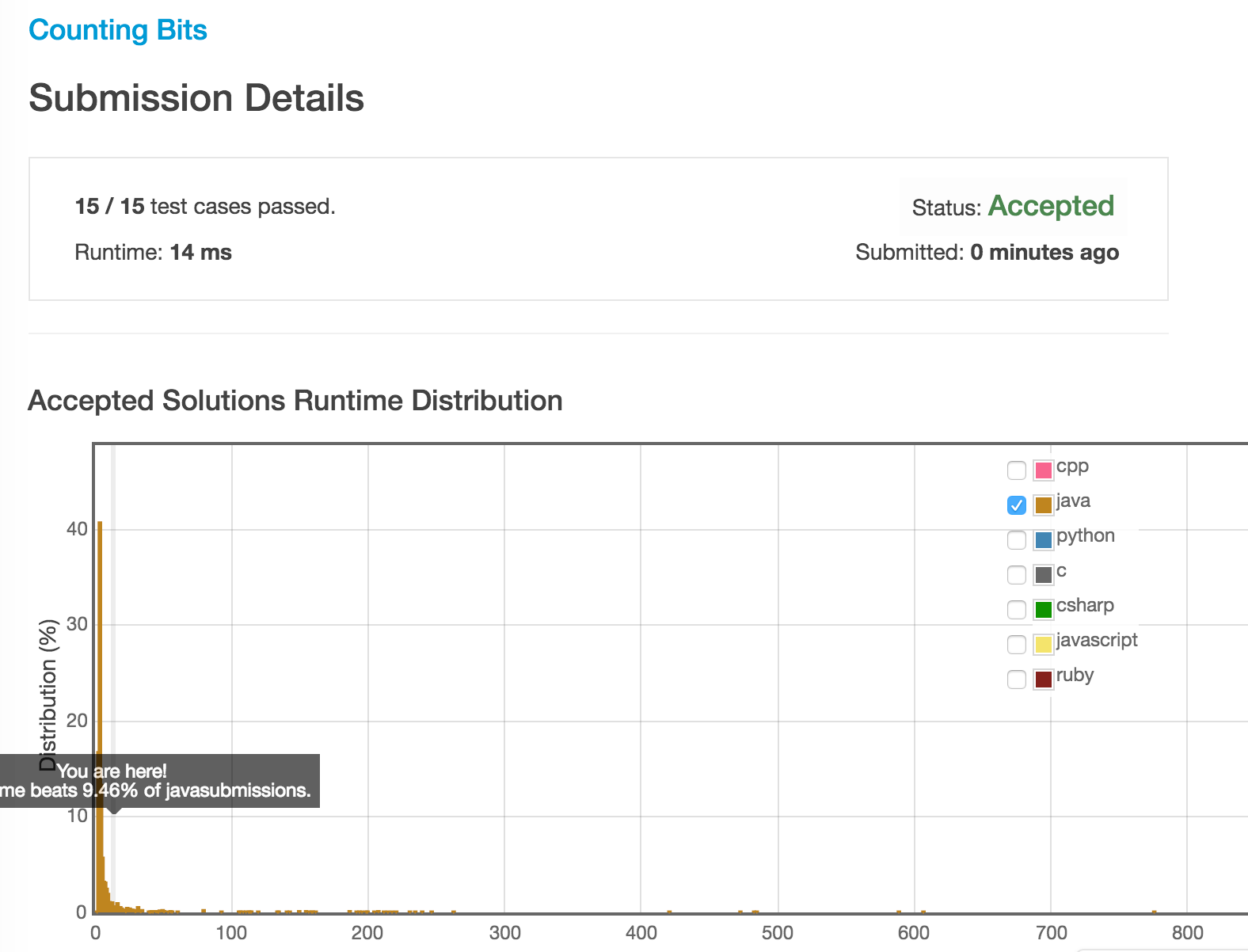
代码：

public class CountingBits {
    public int[] countBits(int num) {
        int[] cache = new int[num + 1];
        int begin = 1;
        int count = 0;
        while (begin <= num) {
            int i = 0;
            for (; i < Math.pow(2, count); i++) {
                if (begin + i <= num) {
                    cache[begin + i] = cache[i] + 1;
                } else {
                    return cache;
                }
            }
            begin = begin + i;
            count++;
        }
        return cache;
    }
}