图形学学习 TOPIC 1 Geometry&Representation

本文写作动机主要在于老师上课中英文交杂，听不懂的太多QwQ
主要用于个人学习和整理

Geometry

Basic Elements

scalars

vectors

-direction(方向)
-magnitude(大小)

（1）operations:
(a) inverse（取相反）
(b) be multipiled by a scalar
(c）zero vector: undefined orientation
(d) sum of two vectors is vector
（减法这里本质就是inverse+sum）

（2）Linear Vector Spaces
本质为向量的集合
operations：
上面的(b)(d)

（3）向量空间不适合几何
因为没有position

points

Location in space

（1）operations : between points and vectors
(a) v=P-Q
(b) P=v+Q
(v:vector P.Q:points)

Affine Spaces(仿射空间)

Point + a vector space

operations

标量
（a）标量间的运算
向量
（b）标量x向量
（c）向量加法（含减法）
点
（d）点+向量=点 点-点=向量
（e）定义：1·P=P
（f）定义：0·P=$\vec{0}$

我们看到，在定义中没有Point类型的加减运算，也没有scalar*point这类运算。
但是实际中，我们常常见到${\alpha }_1{p}_1+{\alpha }_2{p}_2$这样的公式。首先说明，这类公式是有意义的，原因在于它们的出现是由point+vector这类运算推导出来的，具体可以接着往下看，会逐渐明白的。

Rays and Line Segments

P( a) = Q + a (R-Q)=Q+av
=aR + (1-a)Q
（点=点+向量–>点=点+点）

Convexity

凸：当且仅当 P.Q属于该多边形，但是线段PQ不完全属于该多边形

Affine Sums(仿射和)

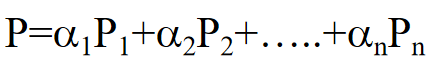
P1、P2…都是仿射空间中的点，

（1）上式中的P是point 当且仅当 右式系数和为1

证明：
$$\begin{gathered} P={\alpha }_1{P}_1+{\alpha }_2{P}_2+...+{\alpha }_n{P}_n; \\ \iff \\ P={\alpha }_1(P_1-P_2)+({\alpha }_1+{\alpha }_2)(P_2-P_3)+({\alpha }_1+{\alpha }_2+{\alpha }_3)(P_2-P_3)+... \\ +({\alpha }_1+...+{\alpha }_n)(P_{n-1}-P_n)+({\alpha }_1+...+{\alpha }_n)P_n; \\ \because Point-Point=VectorScalar\ast Vector=Vector \\ \therefore 令({\alpha }_1+...+{\alpha }_i)(P_i-P_{i+1})={\vec{V}}_i \\ \therefore P={\vec{V}}_1+{\vec{V}}_2+...+{\vec{V}}_{n-1}+({\alpha }_1+...+{\alpha }_n)P_n \\ \because Vector+Vector=Vector \\ \therefore 令{\vec{V}}_1+{\vec{V}}_2+...+{\vec{V}}_{n-1}=\vec{V} \\ \therefore P=\vec{V}+({\alpha }_1+...+{\alpha }_n)P_n \end{gathered}$$
$$\begin{gathered} \Rightarrow P是Point则右式系数和为1 \\ \because ({\alpha }_1+...+{\alpha }_n)P_n=P-\vec{V}且P是Point \\ \therefore ({\alpha }_1+...+{\alpha }_n)P_n是Point \\ \because 1\cdot Point=Point \\ \therefore ({\alpha }_1+...+{\alpha }_n)=1 \end{gathered}$$
$$\begin{gathered} \Leftarrow 右式系数和为1则P是Point \\ \because ({\alpha }_1+...+{\alpha }_n)=1且P_n是Point \\ \therefore P^{\prime }=({\alpha }_1+...+{\alpha }_n)P_n=1\cdot P_n=P_n \\ \therefore P=\vec{V}+P^{\prime } \\ \therefore P是Point \end{gathered}$$

（2）若a1,a2,…系数都 ≥0 ，则我们能够获得由P1,P2…构成的凸包

证明：（待更新）

planes

一个平面可以由一个点和两个向量或三个点定义

Representation

到目前为止，我们已经能够在不使用任何参考系(如坐标系)的情况下处理几何实体。但是在描述点的时候，我们仍需要一个坐标系。

Dimension

在向量空间中，线性无关向量的最大数目是固定的，称为空间的维数

Representation

注意，这种表示是关于一个特定的基的

Frames

（这里没有读懂）

homogeneous coordinate（齐次坐标系）

起因在于Points和vector会出现confuse
并且一个三维矩阵无法表示空间中的所有变换(见TOPIC 3)
齐次坐标是所有计算机图形系统的关键

（1）所有的标准变换(旋转，平移，缩放)都可以通过使用4 × 4矩阵的矩阵乘法来实现
（2）对于正交观察，我们可以保持vector的w=0，point的w=1

二维坐标系到三维齐次坐标的变换：
$$\begin{gathered} (X,Y,w)-->(x,y):x=\frac{X}{w},y=\frac{Y}{w} \\ (x,y)-->(X,Y,w):w=1,X=x,Y=y \end{gathered}$$

齐次坐标的意义

无穷远处的点在欧氏空间中无法具体展示。
在投影空间中，平行线会在无穷远处相遇，但在欧氏空间中却做不到。
因此此处引入齐次坐标。

（上图参考：知乎：齐次坐标ikuku回答）

任何N维度齐次坐标，只要W不为0，都可以通过将每一个分量除以W来转换到 W=1的向量, 然后获得其N-1维的欧式空间的点值。

而当W=0时，这个坐标表示无限长的一个向量，通常表示N-1维的矢量。

（这里我有一点没有明白，我懂得w=0表示无穷远处一个点，但是为什么向量可以用w=0表示没有想明白）

Change of Coordinate Systems

坐标系的转化

三维坐标系

其中a是w在第一个坐标系（v1,v2,v3）中的representation，b是w在(u1,u2,u3)中的representation。

齐次坐标系

Summary

新坐标系返回旧坐标系：
$$\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]=\left[\begin{array}{cccc}{X}_1^{\prime }& Y_1^{\prime }& Z_1^{\prime }& Q_{0x}\\ X_2^{\prime }& Y_2^{\prime }& Z_2^{\prime }& Q_{0y}\\ X_3^{\prime }& Y_3^{\prime }& Z_3^{\prime }& Q_{0z}\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\\ 1\end{array}\right]$$

Affine Transformations

（1）每个线性变换都等价于坐标系中的变化
指坐标系中的几何体、点、向量的变换，都可以看作是坐标系的转动
（2）每个仿射变换都保留直线
（这里没有懂）
（3）然而，一个仿射变换只有12个自由度，因为矩阵中的4个元素是固定的，并且是所有可能的4x4线性变换的子集

The World and Camera Frames

Moving the Camera