MIT算法导论-第二讲-渐进符号，递归及解法

1.渐进符号

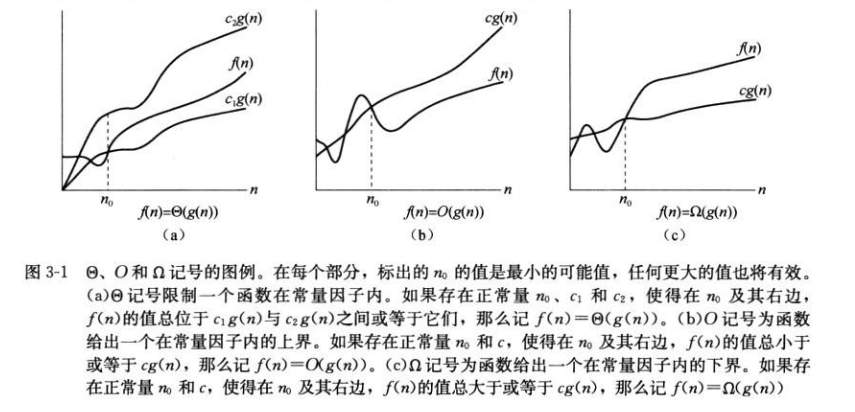
1. Θ符号，f(n) = Θ(g(n))，表示f(n)的复杂度既大于等于*g(n)的复杂度，又小于等于g(n)的复杂度，即于g(n)的复杂度相当*。
2. O符号，f(n) = O(g(n))，表示f(n)的复杂度最多与g(n)一个数量级，即小于等于。

3. Ω符号，f(n) = Ω(g(n))，f(n)的复杂度最少与g(n)一个数量级，即大于等于。
   

4. o符号，f(n) = o(g(n))，表示f(n)的复杂度要比g(n)的数量级小，即小于。
   例如2n = o(n^2) ,但是2n^2 != o(n^2)

5. ω符号，f(n) = ω(g(n))，表示f(n)的复杂度要比g(n)的数量级大，即大于。

---

2.递归式

算法设计中经常会用到递归，利用递归式的方法可以清晰地显示算法的整个过程，而对于分析算法