个人项目实战-四则混合运算

最新推荐文章于 2024-05-05 00:28:33 发布
最新推荐文章于 2024-05-05 00:28:33 发布
阅读量875 收藏 4
点赞数
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qing_tian0070/article/details/88826299
版权

代码仓库地址：https://dev.tencent.com/u/qingYinGuo/p/software_homework/git

测试效果见result.txt文件

一、 需求分析与功能设计

任务1：

    使用JAVA编程语言，独立完成一个3到5个运算符的四则运算练习的软件。

软件基本功能要求如下：

  • 程序可接收一个输入参数n，然后随机产生n道加减乘除（分别使用符号+-*÷来表示）练习题，每个数字在 0 和 100 之间，运算符在3个到5个之间。
  • 每个练习题至少要包含2种运算符。同时，由于小学生没有分数与负数的概念，你所出的练习题在运算过程中不得出现负数与非整数，比如不能出 3÷5+2=2.6，2-5+10=7等算式。
  • 练习题生成好后，将你的学号与生成的n道练习题及其对应的正确答案输出到文件“result.txt”中，不要输出额外信息，文件目录与程序目录一致。
  • 当程序接收的参数为4时，以下为一个输出文件示例。

2018010203

13+17-1=29

11*15-5=160

3+10+4-16=1

15÷5+3-2=4

软件附加功能要求如下：(请有余力的同学完成)

  • 支持有括号的运算式，包括出题与求解正确答案。注意，算式中存在的括号数必须大于2对，且不得超过运算符的个数。
  • 扩展程序功能支持真分数的出题与运算（只需要涵盖加减法即可），例如：1/6 + 1/8 + 2/3= 23/24。注意在实现本功能时，需支持运算时分数的自动化简，比如 1/2+1/6=2/3，而非4/6，且计算过程中与结果都须为真分数。

二、 设计实现

项目的目录结构

 

 

  • Main类：主类，负责接收命令行的参数并启动程序。
  • GenerateFile类：创建文件类，负责每次出题类型并产生result.text文件，将学号与练习题写入文件。
  • GenerateFormula类：式子类，负责根据调用产生各类型的式子，简单四则运算、带括号的四则运算、真分数加减运算。
  • Calculator类：计算类，负责各种计算，含有结果运算、有条件产生减数、有条件产生除数、有条件产生分子、有条件产生分母、判断数的大小、求取最大公因数、求取最小公倍数、分数相加、分数相减等方法。

二、收获点

1.利用js的eval函数对生成的四则运算进行计算，简化了很多的代码

static ScriptEngine scriptEngine=
			new ScriptEngineManager().getEngineByName("JavaScript");
	public static Object calulate(String str){
		//为什么定义时一定要带上=0？
		Object result=0;
		try {
			 result=scriptEngine.eval(str);
		} catch (ScriptException e) {
			e.printStackTrace();
		}
		return result;
	}

2.最小公倍数简单算法的实现

	//最小公倍数
	
	public static int lcm(int num1,int num2){
		int lcm=num1;
		while(lcm%num1!=0||lcm%num2!=0){
			lcm++;
		}
		return lcm;
		
	}

 3.对小数的判断

//  对于小数的判断
	public static boolean decimals(String result){
		boolean hasDecimals=false;
		if (result.contains(".")){
			hasDecimals=true;
			
		}
		return hasDecimals;
	}

4.最大公因数

//  对于小数的判断
	public static boolean decimals(String result){
		boolean hasDecimals=false;
		if (result.contains(".")){
			hasDecimals=true;
			
		}
		return hasDecimals;
	}

三、整个项目最麻烦也最关键的生成计算式的类

public class GenerateFormula {
	
	//形成运算式子
	
	public static String simpleArithmetic(){
		//标准形式
		char[] stanSympol = new char[] { '*', '+', '/', '-' };
		//输出形式
		char[] outSympol = new char[] { '*', '+', '÷', '-' };
		String str1="";
		String str2="";
		//生成符号的个数
		int symbolCount= (int) (Math.random()*3+3);
		//生成数字数组
		int num[]=new int[symbolCount+1];
		for(int i=0;i<=symbolCount;i++){
			num[i]= (int) (Math.random()*100+1);
		}
		//生成符号数组
		//符号的个数比数字少一
		int symbol[]=new int[symbolCount];
		for (int i=0;i<symbolCount;i++){
			if (i>0&&symbol[i-1]==3){
				
				//减号之后必须是加号
				
				symbol[i]=1;
			}
			else if(i>0&&symbol[i-1]==2){
				//除号之后必须是乘法或加法
				symbol[i]= (int) (Math.random()*2);
			}
			else {
				symbol[i]= (int) (Math.random()*4);
			}
			str1+=String.valueOf(num[i])+String.valueOf(stanSympol[symbol[i]]);
			str2+=String.valueOf(num[i])+String.valueOf(outSympol[symbol[i]]);
			
			if (symbol[i]==2){
				num[i+1]=Calculator.divisor(num[i],num[i+1]);
			}
			else if(symbol[i]==3){
				num[i+1]=Calculator.subtractor(num[i],num[i+1]);
			}
		}
		int j=0;
		while (j<(symbolCount-1)&&symbol[j]==symbol[j+1]){
			j++;
		}
		if(j==(symbolCount-1)){
			return simpleArithmetic();
		}
		else {
			str1+=String.valueOf(num[symbolCount]);
			str2+=String.valueOf(num[symbolCount]);
			return str2+"="+Calculator.calulate(str1);
		}
		
		
	}
	
	//生成分数
	public static String fraction(){
		char[] symbol={'+','-'};
		String str="";
		int symCount= (int) (Math.random()*3+3);
		//分子
		int x[]=new int[symCount+1];
		//分母
		int y[]=new int[symCount+1];
		//符号集
		int z[]=new int[symCount];
		//中间运算结果
		int mid[]=new int[2];
		//生成分数数字集
		for (int i=0;i<=symCount;i++){
			x[i]= (int) (Math.random()*35+1);
			y[i]=Calculator.stfraction(x[i]);
		}
		mid[0]=x[0];
		mid[1]=y[1];
		//生成符号集
		for (int i=0;i<symCount;i++){
			z[i]= (int) (Math.random()*2);
			if (z[i]==0){
				int a1[]=new int[2];
				a1=Calculator.addFraction(mid[0],mid[1],x[i+1],y[i+1]);
				//中间的运算结果也要为真分数
				if (a1[0]>=a1[1]){
					z[i]=1;
				}
				else {
					mid=a1;
				}
			}
			if (z[1]==1){
				int a1[]=new int[2];
				a1=Calculator.subFraction(mid[0],mid[1],x[i+1],y[i+1]);
				if (a1[0]<0){
					x[i+1]=Calculator.stfraction2(mid[0],mid[1]);
					y[i+1]=mid[1];
					a1=Calculator.subFraction(mid[0],mid[1],x[i+1],y[i+1]);
				}
				mid=a1;
			}
			str+=String.valueOf(x[i])+"/"+String.valueOf(y[i])+String.valueOf(symbol[z[i]]);
		}
		int j=0;
		while (j<(symCount-1)&&z[j]==z[j+1]){
			j++;
		}
		if (j==(symCount-1)) {
			return fraction();
		}
		else {
			str+=String.valueOf(x[symCount])+"/"+String.valueOf(y[symCount]);
			return str+"="+mid[0]+"/"+mid[1];
		}
		
	}
	//随机产生括号的四则运算
	
	public static String addBracket() {
		//标准形式
		char[] stanSympol = new char[]{'*', '+', '/', '-'};
		//输出形式
		char[] outSympol = new char[]{'*', '+', '÷', '-'};
		String str1 = "";
		String str2 = "";
		//生成括号的个数
		int bracket = 0;
		//未匹配的左括号的个数
		int bracket_left = 0;
		//符号个数
		int symCount = (int) (Math.random() * 3 + 3);
		//存储符号的数组
		int[] symbol = new int[symCount];
		//存储数字的数组
		int[] num = new int[symCount + 1];
		//随机产生数字
		for (int i = 0; i <= symCount; i++) {
			num[i] = (int) (Math.random() * 100 + 1);
		}
		//随机生成符号
		for (int j = 0; j <= (symCount - 1); j++) {
			symbol[j] = (int) (Math.random() * 4);
		}
		//形成运算式
		for (int i = 1; i <= (symCount - 1); i++) {
			//减数时防止产生负数
			if (symbol[i] == 3) {
				num[i] = Calculator.subtractor(num[i - 1], num[i]);
			} else if (symbol[i] == 2) {
				num[i] = (int) (Math.random() * 100 + 1);
			}
			str1 += num[i];
			str2 += num[i];
			int bracket_left1 = bracket_left;
			for (int j = 0; j < bracket_left1; j++) {
				if ((int) (Math.random() * 3) > 1) {
					bracket_left--;
					str1 += ")";
					str2 += ")";
				}
			}
			str1 += stanSympol[symbol[i]];
			str2 += outSympol[symbol[i]];
			
			if (((bracket * 2) <= symCount) && (((int) (Math.random() * 9)) > 1)) {
				str1 += "(";
				str2 += "(";
				bracket++;
				bracket_left++;
				str1 += num[++i];
				str2 += num[i];
				str1 += stanSympol[symbol[i - 1]];
				str2 += outSympol[symbol[i - 1]];
				
				
			}
		}
		int k = 0;
		while (k != symCount) {
			if (symbol[k] == 3) {
				num[k + 1] = Calculator.subtractor(num[k], num[k + 1]);
			} else if (symbol[k] == 2) {
				num[k + 1] = (int) (Math.random() * 100 + 1);
			}
			str1 += num[k];
			str2 += num[k];
			str1 += stanSympol[symbol[k]];
			str2 += outSympol[symbol[k]];
			k++;
		}
		if (symbol[symCount - 1] == 3) {
			num[symCount] = Calculator.subtractor(num[symCount - 1], num[symCount]);
		}
		str1 += num[symCount];
		str2 += num[symCount];
		while (bracket_left != 0) {
			str1 += ")";
			str2 += ")";
			bracket_left--;
		}
		str2 += "=";
		String result = String.valueOf(Calculator.calulate(str1));
		if (Calculator.decimals(result) || result.contains("Infinity")) {
			return addBracket();
		} else if (bracket >= 2) {
			int result1 = Integer.parseInt(result);
			if (result1 < 0) {
				return addBracket();
			} else {
				return str2 + result;
			}
		}
		else {
			return addBracket();
		}
		
	}
}

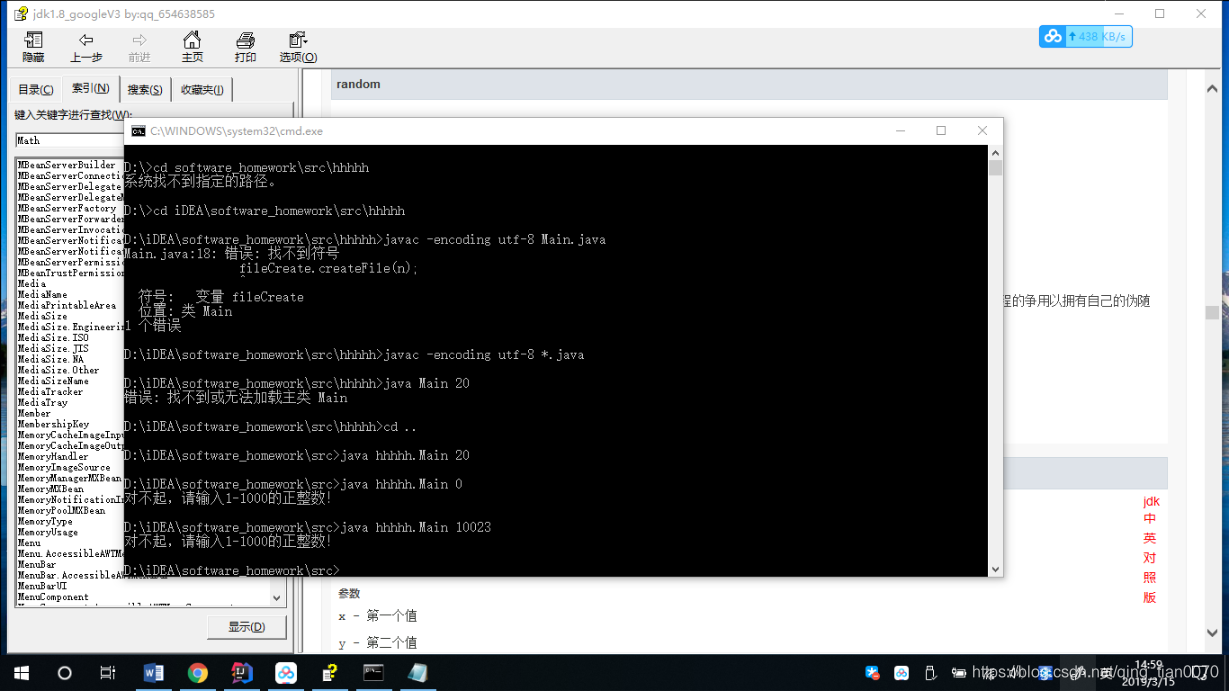
5.本地命令行运行报错

a.中文乱码

b.编译问题

四、总结

这个项目我开始想的时候式很简单的，但是真正写起来才发现并不如我所想的那样简单。开始写简单四则运算的时候，我就开始要写代码的数量发愁，偶然发现了eval（）方法，心底真的式发出了感叹，居然会有如此神奇的算法，编程世界的前辈们真的是太优秀啦！

有了这种方法的帮助，四则运算也很快的就完成了。对于附加功能的实现，我是借鉴了学长学姐的方法，当然。我相信只要给我时间，拥有耐心，我相信，我也是可以成功实现的。前辈们的方法好则好矣，却是使我减少了思考过程的探险，少了许多项目完成时的欣喜。

qing_tian0070
关注
让多个 Agent 协同工作：PettingZoo 多智能体项目实战
努力分享一些人工智能相关的知识干货！
04-10 734
当你搭建好一个 Agent，还不足以应对真实世界的复杂任务。 真正强大的 AI 系统，往往是多个 Agent 各司其职、互相协作： 有的负责感知，有的负责判断，有的负责行动，有的负责校验。 **本章我们将首次进入多智能体系统的动手实战阶段，基于强化学习领域中广泛使用的 PettingZoo 多 Agent 环境，亲自训练和运行一个协作型智能体系统。** > 从环境选择、智能体定义、训练算法，到策略可视化与代码封装，一步步带你从 0 落地一个真正的多 Agent 协同系统。
Python全栈（八）Flask项目实战之6.前台注册功能开发
CUFEECR的博客
06-24 1427
后台的整体页面和基本架构已经搭建好，转到前台开发。首先对前台用户模型进行定义，属性比后台用户更多，在manage.py中进行映射。在相应目录下创建模板文件、css和js文件，视图文件中实现视图类；再实现图形验证码类，用于生成带随机验证码和干扰线的图片。在试图文件中实现生成随机图片验证码并添加到注册页，再通过JS控制点击更换图片。发送短信验证码一般通过使用第三方服务、调用SDK实现，并在公共文件夹视图文件实现具体功能。在模板中加入CSRF保护，通过表单对注册请求进行验证，还要对JS文件加密来提高安全性。
C语言 四则混合运算程序
07-31
一个简单的程序，但是很实用，适合C语言初学者
四则运算练习题
weixin_33968104的博客
04-19 207
#include<stdlib.h> #include<stdio.h> #include<time.h> #include"math.h" #include<conio.h> void main() { int a,b,c,d,e,r,i,v,an; char ch1[4]={'+','-','*','/'}...
四则混合运算
lypl emmmm…
03-26 840
1 程序简要图解 2 分块说明 1）生成普通算式并计算 生成：生成第一个运算数 -> for（auto i = 1：cnt）先生成一个运算符，再生成一个运算数（ps：这样可以保证避免出现连乘连除、运算过程为负数、不能整除的情况）-> 将该序列转化为String 以便最后输出 string tmp=""; memset(num,-1,sizeof(num)); //产...
小学四则运算练习（JavaScript版）
Cream_Cicilian的博客
04-02 2608
使用语言：JavaScript需求分析：程序可接收一个输入参数n，然后随机产生n道加减乘除（分别使用符号+-*÷来表示）练习题，每个数字在 0 和 100 之间，运算符在3个到5个之间 每个练习题至少要包含2种运算符。不能存在分数、负数与非整数。 练习题生成好后，将你的学号与生成的n道练习题及其对应的正确答案输出到文件“result.txt”中，不要输出额外信息，文件目录与程序目录一致功能设计：
四则混合运算表达式分析程序----C#递归分析版
08-26
四则混合运算表达式分析程序----C#递归分析版
kubernetes混合云平台运维实战项目分享
weixin_38924998的博客
01-13 465
hi;大家好，今天是周六杭州天气不错，有时间写一篇博客分享一下最近在做的兼职项目架构，不涉及公司名称及业务，只分享技术架构。
计算机视觉项目实战-背景建模与光流估计（目标识别与追踪）_计算机视觉在不同光源下采集数据的像素值变化的规律
最新发布
2401_84185182的博客
05-05 889
熟悉OpenCV的小伙伴们都知道一点就是视频是由一帧一帧的图像组合而成，那么当我们传进来一个摄像头录制的图像的时候（因为摄像头录制的较为稳定），我们是不是也可以做这样的一件事：检测到那些物体或者说那些人在运动，那些物体没有在运动。也就是我们所谓的哪些是前景，那些是背景。那么我们就来具体看看背景建模都有那些方法。
vue项目实战精粹汇总
趣谈前端
02-09 3473
前言vue作为前端主流的3大框架之一，目前在国内有着非常广泛的应用，由于其轻量和自底向上的渐进式设计思想，使其不仅仅被应用于PC系统，对于移动端，桌面软件（electronjs）等也有广泛...
Java综合程序设计——计算器（实现运算符优先级的四则混合运算）
06-19
一个计算器，有多种功能，如取对数、求平方根。最重要的是利用堆栈算法实现运算符优先级。
四则混合运算（简单计算器）C语言实现
11-15
给出四则混合运算的详细实现，代码较为全面给出了包括错误检查等各个发面的问题
汇编语言课程设计报告—四则运算（附流程图、源代码）
03-28
四则运算：从键盘输入一个十进制两位数的四则运算表达式，如23*56－（8*19）/6＋67－8＝，编程计算表达式的值，输出十进制结果（有可能是三位或四位十进制）,＋－*/位置任意。并能反复执行直道对“还要继续吗？（y/n）”之类的提示回答“n”或“N”为止。 完整的汇编语言课程设计实验报告，并附有源代码
四则运算测试程序（供小学生测试非常实用）
11-24
随即产生两个数字，系统规定的是10之内的！ 由用户输入答案，程序判断正确与否，并统计正确数，错误数，和正确率~~
个人项目实战-四则混合运算-项目总结
脑袋呆呆
03-21 631
个人项目实战-四则混合运算 代码仓库地址：https://git.dev.tencent.com/Woohxe/fourArithmetic.git 测试效果见result.txt文件 一、 需求分析与功能设计 接收一个输入参数n，随机产生n道加减乘除练习题，分别使用符号±*÷来表示 每个数字在 0 和 100 之间 运算符在3个到5个之间并且每道练习题至少要包含2种运算符 运算过...
实现简单的四则混合运算
gaomingjava的博客
05-27 463
package cn.gao.algorithm2.service; import java.util.ArrayList; /** * 四则混合运算运算，如给定一个字符串"a+b*c-d/e"，计算该表达式值 * @param args */ public class Test11 { public ArrayList&lt;Integer&gt; objectLi...
结对编程——四则混合运算生成
tang151的博客
04-06 1083
一、这是一次对结对编程的尝试，我和队友经历思考之后成功完成代码，运用了工厂模式，结果如下： 这是一则运算的实体类 package com.lhw;import java.util.HashSet; import java.util.Random; import java.util.Set;public class Operation { private Integer number1
出300个四则运算练习题
weixin_30687051的博客
03-08 229
产生300个四则运算的java实现方法： 修改后代码： 转载于:https://www.cnblogs.com/zmbeijixing/p/8526606.html
PHP Laravel个人博客开发实战教程
开发者可以通过本项目学习如何使用这些技术来搭建一个功能完善的个人博客系统，包括用户认证、文章发布、评论互动等模块。 知识点七：文件结构说明 提供的压缩包名为"基于PHP+Laravel+Bootstrap+JQuery+MySQL个人...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值