标准C++复数运算类详解及使用例程

    在C++中复数运算可以通过两种方式来实现：

    1）标准C++复数运算库：complex<typedef> ObjectName(realPart, imagePart);

    2）自定义复数运算类：包括复数的实部、虚部、四则运算、模运算、共轭等。

    后者可以根据需要自己定义，关于类的定义这里不再说明，具体的功能可以根据自己的需要去实现。这里介绍C++标准的复数运算类complex，网上已经有一些关于complex类的简单介绍，但大多都是比较粗略的说明，并没有提供完整而详细的介绍。这里参考了网上的一些资源，首先介绍complex类的定义，包括：对象的构造方法、算术运算、赋值运算符、指数运算、对数运算、幂运算、三角函数运算、输入输出重载等，然后给出了一个使用例程，用于对其使用方法的总结用户总结。

一、complex类简介

    C++复数运算由标准C++复数运算库(complex number mathematics library)来实现。complex类定义了标准的输入输出运算、算是运算、关系运算和赋值运算，同时还包括指数运算、对数运算、幂运算、平方根、三角函数(正弦，余弦，双曲正弦，双曲余弦)等，还包括笛卡尔坐标系到极坐标系转换的函数。

二、文件包含

1、 #include <complex.h>

2、 #include <math.h>

三、构造方法

1、complex为模板类，因此在定义一个复数时需要制定变量类型，如complex<double> cm(1,1);

2、定义时实部和虚部参数可以使用变量，如：

double a = 1;
double b = 1;
complex<double> cm(a, b);

3、以下定义均合法：

    a) complex(): complex<double> c1;// c1 = (0,0);

    b) complex(double real, double<double> imag = 0.0): complex c2(1.0);// c2 = (1.0,0);

    c) complex<double> c3 = 3.4; // c3 = (3.4,0);

    d) complex c4 = 3.4 + complex(1.2, 3.5);

四、笛卡尔坐标系和极坐标系下有关函数

1、real();: friend double real(complex a);

2、 img();: friend double imag(complex a);

3、 abs();: friend double abs(complex a);

4、 norm();: friend double norm(complex a);

5、 arg();: friend double arg(complex a);

6、 conj();: friend complex conj(complex a);

7、 polar();: friend complex polar(double r,double t);

示例：

d = real(a);// 返回复数a的实部
d = imag(a);// 返回复数a的虚部
d = abs(a);// 返回复数a的模值/幅值
d = norm(a);// 返回复数a的模值平方
d = arg(a);// 返回复数a的幅角
z = conj(a);// 返回复数a的共轭复数
z = polar(r,t);// 复数的极坐标定义方式，r为幅值，t为幅角

五、指数、对数、幂、平方根运算函数

1、 exp(); friend complex exp(complex a);

2、 log(); friend complex log(complex a);

3、 pow(); 四种

        a) friend complex pow(double a, complex b);

        b) friend complex pow(complex a, int b);

        c) friend complex pow(complex a, double b);

        d) friend complex pow(complex a,complex b);

4、 sqrt();friend complex sqrt(complex a);

六、三角关系运算函数

1、 sin(); friend complex sin(complex a);

2、 cos(); friend complex cos(complex a);

3、 sinh(); friend complex sinh(complex a);

4、 cosh(); friend complex cosh(complex a);

七、运算符重载

    运算符重载包括：+、-、*、/（包括+=、-=、*=、/=）、==、!=、<<、>>

八、使用例程

1、开发环境：Win7 (X64) / VS2010

2、创建新项目，编写代码如下：

#include <iostream>
#include <complex>
#include <math.h>

using namespace std;

void main()
{
	// 复数类对象定义
	cout << "复数类对象定义" << endl;
	double r = 1.0;
	double x = 1.0;
	complex<double> c1;
	complex<double> c2(1,1);
	complex<double> c3(r,x);
	complex<double> c4 = 2.0;
	complex<double> c5 = c4 + complex<double>(2,1);

	cout << "c1 = " << c1 << endl;
	cout << "c2 = " << c2 << endl;
	cout << "c3 = " << c3 << endl;
	cout << "c4 = " << c4 << endl;
	cout << "c5 = " << c5 << endl << endl;

	// 笛卡尔坐标系和极坐标系下有关函数
	cout << "笛卡尔坐标系和极坐标系下有关函数" << endl;
	cout << "c5实部real：" << c5.real() << endl;
	cout << "c5虚部imag：" << c5.imag() << endl;
	cout << "c5模值abs：" << abs(c5) << endl;
	cout << "c5模值平方norm：" << norm(c5) << endl;
	cout << "c5幅角arg：" << arg(c5) << endl;
	cout << "c5共轭复数conj：" << conj(c5) << endl;
	complex<double> z = polar(1.0, 3.14/6);
	cout << "复数极坐标定义polar：" << z << endl << endl;

	// 运算符重载，四则运算
	cout << "运算符重载，四则运算" << endl;
	cout << "c2 + c5 = " << c2 + c5 << endl;
	cout << "c2 - c5 = " << c2 - c5 << endl;
	cout << "c2 * c5 = " << c2 * c5 << endl;
	cout << "c2 / c5 = " << c2 / c5 << endl << endl;

	system("pause");
}

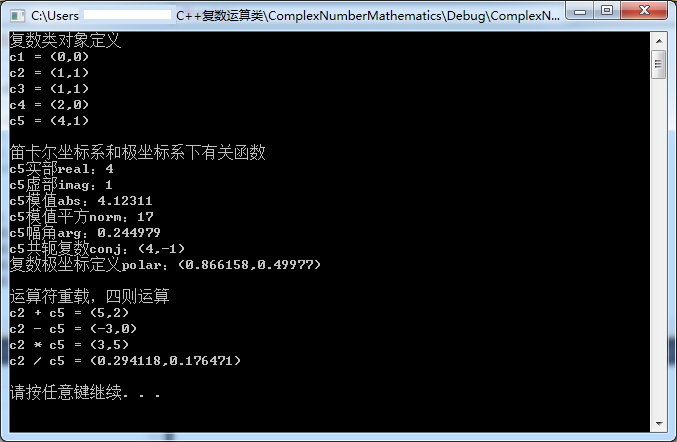
3、运行结果如图1所示：

图1

参考：

1）http://blog.chinaunix.net/uid-20559667-id-1924707.html

2）http://blog.csdn.net/qhs1573/article/details/12254205