主成分分析-PCA

主成分分析是一种常用的降维方法，它可以帮助我们识别最重要的多个特征，去除数据中的噪声，同时还能够降低计算量。本篇文章将从原理推导、python实现以及案例分析三个方面进行讲解。

原理推导

通常来讲，我们可以从两个方面来看待PCA要做的事情，一者是最大化投影方差，一者是最小化原始数据到投影平面上的距离平方和。

最大化投影方差

我们先来看如何从方差的角度进行PCA的推导。首先，我们要明白为什么说PCA降维后要尽可能最大化投影方差呢？这里可以设想一种极限的情况，如果数据经过PCA降维后的投影方差为0，此时所有的数据都聚集于一个位置，也就失去了数据之间的差异性，这样的降维数据无法提供有价值的信息，因此我们要尽可能最大化投影方差。
我们还可以从信号处理的角度来理解这个问题，信号具有较大的方差，噪声具有较小的方差，信号与噪声之比称为信噪比。信噪比越大意味着数据质量越好，反之则越差。因此我们要想让投影后的数据质量好，也必须最大化投影方差才行。
那么如何计算方差呢？对于一组给定的数据点$v_1,v_2,...,v_n$，每个点都是列向量，中心化后的表示为$$x_1,x_2,...,x_n=v_1-u,v_2-u,...,v_n-u$$其中$u=\frac{1}{n}{\sum }_{i=1}^n{v}_i$ 我们的目标就是找到一个投影方向w，使得$x_1,x_2,...,x_n$在w上的投影方差尽可能大，由于投影之后的坐标为$x_i^{T}w$，均值为0，因此投影后的方差可以表示为
$$\begin{array}{rl}D(x)& =\frac{1}{n}\sum _{i=1}^n(x_i^{T}w{)}^2\\ & =\frac{1}{n}\sum _{i=1}^n(x_i^{T}w{)}^T(x_i^{T}w)\\ & =\frac{1}{n}\sum _{i=1}^n{w}^T{x}_i{x}_i^{T}w\\ & =w^T(\frac{1}{n}\sum _{i=1}^n{x}_i{x}_i^T)w\end{array}$$
其实$\frac{1}{n}{\sum }_{i=1}^n{x}_i{x}_i^T$就是样本的协方差矩阵，我们将之写作$\sum$，另外由于w是单位向量，因此有$w^{T}w=1$。因此整个问题可以表述为如下形式：
m a x { w T ∑ w } s . t . w T w = 1 \begin{aligned} &max\lbrace w^T\sum w\rbrace \\ &s.t. w^Tw=1 \end{aligned} ​max{wT∑w}s.t.wTw=1​
引入拉格朗日乘子，并对w求导令其等于0，便可以推导出$\sum w=\lambda w$
$$\begin{array}{rl}& L=w^T\sum w-\lambda (w^{T}w-1)\\ & \frac{\partial L}{\partial w}=2\sum w-2\lambda w=0\\ & \sum w=\lambda w\end{array}$$
此时，
$$\begin{array}{r}D(x)=w^T\sum w=\lambda \end{array}$$
从上式可知，x投影后的方差就是协方差矩阵的特征值。我们要找到最大的方差也就是协方差矩阵最大的特征值，最佳投影方向就是最大特征值对应的特征向量，而次佳投影方向则是第二大特征值对应的特征向量。至此，我们可以得到PCA的求解方法：

1. 将数据进行中心化处理
2. 计算样本协方差矩阵
3. 对协方差矩阵进行特征值分解，特征值从大到小排序
4. 取特征值前d大对应的特征向量$w_1,w_2,...,w_d$，通过以下映射将n维样本映射到d维
   $${\hat{x}}_i=\left[\begin{array}{c}{w}_1^T{x}_i\\ w_2^T{x}_i\\ ...\\ w_d^T{x}_i\end{array}\right]$$
   通过选取最大的d个特征值对应的特征向量，我们将方差较小的特征抛弃，使得每个列向量$x_i$被映射为d维列向量${\hat{x}}_i$，定义降维后的信息占比为
   $$\begin{array}{r}n=\sqrt{\frac{{\sum }_{i=1}^d{\lambda }_i^2}{{\sum }_{i=1}^n{\lambda }_i^2}}\end{array}$$

最小平方误差

我们也可以将PCA求解问题转化为一个回归问题，要让投影平面更好地拟合样本点，实质上就是让数据点到这个投影平面的距离平方和最小，相当于使用了平方损失函数。当然，我们也可以从另外一个方面去理解，每个样本点到投影平面的均值点距离是固定的（因为均值是0，相当于原点），如果最小平方误差，依据勾股定理，方差也就会最大。
数据集中每个点$x_k$到d维超平面D的距离为
$$distance(x_k,D)=||x_k-{\hat{x}}_k|{|}_2$$
其中${\hat{x}}_k$表示$x_k$在超平面D上的投影向量。如果该超平面由d个标准正交基 W = { w 1 , w 2 , . . . , w d } W=\lbrace w_1,w_2,...,w_d\rbrace W={w1​,w2​,...,wd​}构成，依据线性代数理论${\hat{x}}_k$可以由这组基线性表示
$${\hat{x}}_k=\sum _{i=1}^d(w_i^T{x}_k)w_i$$
因此PCA要优化的目标可写成
$$\begin{array}{r}argmin\sum _{k=1}^n||x_k-{\hat{x}}_k|{|}_2^2\\ s.t.w_i^T{w}_j={\delta }_{ij}=\{\begin{array}{c}1,i=j\\ 0,i\ne j\end{array}\end{array}$$
依据向量内积的性质，我们可以将距离展开
$$\begin{array}{rl}||x_k-{\hat{x}}_k|{|}_2^2& =(x_k-{\hat{x}}_k{)}^T(x_k-{\hat{x}}_k)\\ & =x_k^T{x}_k-2x_k^T{\hat{x}}_k+{\hat{x}}_k^T{\hat{x}}_k\end{array}$$
其中第一项与W无关，我们将${\hat{x}}_k$带入上式可得
$$\begin{array}{rl}{x}_k^T{\hat{x}}_k& =x_k^T\sum _{i=1}^d(w_i^T{x}_k)w_i\\ & =\sum _{i=1}^d(w_i^T{x}_k)x_k^T{w}_i\\ & =\sum _{i=1}^d{w}_i^T{x}_k{x}_k^T{w}_i\\ {\hat{x}}_k^T{\hat{x}}_k& =(\sum _{i=1}^d(w_i^T{x}_k)w_i{)}^T\sum _{i=1}^d(w_i^T{x}_k)w_i\\ & =\sum _{i=1}^d\sum _{j=1}^d((w_i^T{x}_k)w_i{)}^T(w_j^T{x}_k)w_j\end{array}$$
注意到，$w_i^T{x}_k$和$x_j^T{x}_k$都是数字。且当$i\ne j$时，$w_i^T{w}_j=0$，因此上式可写成
$$\begin{array}{rl}{\hat{x}}_k^T{\hat{x}}_k& =\sum _{i=1}^d(w_i^T{x}_k)(w_i^T{x}_k)\\ & =\sum _{i=1}^d{w}_i^T{x}_k{x}_k^T{w}_i\end{array}$$
其实，该值实际上就是矩阵$W^T{x}_k{x}_k^{T}W$的迹，于是上式还可化简为
$$\begin{array}{rl}||x_k-{\hat{x}}_k|{|}_2^2& =-tr(W^T{x}_k{x}_k^{T}W)+x_k^T{x}_k\end{array}$$
因此，整个优化目标可写成
$$\begin{array}{r}argmin\sum _{k=1}^n||x_k-{\hat{x}}_k|{|}_2^2=\sum _{k=1}^n-tr(W^T{x}_k{x}_k^{T}W)+x_k^T{x}_k\end{array}$$
依据矩阵乘法的性质${\sum }_k{x}_k{x}_k^T=X{X}^T$，上述优化问题转换为
$$\begin{array}{rl}& argmaxtr(W^{T}X{X}^{T}W)\\ & s.t.W^{T}W=I\end{array}$$
如果我们对W中的d个基依次求解，就会发现和最大方差理论的方法完全等价。

Python实现

当我们明白了PCA的原理和求解步骤之后，就可以很容易地使用python进行求解，下面给出求解代码：

def pca(data_mat, top_n_feat=9999999):  
    mean_vals = np.mean(data_mat, axis=0)  
    mean_removed = data_mat - mean_vals  
    # rowvar代表行还是列为属性，true是行，false是列  
    cov_mat = np.cov(mean_removed, rowvar=0)  
    eig_vlas, eig_vects = np.linalg.eig(cov_mat)  
    eig_val_ind = np.argsort(eig_vlas)  
    eig_val_ind = eig_val_ind[:-(top_n_feat + 1): -1]  
    # 结果是每列作为一个基向量  
    red_eig_vects = eig_vects[:, eig_val_ind]  
    # 去均值后的数据在d个主要特征向量上的投影
    low_dat_math = mean_removed * red_eig_vects  
    # 重建数据  
    recon_mat = (low_dat_math * red_eig_vects.T) + mean_vals  
    return low_dat_math, recon_mat

案例分析

sklearn接口初使用

先用一个简单的例子来看看Sklearn中关于PCA接口如何使用。我们先随机生成一份二维数据，并将之可视化：

import numpy as np
import matplotlib.pyplot as plt
rng = np.random.RandomState(1)
X = np.dot(rng.rand(2, 2), rng.randn(2, 200)).T
plt.scatter(X[:, 0], X[:, 1])
plt.axis('equal')

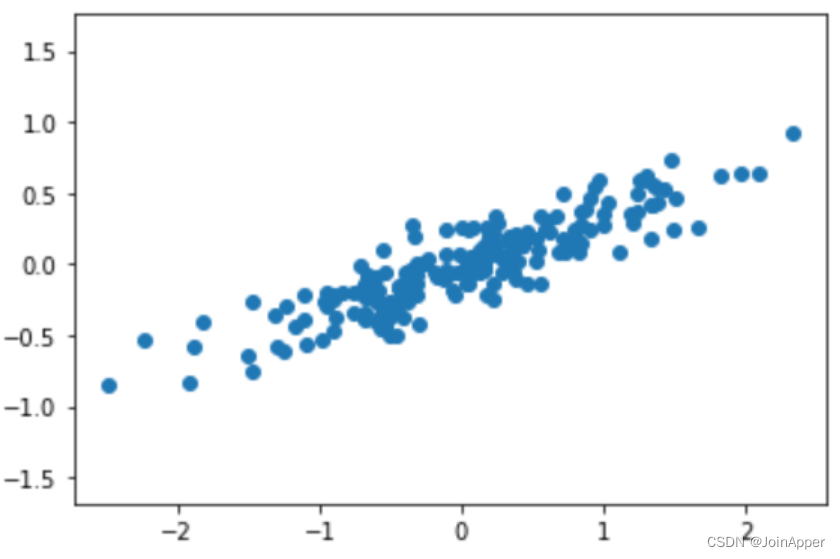
对该数据进行PCA降维处理，并绘制主成分的方向：

from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(X)
# pca降维后的主成分，每行代表一个特征向量
print(pca.components_)
# pca降维后的特征值方差
print(pca.explained_variance_)

# 绘制pca主成分的方向
def draw_vector(v0, v1, ax=None):
    ax = ax or plt.gca()
    arrowprops = dict(arrowstyle='->',
                     linewidth=2,
                     shrinkA=0, shrinkB=0)
    ax.annotate('', v1, v0, arrowprops=arrowprops)
    

plt.scatter(X[:, 0], X[:, 1], alpha=0.2)
for length, vector in zip(pca.explained_variance_, pca.components_):
    v = vector * 3 * np.sqrt(length)
    draw_vector(pca.mean_, pca.mean_ + v)
plt.axis('equal')

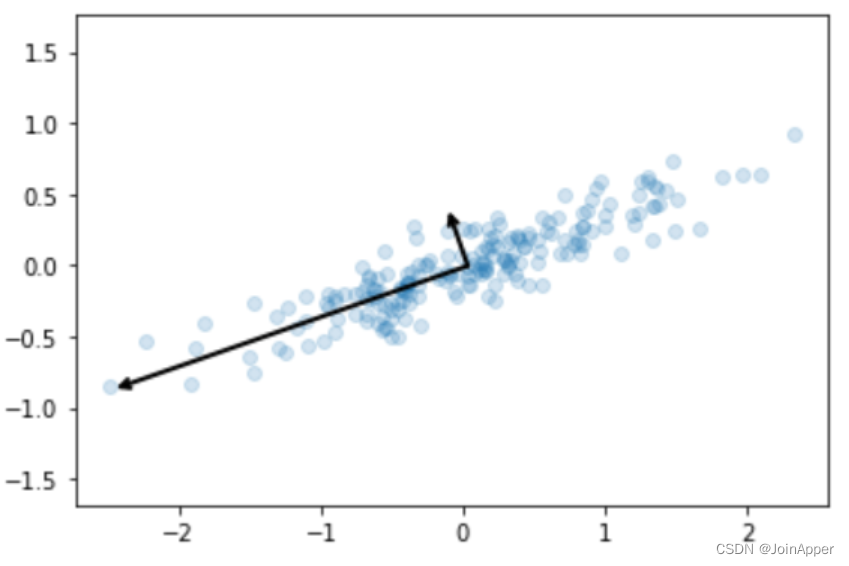
从图中我们可以看出每个主成分的重要程度，可以通过以下方式将数据投影到方差最大的主成分方向：

pca = PCA(n_components=1)
pca.fit(X)
X_pca = pca.transform(X)
X_new = pca.inverse_transform(X_pca)
plt.scatter(X[:, 0], X[:, 1], alpha=0.2)
plt.scatter(X_new[:, 0], X_new[:, 1], alpha=0.8)
plt.axis("equal")

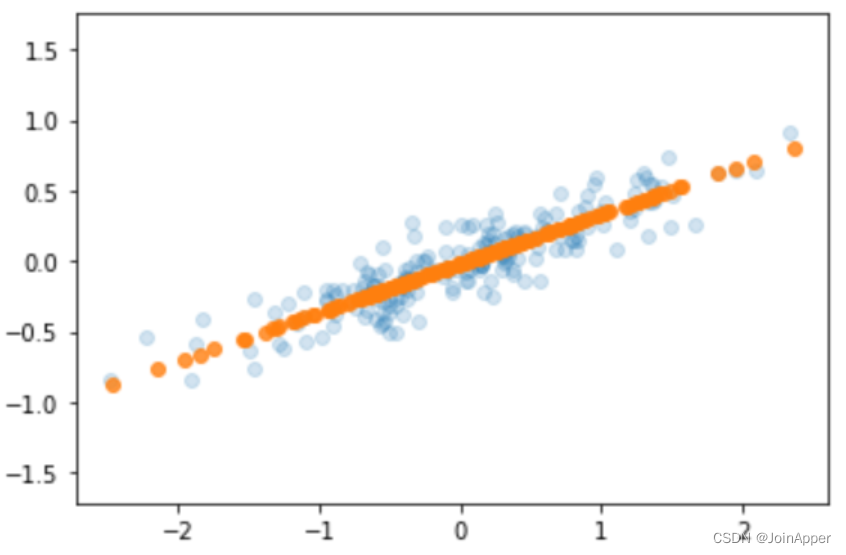
上面只是一个二维数据，确定主成分个数相对简单，但是当我们将PCA用到更高维度的数据中去的时候，应该如何确定主成分个数呢？累计方差贡献率将是一个衡量的指标。
我们可以绘制该累计曲线：

from sklearn.datasets import load_digits
# 加载手写数字数据集
digits = load_digits()
pca = PCA().fit(digits.data)
plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.xlabel("number of components")
plt.ylabel("cumulative wcplained variance")

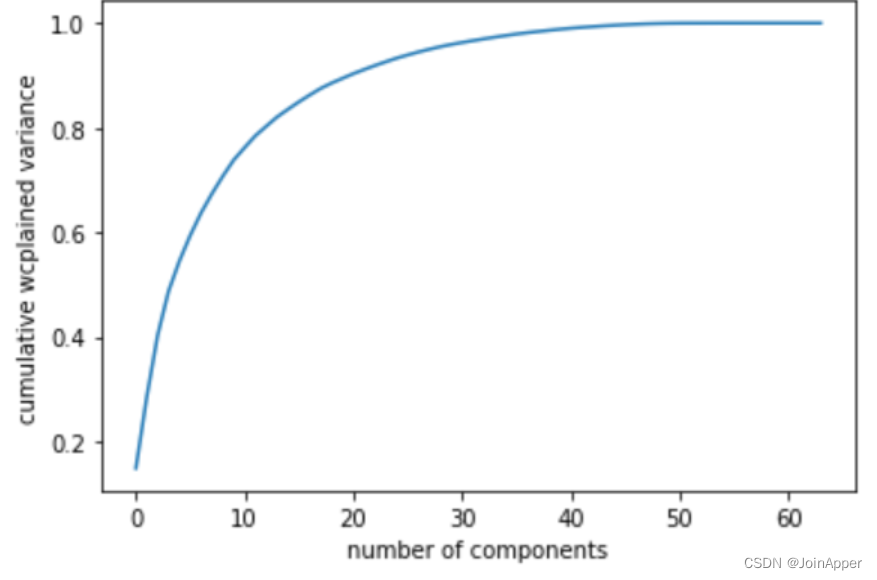
PCA噪声过滤

PCA算法经常被用做噪声数据的过滤方法，其中的原理之前也已讲过，噪声的方差小，信号的方差大。下面我们看看如何在手写数字数据中实现噪声过滤。
首先可以画出无噪声的输入数据：

def plot_digits(data):
    fig, axes = plt.subplots(4, 10, figsize=(10, 4), 
                             subplot_kw={"xticks": [], "yticks": []},
                            gridspec_kw=dict(hspace=0.1, wspace=0.1))
    for i, ax in enumerate(axes.flat):
        ax.imshow(data[i].reshape(8,8), cmap='binary', interpolation='nearest',
                 clim=(0, 16))
plot_digits(digits.data)

然后我们在原数据集上加入噪声：

np.random.seed(42)
noisy = np.random.normal(digits.data, 4)
plot_digits(noisy)

之后我们就可以使用PCA算法进行噪声过滤了：

# 保留50%的累计方差
pca = PCA(0.5).fit(noisy)
print(pca.n_components_)
components = pca.transform(noisy)
filtered = pca.inverse_transform(components)
plot_digits(filtered)

从中可以看出去噪的效果还是不错的。

总结

PCA的用途十分广泛，可以进行降维、高维数据的可视化、噪声过滤、特征选择等。但是该算法也容易被数据集中的异常点干扰，因此也产生了一些效果更好的变体PCA，比如RandomizedPCA和SparsePCA，其中RandomizedPCA使用了一个非确定方法，快速地近似计算出一个维度非常高的数据的前n个主成分，而SparsePCA则引入了一个正则项保证成分的稀疏性。

参考

《百面机器学习-算法工程师带你去面试》- 第4章降维
《Python数据科学手册》 - 第5章机器学习