主成分分析（PCA）

雷霆之王

于 2024-06-11 20:20:23 发布

阅读量1k

点赞数 15

文章标签：人工智能机器学习

本文链接：https://blog.csdn.net/m0_74739796/article/details/139607089

版权

一、PCA简介

PCA（Principal Component Analysis），即主成分分析，是一种广泛使用的数据分析方法，特别在数据降维领域。PCA的主要思想是将原始的高维特征空间通过线性变换投射到一个新的低维特征空间上，同时尽量保持原始数据的方差，使得在新的低维空间中数据的差异性得以保留。

二、计算过程（公式）

2.0 题干假设

假设我们有一个n个样本，每个样本有p个特征的数据集，记作X（n×p）。

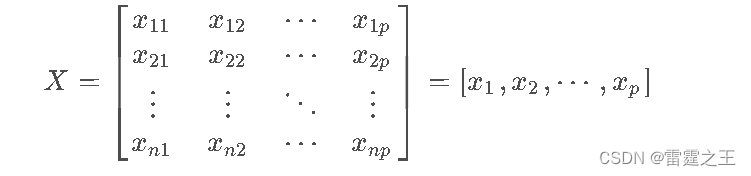
2.1 标准化

数据标准化是PCA的重要前置步骤。标准化的公式如下：
$[ Z_{ij} = \frac{X_{ij} - \mu_j}{\sigma_j} ]$
其中， $( Z_{ij} )$ 是标准化后的数据， $( X_{ij} )$ 是原始数据， $( \mu_j )$ 是第j个特征的均值， $( \sigma_j )$ 是第j个特征的标准差。

2.2 计算协方差矩阵

标准化后的数据矩阵Z的协方差矩阵C可以通过Z的转置与其自身的乘积，再除以样本数n-1得到：
$[ C = \frac{1}{n-1} Z^T Z ]$

2.3 计算特征值和特征值向量

协方差矩阵C是一个对称矩阵，可以对其进行特征值分解，得到特征值λ和对应的特征向量v。特征值分解的公式为：
$[ Cv = \lambda v ]$
其中，λ是特征值，v是对应的特征向量。

2.4 多重共线性检验

多重共线性检验是一种评估变量间是否存在高度线性关系的方法，这种关系可能会影响到模型的稳定性和解释性。在PCA中，虽然其本身就能处理多重共线性问题，但事先进行多重共线性检验有助于更好地理解数据特征之间的关系。

多重共线性的检验方法包括：

计算特征之间的相关系数矩阵：通过计算特征之间的相关系数，可以初步判断是否存在多重共线性。当相关系数接近1（或-1）时，表示两个特征之间存在高度正相关（或负相关）。
计算方差膨胀因子（VIF）：VIF是一个衡量多重共线性严重程度的指标。VIF的值越大，表示多重共线性越严重。一般来说，当VIF的值大于5或10时，认为存在多重共线性问题。

2.5 适合性检验

在进行PCA之前，进行适合性检验可以帮助我们判断数据是否适合进行主成分分析。适合性检验主要包括以下两种方法：

Kaiser-Meyer-Olkin (KMO) 检验：KMO检验用于比较变量间简单相关系数和偏相关系数的指标。KMO值越接近1，表示变量间的相关性越强，越适合进行主成分分析。一般来说，KMO值大于0.6表示适合进行PCA，而大于0.9则表示非常适合。
Bartlett's 球形检验：Bartlett's球形检验用于检验相关矩阵是否是单位矩阵，即各变量是否独立。如果检验的统计量值较大，且其对应的相伴概率值小于用户给定的显著性水平，则应该拒绝零假设，认为相关系数矩阵不可能是单位阵，即原始变量之间存在相关性，适合作主成分分析。

综上所述，通过多重共线性检验和适合性检验，我们可以更好地了解数据的特性，确保PCA的有效性。

2.6 计算主成分贡献率及累计贡献率

每个主成分的贡献率是它所对应的特征值占所有特征值之和的比例，公式为：
$[ \text{}i = \frac{\lambda_i}{\sum{j=1}^{p} \lambda_j} ]$
累计贡献率则是前k个主成分贡献率的和：

2.7 选取和表示主成分
根据累计贡献率的大小，选取前k个主成分。每个主成分都是原始变量的线性组合，公式为：
$[ F_i = a_{1i}Z_1 + a_{2i}Z_2 + \ldots + a_{pi}Z_p \quad (i = 1, 2, \ldots, k) ]$
其中， $( F_i )$ 是第i个主成分， $( a_{ji} )$ 是第j个标准化后的原始变量在第i个主成分中的系数（即特征向量v的元素）。

2.8 系数的简单分析

PCA（主成分分析）的系数简单分析，主要是对每个主成分中的系数（即特征向量的元素）进行解读，以了解每个主成分与原始变量之间的关系。以下是对PCA系数进行简单分析的步骤和要点：

理解系数的含义：
- PCA的系数，或称为特征向量中的元素，代表了原始变量在构成主成分时的权重或贡献度。
- 每个主成分都是原始变量的线性组合，系数则决定了原始变量在该主成分中的相对重要性。
分析系数的绝对值：
- 系数的绝对值大小反映了原始变量对主成分的影响程度。绝对值越大，说明该原始变量在主成分中的贡献越大。
- 通过比较不同主成分的系数绝对值，可以识别出哪些原始变量对特定主成分的影响最为显著。
分析系数的正负号：
- 系数的正负号表示了原始变量与主成分之间的正负相关性。
- 正系数表示原始变量与主成分呈正相关，即当原始变量值增加时，主成分的值也倾向于增加。
- 负系数表示原始变量与主成分呈负相关，即当原始变量值增加时，主成分的值倾向于减少。
综合分析与解读：
- 通过综合分析不同主成分的系数，可以了解每个主成分主要代表了哪些原始变量的信息。
- 例如，如果某个主成分在几个与原始数据集中特定概念或领域相关的变量上具有较大的系数，那么这个主成分可能主要反映了这些变量的综合信息。
- 另外，系数的分析也可以帮助我们理解原始变量之间的潜在关系，如哪些变量之间存在正相关或负相关关系。
具体案例（以葡萄酒数据集为例）：
- 假设我们在葡萄酒数据集中进行了PCA分析，并得到了多个主成分。
- 对于第一个主成分（通常包含最大的方差），我们可以检查其系数。如果某些与葡萄酒风味或质量相关的变量（如糖分、酸度、单宁等）具有较大的系数，那么这个主成分可能主要反映了葡萄酒的整体风味或质量。
- 对于后续的主成分，我们可以继续分析它们的系数，以了解它们分别代表了哪些方面的信息（如产地、年份等）。

三、phyon代码实现PCA

为了使用Python自主实现主成分分析（PCA）并可视化结果，遵循以下步骤：

准备数据集
标准化数据集（使得每个特征的均值为0，标准差为1）
计算协方差矩阵
计算协方差矩阵的特征值和特征向量
选择主成分（基于特征值的大小）
转换数据到新的主成分空间
可视化结果（对于二维或三维数据）

import numpy as np  
import matplotlib.pyplot as plt  
from sklearn.datasets import load_iris  # 加载鸢尾花数据集作为示例  
  
# 自主实现PCA  
def pca(X, n_components):  
    # 1. 数据标准化  
    X_mean = np.mean(X, axis=0)  
    X_std = np.std(X, axis=0)  
    X_normalized = (X - X_mean) / X_std  
  
    # 2. 计算协方差矩阵  
    covariance_matrix = np.cov(X_normalized, rowvar=False)  
  
    # 3. 计算协方差矩阵的特征值和特征向量  
    eigenvalues, eigenvectors = np.linalg.eig(covariance_matrix)  
  
    # 4. 对特征值和特征向量按大小进行排序（从大到小）  
    idx = eigenvalues.argsort()[::-1]  
    eigenvalues = eigenvalues[idx]  
    eigenvectors = eigenvectors[:, idx]  
  
    # 5. 选择主成分  
    principal_components = eigenvectors[:, :n_components]  
  
    # 6. 转换数据到新的主成分空间  
    X_pca = np.dot(X_normalized, principal_components)  
  
    return X_pca, principal_components, eigenvalues  
  
# 加载数据集（这里使用鸢尾花数据集，但只取前两个特征以便可视化）  
iris = load_iris()  
X = iris.data[:, :2]  # 只取前两个特征  
y = iris.target  
  
# 执行PCA并选择前两个主成分  
X_pca, principal_components, eigenvalues = pca(X, 2)  
  
# 可视化原始数据和PCA结果  
plt.figure(figsize=(10, 5))  
  
# 原始数据散点图  
plt.subplot(1, 2, 1)  
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis', alpha=0.7, edgecolor='k')  
plt.xlabel('Feature 1')  
plt.ylabel('Feature 2')  
plt.title('Original Data')  
  
# PCA结果散点图  
plt.subplot(1, 2, 2)  
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, cmap='viridis', alpha=0.7, edgecolor='k')  
plt.xlabel('PC 1')  
plt.ylabel('PC 2')  
plt.title('PCA Transformed Data')  
  
# 显示图形  
plt.tight_layout()  
plt.show()

3.1.实验结果图：

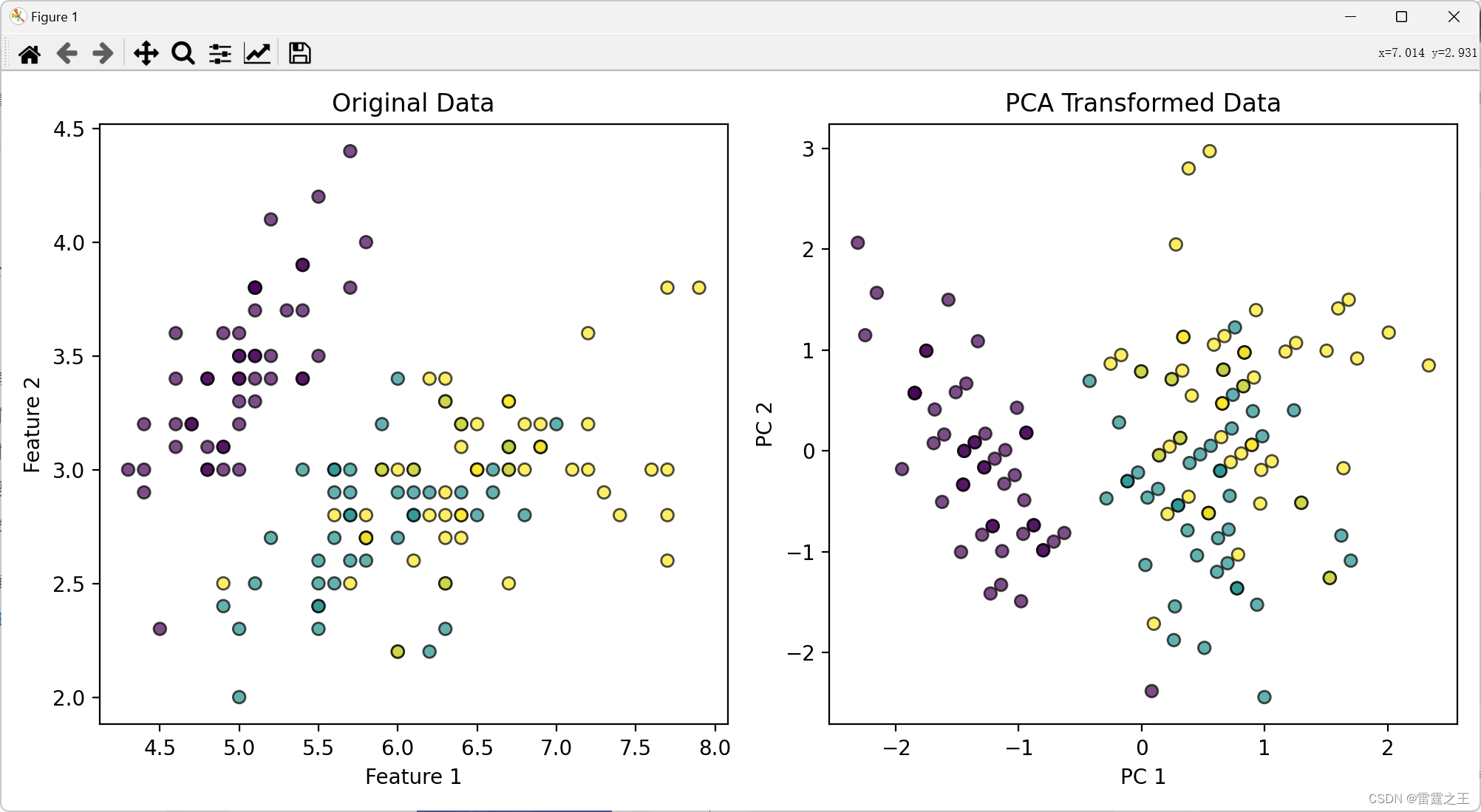
3.2.实验结果分析

数据点分布的变化：
- 在原始数据中，如果存在多个维度，数据点的分布难以在二维或三维空间中直接观察。PCA通过线性变换将数据投影到新的坐标轴上，这些坐标轴（即主成分）是按照数据方差大小排序的。
- 在降维后的散点图中，数据点沿着主成分的方向重新分布。原始数据中存在明显的聚类或线性关系，这些关系在降维后的散点图中更加明显。
主成分的选择与贡献：
- PCA通过计算协方差矩阵的特征值和特征向量来选择主成分。特征值的大小反映了对应主成分对数据方差的贡献程度。
- 选择的主成分数量决定了降维后的数据维度。选择的主成分越多，保留的原始信息就越多，但降维的效果可能不明显；选择的主成分过少，则可能丢失重要的信息。
- 在散点图中，可以观察到随着主成分数量的减少，数据点的分布变得更加紧凑或模糊，因为一些细节信息被丢弃了。
冗余信息的去除：
- PCA的一个重要应用是去除数据中的冗余信息。在降维过程中，PCA会优先保留数据中的主要变化方向（即方差最大的方向），而忽略那些方差较小的方向（往往包含噪声和冗余信息）。
- 在散点图中，这种去除冗余信息的效果表现为数据点的分布变得更加清晰和易于区分。特别是当原始数据中存在大量噪声或冗余特征时，PCA的降维效果会更加显著。

雷霆之王

关注

15
点赞
踩
33

收藏

觉得还不错? 一键收藏
1
评论
主成分分析（PCA）

PCA（Principal Component Analysis），即主成分分析，是一种广泛使用的数据分析方法，特别在数据降维领域。PCA的主要思想是将原始的高维特征空间通过线性变换投射到一个新的低维特征空间上，同时尽量保持原始数据的方差，使得在新的低维空间中数据的差异性得以保留。
复制链接

扫一扫