自然排序

自然排序

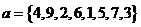
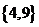
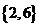
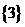
       如果数组中部分元素已按自然数顺序排放，例如，数组，则初期自然排好序的子数组段显然有4段，分别为，，和。请充分利用上述特点设计并实现一个自然合并排序算法，并分析该算法的计算时间复杂度。

【分析】

       我们先是线性扫描，将数组a中的子数组段的开始下标保存在数组b中。接着采用分治的思想，对数组b进行先“分治”后“合并”。如：对于a = {4,9,2,6,1,5,7,3}来说，b = {0,2,4,7}。对b进行分治分为{0,2}，{4,7}，再进行合并，即{4,9}和{2,6}的合并、{1,5,7}和{3}的合并。最后再将{2,4,6,9}和{1,3,5,7}合并。类似于归并排序算法。同样该算法的时间复杂度为O(n * log n)。

       我们需要注意的是，处理好原数组a与新生数组b的关系，再对b数组进行分治后，如何运用b数组的值转变为a数组的下标，以至于得出数组a的合并范围。

【程序】

用java语言编写程序，代码如下：

public class NatureSort {
	public static void main(String[] args) {
		int[] a = {4, 9, 2, 6, 1, 5, 7, 3};
		
		int[] b = new int[8];
		int len = partition(a, 8, b);
		/*for(int i = 0; i < len; i++)
			System.out.println(b[i]);*/
		
		natureSort(a, 8, b, len, 0, len - 1);
		
		System.out.print(a[0]);
		for(int i = 1; i < 8; i++)
			System.out.print(" " + a[i]);
		System.out.println();
		
		
	}
	
	public static int partition(int[] a, int n, int[] b) {
		int len = 1;
		b[0] = 0;
		for(int i = 1; i < n; i++) {
			if(a[i] < a[i - 1])
				b[len++] = i;
		}
		
		return len;
	}
	
	public static void natureSort(int[] a, int n, int[] b, int len, int left, int right) {
		if(right - left > 0) {
			int mid = (left + right) / 2;
			natureSort(a, n, b, len, left, mid);
			natureSort(a, n, b, len, mid + 1, right);
			
			int mleft, mmid, mright;
			mleft = b[left];
			mmid = b[mid + 1] - 1;
			if(right + 1 < len)
				mright = b[right + 1] - 1;
			else
				mright = n - 1;
			
			merge(a, mleft, mmid, mright);
		}
	}
	
	public static void merge(int[] a, int left, int mid, int right) {
		int c1 = left, c2 = mid + 1;
		int c = 0;
		int[] work = new int[right - left + 1];
		while(c1 <= mid && c2 <= right) {
			if(a[c1] < a[c2])
				work[c++] = a[c1++];
			else
				work[c++] = a[c2++];
		}
		
		while(c1 <= mid)
			work[c++] = a[c1++];
		
		while(c2 <= right)
			work[c++] = a[c2++];
		
		for(int i = left, j = 0; i <= right; i++, j++)
			a[i] = work[j];
	}
}

【结果】