1.K-Means算法
由于具有出色的速度和良好的可扩展性,K-Means聚类算法算得上是最著名的聚类方法。K-Means算
法是一个重复移动类中心点的过程,把类的中心点,也称重心(centroids),移动到其包含成员的平
均位置,然后重新划分其内部成员。 是算法计算出的超参数,表示类的数量;K-Means可以自动分
配样本到不同的类,但是不能决定究竟要分几个类。 必须是一个比训练集样本数小的正整数。
有时,类的数量是由问题内容指定的。也有一些问题没有指定聚类的数量,最优的聚类
数量是不确定的。后面我们会介绍一种启发式方法来估计最优聚类数量,称为肘部法则(Elbow
Method)。
K-Means的参数是类的重心位置和其内部观测值的位置。与广义线性模型和决策树类似,K-Means参
数的最优解也是以成本函数最小化为目标。K-Means成本函数公式如下:
是第 uk个类的重心位置。成本函数是各个类畸变程度(distortions)之和。每个类的畸变程度等于
该类重心与其内部成员位置距离的平方和。若类内部的成员彼此间越紧凑则类的畸变程度越小,反
之,若类内部的成员彼此间越分散则类的畸变程度越大。求解成本函数最小化的参数就是一个重复配
置每个类包含的观测值,并不断移动类重心的过程。首先,类的重心是随机确定的位置。实际上,重
心位置等于随机选择的观测值的位置。每次迭代的时候,K-Means会把观测值分配到离它们最近的
类,然后把重心移动到该类全部成员位置的平均值那里。
原始数据:
2004-01-02,17.96,18.68,17.54,18.22
2004-01-05,18.45,18.49,17.44,17.49
2004-01-06,17.66,17.67,16.19,16.73
2004-01-07,16.72,16.75,15.05,15.05
2004-01-08,15.42,15.68,15.32,15.61
2004-01-09,16.15,16.88,15.57,16.75
2004-01-12,17.32,17.46,16.79,16.82
2004-01-13,16.06,18.33,16.53,18.04
2004-01-14,17.29,17.03,16.04,16.75
2004-01-15,17.07,17.31,15.49,15.56
2004-01-16,15.04,15.44,14.09,15
2004-01-20,15.77,16.13,15.09,15.21
2004-01-21,15.63,15.63,14.24,14.34
2004-01-22,14.02,14.87,14.01,14.71
2004-01-23,14.73,15.05,14.56,14.84
2004-01-26,15.78,15.78,14.52,14.55
2004-01-27,15.28,15.44,14.74,15.35
2004-01-28,15.37,17.06,15.29,16.78
2004-01-29,16.88,17.66,16.79,17.14
2.聚类趋势
'''
Created on 2017年9月21日
@author: zawdcxs
'''
import numpy as np
#读取数据
X = []
f = open('cluster.txt')
for v in f:
X.append(
[float(v.split(',')[-2]),
float(v.split(',')[-1])])
#转换成numpy array
X 







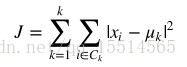
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








