Python做手写数字识别

最近在学neural networks and deeplearning这本书，也跟着做了一下实验，这本书的地址是http://neuralnetworksanddeeplearning.com/chap1.html，当然网络上也有翻译版的，可以下载看。由于刚开始学Python，难免会遇到很多错误，把这些过程记下来，便于自己以后学习和同大家交流。
我用的是Python2.7.13和https://pan.baidu.com/s/1c2pJFMC 密码: px9v 数据集，步骤就是跟着Michael Nielsen教授一步一步来的，本章是书中的第一章，利用神经网络梯度下降算法来做的，以后每学习一章，我会把心得和代码都放在上面。
首先要做的事情是配置Python环境，在这里就不多说了。下面就进入正题吧。
一：在Python的安装目录下创建network.py文件，如下图所示：

在network.py文件里输入如下代码：

"""
network.py
~~~~~~~~~~

A module to implement the stochastic gradient descent learning
algorithm for a feedforward neural network.  Gradients are calculated
using backpropagation.  Note that I have focused on making the code
simple, easily readable, and easily modifiable.  It is not optimized,
and omits many desirable features.
"""

import random


import numpy as np

class Network(object):

    def __init__(self, sizes):
        """The list ``sizes`` contains the number of neurons in the
        respective layers of the network.  For example, if the list
        was [2, 3, 1] then it would be a three-layer network, with the
        first layer containing 2 neurons, the second layer 3 neurons,
        and the third layer 1 neuron.  The biases and weights for the
        network are initialized randomly, using a Gaussian
        distribution with mean 0, and variance 1.  Note that the first
        layer is assumed to be an input layer, and by convention we
        won't set any biases for those neurons, since biases are only
        ever used in computing the outputs from later layers."""
        self.num_layers = len(sizes)
        self.sizes = sizes
        self.biases = [np.random.randn(y, 1) for y in sizes[1:]]
        self.weights = [np.random.randn(y, x)
                        for x, y in zip(sizes[:-1], sizes[1:])]

    def feedforward(self, a):
        """Return the output of the network if ``a`` is input."""
        for b, w in zip(self.biases, self.weights):
            a = sigmoid(np.dot(w, a)+b)
        return a

    def SGD(self, training_data, epochs, mini_batch_size, eta,
            test_data=None):
        """Train the neural network using mini-batch stochastic
        gradient descent.  The ``training_data`` is a list of tuples
        ``(x, y)`` representing the training inputs and the desired
        outputs.  The other non-optional parameters are
        self-explanatory.  If ``test_data`` is provided then the
        network will be evaluated against the test data after each
        epoch, and partial progress printed out.  This is useful for
        tracking progress, but slows things down substantially."""
        if test_data: n_test = len(test_data)
        n = len(training_data)
        for j in xrange(epochs):
            random.shuffle(training_data)
            mini_batches = [
                training_data[k:k+mini_batch_size]
                for k in xrange(0, n, mini_batch_size)]
            for mini_batch in mini_batches:
                self.update_mini_batch(mini_batch, eta)
            if test_data:
                print "Epoch {0}: {1} / {2}".format(
                    j, self.evaluate(test_data), n_test)
            else:
                print "Epoch {0} complete".format(j)

    def update_mini_batch(self, mini_batch, eta):
        """Update the network's weights and biases by applying
        gradient descent using backpropagation to a single mini batch.
        The ``mini_batch`` is a list of tuples ``(x, y)``, and ``eta``
        is the learning rate."""
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        for x, y in mini_batch:
            delta_nabla_b, delta_nabla_w = self.backprop(x, y)
            nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
            nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
        self.weights = [w-(eta/len(mini_batch))*nw
                        for w, nw in zip(self.weights, nabla_w)]
        self.biases = [b-(eta/len(mini_batch))*nb
                       for b, nb in zip(self.biases, nabla_b)]

    def backprop(self, x, y):
        """Return a tuple ``(nabla_b, nabla_w)`` representing the
        gradient for the cost function C_x.  ``nabla_b`` and
        ``nabla_w`` are layer-by-layer lists of numpy arrays, similar
        to ``self.biases`` and ``self.weights``."""
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        # feedforward
        activation = x
        activations = [x] # list to store all the activations, layer by layer
        zs = [] # list to store all the z vectors, layer by layer
        for b, w in zip(self.biases, self.weights):
            z = np.dot(w, activation)+b
            zs.append(z)
            activation = sigmoid(z)
            activations.append(activation)
        # backward pass
        delta = self.cost_derivative(activations[-1], y) * \
            sigmoid_prime(zs[-1])
        nabla_b[-1] = delta
        nabla_w[-1] = np.dot(delta, activations[-2].transpose())
        # Note that the variable l in the loop below is used a little
        # differently to the notation in Chapter 2 of the book.  Here,
        # l = 1 means the last layer of neurons, l = 2 is the
        # second-last layer, and so on.  It's a renumbering of the
        # scheme in the book, used here to take advantage of the fact
        # that Python can use negative indices in lists.
        for l in xrange(2, self.num_layers):
            z = zs[-l]
            sp = sigmoid_prime(z)
            delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
            nabla_b[-l] = delta
            nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
        return (nabla_b, nabla_w)

    def evaluate(self, test_data):
        """Return the number of test inputs for which the neural
        network outputs the correct result. Note that the neural
        network's output is assumed to be the index of whichever
        neuron in the final layer has the highest activation."""
        test_results = [(np.argmax(self.feedforward(x)), y)
                        for (x, y) in test_data]
        return sum(int(x == y) for (x, y) in test_results)

    def cost_derivative(self, output_activations, y):
        """Return the vector of partial derivatives \partial C_x /
        \partial a for the output activations."""
        return (output_activations-y)
    def sigmoid(z):
    """The sigmoid function."""
    return 1.0/(1.0+np.exp(-z))

    def sigmoid_prime(z):
    """Derivative of the sigmoid function."""
    return sigmoid(z)*(1-sigmoid(z))

然后保存该文件。
二：在与上述相同的目录下创建mnist_loader.py文件，如下图所示：

在该文件里写入如下代码：
“””
mnist_loader
~~~~~~~~

A library to load the MNIST image data. For details of the data
structures that are returned, see the doc strings for load_data
and load_data_wrapper. In practice, load_data_wrapper is the
function usually called by our neural network code.
“”“

import cPickle
import gzip

import numpy as np

def load_data():
“”“Return the MNIST data as a tuple containing the training data,
the validation data, and the test data.

The ``training_data`` is returned as a tuple with two entries.
The first entry contains the actual training images.  This is a
numpy ndarray with 50,000 entries.  Each entry is, in turn, a
numpy ndarray with 784 values, representing the 28 * 28 = 784
pixels in a single MNIST image.

The second entry in the ``training_data`` tuple is a numpy ndarray
containing 50,000 entries.  Those entries are just the digit
values (0...9) for the corresponding images contained in the first
entry of the tuple.

The ``validation_data`` and ``test_data`` are similar, except
each contains only 10,000 images.

This is a nice data format, but for use in neural networks it's
helpful to modify the format of the ``training_data`` a little.
That's done in the wrapper function ``load_data_wrapper()``, see
below.
"""
f = gzip.open('C:\\Python27\\mnist.pkl.gz', 'rb')
training_data, validation_data, test_data = cPickle.load(f)
f.close()
return (training_data, validation_data, test_data)

def load_data_wrapper():
“”“Return a tuple containing (training_data, validation_data,
test_data). Based on load_data, but the format is more
convenient for use in our implementation of neural networks.

In particular, ``training_data`` is a list containing 50,000
2-tuples ``(x, y)``.  ``x`` is a 784-dimensional numpy.ndarray
containing the input image.  ``y`` is a 10-dimensional
numpy.ndarray representing the unit vector corresponding to the
correct digit for ``x``.

``validation_data`` and ``test_data`` are lists containing 10,000
2-tuples ``(x, y)``.  In each case, ``x`` is a 784-dimensional
numpy.ndarry containing the input image, and ``y`` is the
corresponding classification, i.e., the digit values (integers)
corresponding to ``x``.

Obviously, this means we're using slightly different formats for
the training data and the validation / test data.  These formats
turn out to be the most convenient for use in our neural network
code."""
tr_d, va_d, te_d = load_data()
training_inputs = [np.reshape(x, (784, 1)) for x in tr_d[0]]
training_results = [vectorized_result(y) for y in tr_d[1]]
training_data = zip(training_inputs, training_results)
validation_inputs = [np.reshape(x, (784, 1)) for x in va_d[0]]
validation_data = zip(validation_inputs, va_d[1])
test_inputs = [np.reshape(x, (784, 1)) for x in te_d[0]]
test_data = zip(test_inputs, te_d[1])
return (training_data, validation_data, test_data)

def vectorized_result(j):
“”“Return a 10-dimensional unit vector with a 1.0 in the jth
position and zeroes elsewhere. This is used to convert a digit
(0…9) into a corresponding desired output from the neural
network.”“”
e = np.zeros((10, 1))
e[j] = 1.0
return e
然后保存该文件。
三：打开Python的IDLE：

在开始菜单下可以找到:

在里面依次输入如下信息：

import mnist_loader
training_data, validation_data, test_data = \
mnist_loader.load_data_wrapper()
import network
net = network.Network([784, 30, 10])
net.SGD(training_data, 30, 10, 3.0, test_data=test_data)
就可以得到测试结果如下图所示（可能需要等几分钟）：

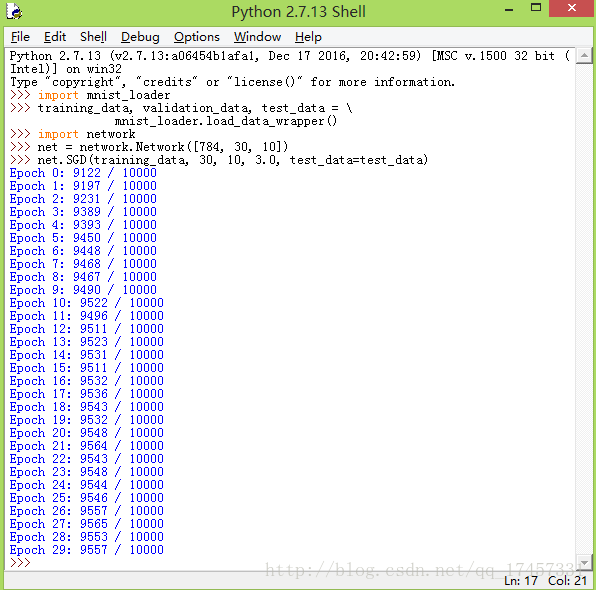
当然也可以选择不同参数来做实验，得到的结果也会是不同的。最后选择一个最合适的参数就可以了。