Leetcode 218：天际线问题（超详细的解法！！！）

城市的天际线是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。现在，假设您获得了城市风光照片（图A）上显示的所有建筑物的位置和高度，请编写一个程序以输出由这些建筑物形成的天际线（图B）。

每个建筑物的几何信息用三元组[Li，Ri，Hi]表示，其中Li和Ri分别是第 i 座建筑物左右边缘的 x 坐标，Hi 是其高度。可以保证0 ≤ Li, Ri ≤ INT_MAX, 0 < Hi ≤ INT_MAX和Ri - Li > 0。您可以假设所有建筑物都是在绝对平坦且高度为 0 的表面上的完美矩形。

例如，图A中所有建筑物的尺寸记录为：[[2 9 10], [3 7 15], [5 12 12], [15 20 10], [19 24 8]]。

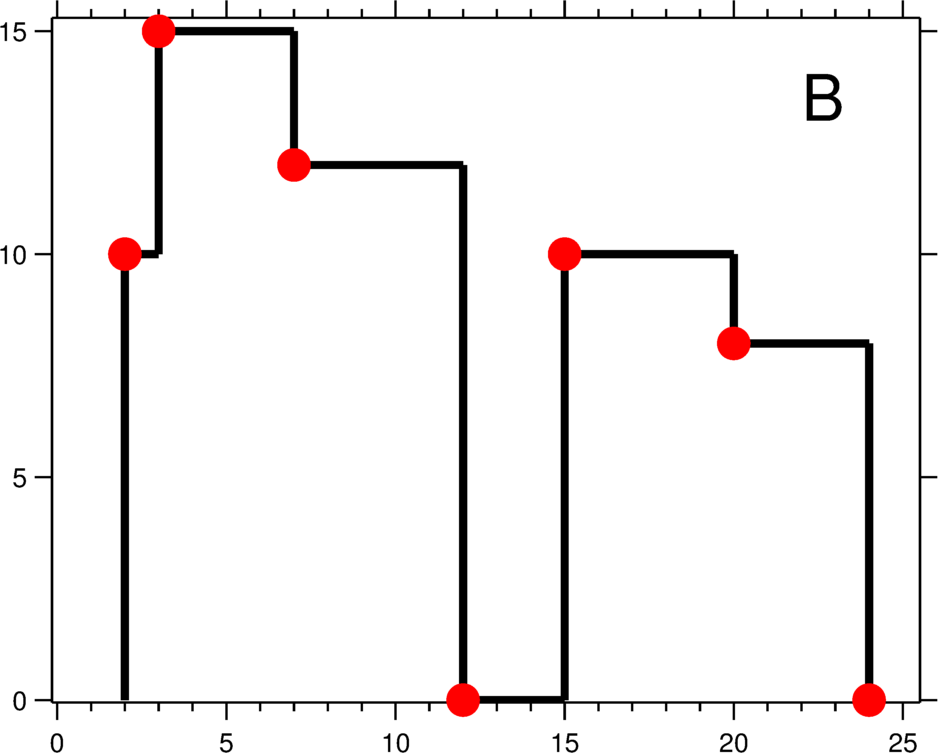
输出是以 [[x1,y1], [x2, y2], [x3, y3], ... ] 格式的“关键点”（图B中的红点）的列表，它们唯一地定义了天际线。关键点是水平线段的左端点。请注意，最右侧建筑物的最后一个关键点仅用于标记天际线的终点，并始终为零高度。此外，任何两个相邻建筑物之间的地面都应被视为天际线轮廓的一部分。

例如，图B中的天际线应该表示为：[[2 10], [3 15], [7 12], [12 0], [15 10], [20 8], [24, 0]]。

说明:

• 任何输入列表中的建筑物数量保证在[0, 10000]范围内。
• 输入列表已经按左x坐标Li进行升序排列。
• 输出列表必须按x位排序。
• 输出天际线中不得有连续的相同高度的水平线。例如[...[2 3], [4 5], [7 5], [11 5], [12 7]...]是不正确的答案；三条高度为 5 的线应该在最终输出中合并为一个：[...[2 3], [4 5], [12 7], ...]

解题思路

观察示例不难发现关键点是高度发生变化的第一个点，所以我们可以通过扫描线法来解这个问题。我们首先需要建立一个最小堆，最小堆中维护当前位置最大高度，如果当前的最大高度发生变化就将其加入结果即可。

我们需要关注高度，所以一定会有Hi（从大到小的顺序排序），同时我们希望按照Li的大小（从小到大）排序，所以我们存放的结构就是[Li,-Hi,Ri]；还需要考虑最后一个关键点的问题，最后一个关键点高度是0，并且按照Ri从小到大排序，此时我们存放的结构就是[Ri,0,0]（将右端点高度看成是0非常关键）。我们将上面的结构进行排序得到一个关键点的集合。

现在思考遍历集合的过程中会出现的问题。如图所示：

首先，如果高度不是0的话，我们需要将[Hi, Ri]（通过Hi确定最大高度，通过Ri确定最大高度的有效位置）加入到最小堆中，以维护当前位置的最大高度。如果最大高度的右端点已经超过了当前遍历的位置，说明当前最大高度失效，所以将其弹出。如果高度出现变化，那么我们将变化的高度添加到结果中，此时结果中添加的是[Li,-Hi]。最后代码非常简洁：

import heapq
class Solution:
    def getSkyline(self, buildings: List[List[int]]) -> List[List[int]]:
        points = [(L, -H, R) for L, R, H in buildings] + [(R