Leetcode 1340：跳跃游戏V（超详细的解法！！！）

最新推荐文章于 2025-02-26 13:27:34 发布

coordinate_blog

最新推荐文章于 2025-02-26 13:27:34 发布

阅读量682

点赞数

分类专栏： leetcode解题指南 Problems 文章标签： leetcode

本文链接：https://blog.csdn.net/qq_17550379/article/details/104169328

版权

Problems 同时被 2 个专栏收录

699 篇文章

订阅专栏

leetcode解题指南

654 篇文章

订阅专栏

这道题目要求你在给定的整数数组中，根据特定的跳跃规则计算最多能访问多少个下标。可以使用记忆化搜索或贪心策略（配合单调栈）来解决。文章提供了详细的解题思路，并给出了Python解决方案。还包含了问题的链接和GitHub上的相关代码。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

给你一个整数数组 arr 和一个整数 d 。每一步你可以从下标 i 跳到：

i + x ，其中 i + x < arr.length 且 0 < x <= d 。
i - x ，其中 i - x >= 0 且 0 < x <= d 。

除此以外，你从下标 i 跳到下标 j 需要满足：arr[i] > arr[j] 且 arr[i] > arr[k] ，其中下标 k 是所有 i 到 j 之间的数字（更正式的，min(i, j) < k < max(i, j)）。

你可以选择数组的任意下标开始跳跃。请你返回你最多可以访问多少个下标。

请注意，任何时刻你都不能跳到数组的外面。

示例 1：

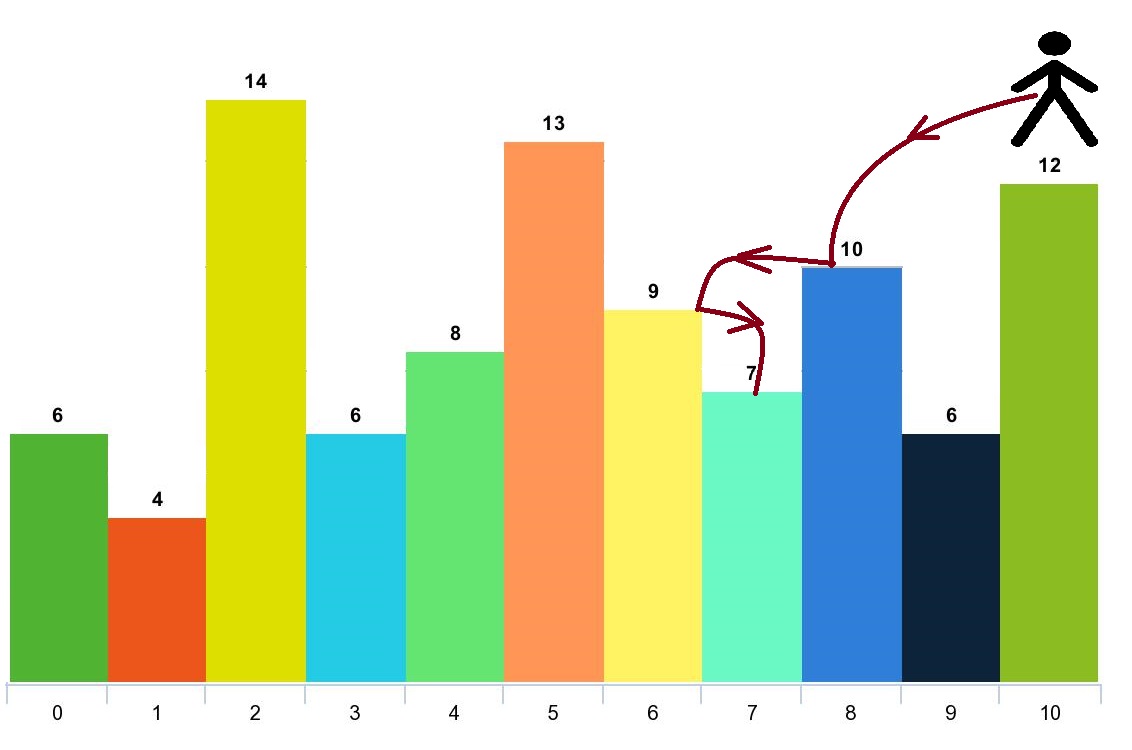
输入：arr = [6,4,14,6,8,13,9,7,10,6,12], d = 2
输出：4
解释：你可以从下标 10 出发，然后如上图依次经过 10 --> 8 --> 6 --> 7 。
注意，如果你从下标 6 开始，你只能跳到下标 7 处。你不能跳到下标 5 处因为 13 > 9 。你也不能跳到下标 4 处，因为下标 5 在下标 4 和 6 之间且 13 > 9 。
类似的，你不能从下标 3 处跳到下标 2 或者下标 1 处。

示例 2：

输入：arr = [3,3,3,3,3], d = 3
输出：1
解释：你可以从任意下标处开始且你永远无法跳到任何其他坐标。

示例 3：

输入：arr = [7,6,5,4,3,2,1], d = 1
输出：7
解释：从下标 0 处开始，你可以按照数值从大到小，访问所有的下标。

示例 4：

输入：arr = [7,1,7,1,7,1], d = 2
输出：2

示例 5：

输入：arr = [66], d = 1
输出：1

提示：

1 <= arr.length <= 1000
1 <= arr[i] <= 10^5
1 <= d <= arr.length

解题思路

比较容易想到记忆化搜索的方法来解，可以定义函数 $f (u)$ 表示从 $u\in [0,n)$ 开始跳的最多步数。那么

$f(u)=max_{i=u+1}^{u+d}f(i)+1$

需要注意的是，其中 $\leq i <n$ 并且 $a r r [u + 1] . . a r r [i] < a r r [u]$ 。另外，相反方向同理。

from functools import lru_cache
class Solution:
    def maxJumps(self, arr: List[int], d: int) -> int:
        n = len(arr)
        
        @lru_cache(None)
        def dfs(u):
            res = 1
            for k in [-1, 1]:
                for i in range(u + k, u + (d + 1) * k, k):
                    if not (0 <= i < n and arr[i] < arr[u]):
                        break
                    res = max(res, dfs(i) + 1)
            return res
        return max(map(dfs, range(n)))

如果我们反过来思考，也就是从低处向高处跳，这样就可以采用贪心的策略，每次跳最近的大于当前位置的地方。而最近的大于当前位置的地方，可以通过单调栈来求解。

from functools import lru_cache
class Solution:
    def maxJumps(self, arr: List[int], d: int) -> int:
        n = len(arr)
        s, lb, rb = [], [-1] * n, [-1] * n
        for i, v in enumerate(arr):
            while s and s[0] < i - d:
                s.pop(0)
            while s and arr[s[-1]] <= v:
                s.pop()
            if s:
                lb[i] = s[-1]
            s.append(i)
        
        s = []
        for i, v in enumerate(arr):
            while s and s[0] < i - d:
                s.pop(0)
            while s and arr[s[-1]] < v:
                rb[s.pop()] = i
            s.append(i)
        
        @lru_cache(None)
        def dfs(u):
            res = 1
            if lb[u] >= 0:
                res = max(res, dfs(lb[u]) + 1)
            if rb[u] >= 0:
                res = max(res, dfs(rb[u]) + 1)
            return res
        return max(map(dfs, range(n)))

由于我们采用贪心策略（从低向高跳），所以我们通过动态规划来解这个问题的时候，需要先对arr排序。

class Solution:
    def maxJumps(self, arr: List[int], d: int) -> int:
        n = len(arr)
        def findBigger(nums):
            s, res = [], [-1] * n
            for i, v in enumerate(nums):
                while s and s[0] < i - d:
                    s.pop(0)
                while s and nums[s[-1]] < v:
                    res[s.pop()] = i
                s.append(i)
            return res
        
        rb = findBigger(arr)
        lb = [n - i - 1 if i != -1 else -1 for i in findBigger(arr[::-1])[::-1]]
        
        dp, res = [1] * n, 0
        for _, i in sorted([v, i] for i, v in enumerate(arr))[::-1]:
            if lb[i] >= 0:
                dp[i] = max(dp[i], dp[lb[i]] + 1)
            if rb[i] >= 0:
                dp[i] = max(dp[i], dp[rb[i]] + 1)
            res = max(res, dp[i])
        return res