Leetcode 127：单词接龙（最详细的解法！！！）

最新推荐文章于 2025-03-08 21:12:16 发布

coordinate_blog

最新推荐文章于 2025-03-08 21:12:16 发布

阅读量1.5w

点赞数 1

分类专栏： Problems leetcode解题指南文章标签： leetcode

本文链接：https://blog.csdn.net/qq_17550379/article/details/83652490

版权

Problems 同时被 2 个专栏收录

699 篇文章

订阅专栏

leetcode解题指南

654 篇文章

订阅专栏

给定两个单词（beginWord 和 endWord）和一个字典，找到从 beginWord 到 endWord 的最短转换序列的长度。转换需遵循如下规则：

每次转换只能改变一个字母。
转换过程中的中间单词必须是字典中的单词。

说明:

如果不存在这样的转换序列，返回 0。
所有单词具有相同的长度。
所有单词只由小写字母组成。
字典中不存在重复的单词。
你可以假设 beginWord 和 endWord 是非空的，且二者不相同。

示例 1:

输入:
beginWord = "hit",
endWord = "cog",
wordList = ["hot","dot","dog","lot","log","cog"]
输出: 5
解释: 一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog",
     返回它的长度 5。

示例 2:

输入:
beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]
输出: 0
解释: endWord "cog" 不在字典中，所以无法进行转换。

解题思路

很明显这是一个图的问题。对于示例1来说

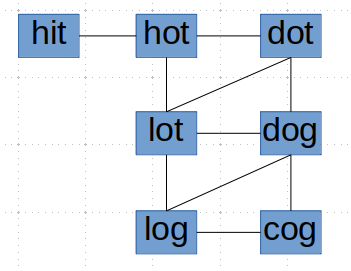
由于是求最短路径，我们很容易想到通过广度优先遍历来解决这个问题。现在我们要解决的问题就变成了如何判断两个单词只有一个字母不同。最简的办法就是通过26个字母替换

class Solution:
    def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:
        wordDict = set(wordList)
        if endWord not in wordDict:
            return 0
        
        q, visited = [(beginWord, 1)], set()
        while q:
            word, step = q.pop(0)
            if word not in visited:
                visited.add(word)
                if word == endWord:
                    return step
                for i in range(len(word)):
                    for j in 'abcdefghijklmnopqrstuvwxyz':
                        tmp = word[:i] + j + word[i+1:]
                        if tmp in wordDict and tmp not in visited: # difference
                            q.append((tmp, step + 1))

        return 0

上面的写法和传统的bfs也一点不同，不同点我在代码中已经标出出来了。我们这里对于每个tmp也判断了一次是不是在visited中，而真正的bfs算法不用这么做，这么做是为了效率。例如：

beginWord = "hit",
endWord = "cog",
wordList = ["hot","dot","dog","lot","log","cog"]

两组解：[
  ["hit","hot","dot","dog","cog"],
  ["hit","hot","lot","log","cog"]
]

如果采用了上述写法的话，只会产生一组解，问题在"hot"处就把另一组解屏蔽了。

但是这显然不是最好的做法，我们这里并不是要将单词中的每个字母用26个字母替换一遍，而是只要用特殊字符替换即可。例如hot

_ot  h_t  ho_

只会出现上述三种情况。所以我们对给定的输入hit也做相同的替换

_it  h_t  hi_

我们看hit的替换是不是出现在dict中，如果是的话，说明hit->hot是可行的，我们要判断这个路径之前有没有访问过，如果没访问过的话，我们将h_t加入q，同时我们要更新我们的step。

class Solution:
    def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:
        wordDict = collections.defaultdict(list)
        for word in wordList:
            for i in range(len(word)):
                tmp = word[:i] + "_" + word[i+1:]
                wordDict[tmp].append(word)
        
        q, visited = [(beginWord, 1)], set()
        while q:
            word, step = q.pop(0)
            if word not in visited:
                visited.add(word)
                if word == endWord:
                    return step
                for i in range(len(word)):
                    tmp = word[:i] + "_" + word[i+1:]
                    for neigh in wordDict[tmp]:
                        q.append((neigh, step + 1))
        return 0

这里我们也可以使用双向广度优先搜索。关于双向广度优先搜索其实非常简单，我们传统的广度优先搜索是从start->end，而双向的是start-><-end。我们首先建立一个stack用来存储每次访问的元素，然后先从start开始

start: hit
end: cog
wordDict: hot dot dog lot log 
stack:

我们首先将start中的每个元素从wordDict中移除。然后将start中的每个元素的每个位置替换为26个字母，然后判断替换后的单词tmp是不是在wordDict中，如果不在就继续替换，如果在的话，我们就判断tmp在不在end中，如果在的话，我们返回step+1即可，如果不在，我们将tmp加入到stack中。

start: hit
end: cog
wordDict: hot dot dog lot log 
stack: hot

然后我们判断stack.size() < end.size()，如果是的话，我们将start替换为stack，不是的话，我们将start替换为end并且将end替换为stack。同时我们要将step+1

start: cog
end: hot
wordDict: hot dot dog lot log 
stack: hot

现在我们就相当于cog->hot寻找最短路径，也就是开始从后向前查找。重复上述操作直到start和end都是空，此时我们应该返回0（因为找不到路径）。关键点在于start和end的交换，也就是判断stack.size() < end.size()。这一步主要含义就是判断start和end谁的下一步可选范围更小，我们希望从可选范围小的那一方开始搜索。

class Solution:
    def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:
        wordDict, step = set(wordList), 1
        if endWord not in wordDict:
            return 0

        s1, s2 = set([beginWord]), set([endWord])
        while s1:
            stack = set([])
            wordDict -= s1

            for s in s1:
                for i in range(len(beginWord)):
                    for j in string.ascii_lowercase:
                        tmp = s[:i] + j + s[i+1:]
                        if tmp not in wordDict:
                            continue
                        if tmp in s2:
                            return step + 1
                        stack.add(tmp)

            if len(stack) < len(s2):
                s1 = stack
            else:
                s1, s2 = s2, stack
            step += 1
        return 0