目标:已知算术掩码A、r,欲求布尔掩码x',满足
参考文献
[1] Coron J S ,Johann Großschädl, Tibouchi M ,et al.Conversion from Arithmetic to Boolean Masking with Logarithmic Complexity[C]//International Workshop on Fast Software Encryption.Springer, Berlin, Heidelberg, 2015.DOI:10.1007/978-3-662-48116-5_7.
解决方案:
1. The Ripple-Carry Adder
算法思想
其中, 是加法进位串,A、r均为k比特的数据。
令

分别对应A、r、进位串,它们之间的关系为:
![]()
即,

的获取需要k-1次迭代,由此算法的时间复杂度为O(k)。
2. The Kogge-Stone Carry Look-Ahead Adder
算法思想
类似于The Ripple-Carry Adder,其关键在于加法进位串的求取,区别在于此处加法进位串的表达由一个函数模型反复推演引申而来,而非上文的直接推导。其优势为O(log k)的时间复杂度。
推演过程具有一定的复杂性,为了方便记忆,将其摘抄于此:
此处,用c表示进位加法串,关于x+y,
令
![]()
则存在如下关系:

若i从1开始,上述关系可表示为:
单个比特之间的等同于模2乘法,单个比特间的异或等同于模2加法,
因此,上述关系又可以表示为:
该式的另一种表达方式为Q(m,0),即 其中

且 函数Q(m,n)具有如下性质:

由此可知,Q(m,0)的计算规模在每一次递归中都可以折半,通过并行,其时间复杂度可以达到对数级别.
如何在不并行的情况下,也能达到对数时间复杂度呢?
[1]作者巧思妙想,作出如下定义:

可知,.
由有:

和

且:
此时,单比特的进位表示只是换了一种递归表达方式,从Q(j,0)到G(i,j),并未看出明显的进步。
[1]作者再次定义如下变量:
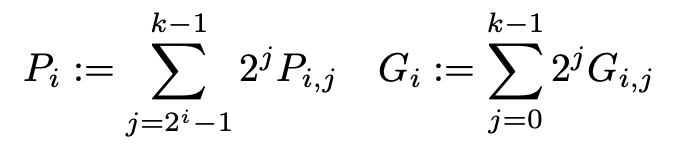
促成从单个比特的进位表示向比特串的进位表示的推进。
由于:


和

相较于之前Q(j,0)和G(i,j)的表达,Gi的计算无需在并行的环境下就能实现对数时间复杂度的计算。
此外,令
则

由于Pi和Gi的初始值分别为:

和

可得如下伪代码:

补充:
关于Q(m,n),原文的描述如下:


遗留问题:
作者怎么想到从Q(m,n) -> Pi,j & Gi,j -> Pi & Gi 这样的变化呢?























 1613
1613

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








