7-11 铁子哥采七色花 - 快速求解 S[n]=Σ(i=1~n)i^i % 7

既然网上没有原题那么这里就直接给出具体问题。

给定T组询问，每组询问输入一个整数n（1<=n<=1e9），输出S[n]的值。

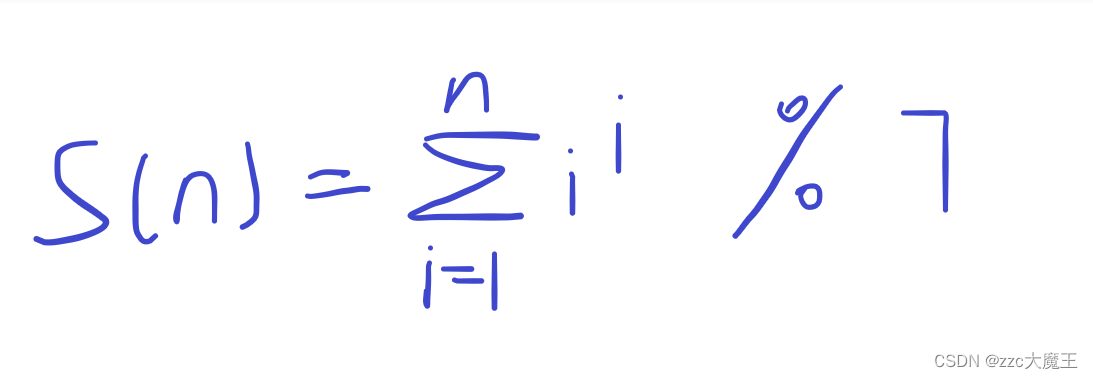
题目也没给T的范围，只是说了是一个正整数，真的很难让人分析出到底用什么方法来解决这道题。

那么做一手默认，对原式子化简

很明显就有一个递推式了，(n%7)^n不能直接用pow(n%7,n)来解决，会爆精度。

所以考虑采用快速幂中间一直取模来算出结果。

提交得到50%的分数，结果是运行超时，是快速幂的指数n太大了？

欧拉降幂+快速幂 照样只有50%的分数，因为这里模数只有7，所以phi很容易算出来是6。

底数解决了，指数解决了，理论上O（1）就把一个数算出来了，然而还是超时，也许这道题就不是优化算法能做出来的？

超时剩下的问题就是询问T的次数了。

欧拉降幂都做不出来就盲猜一手答案是有规律的（之前找过一次规律，到30为止都找不到规律）

输出了S[1]~S[500]看了一下数据，发现是有规律的...从第295个开始就是循环了。

AC代码

#include <bits/stdc++.h>
using namespace std;

string color[8]={"-1","Red","Orange","Yellow","Green","Blue","Indigo","Purple"};
int T,n,Sn;
int fuckyou[295]={0,1,5,4,1,4,5,5,6,7,4,6,7,6,6,7,2,7,1,6,7,7,1,5,6,3,7,6,6,7,1,4,6,5,6,6,7,2,4,5,7,6,6,7,4,3,7,3,4,4,5,6,3,5,6,5,5,6,1,6,7,5,6,6,7,4,5,2,6,5,5,6,7,3,5,4,5,5,6,1,3,4,6,5,5,6,3,2,6,2,3,3,4,5,2,4,5,4,4,5,7,5,6,4,5,5,6,3,4,1,5,4,4,5,6,2,4,3,4,4,5,7,2,3,5,4,4,5,2,1,5,1,2,2,3,4,1,3,4,3,3,4,6,4,5,3,4,4,5,2,3,7,4,3,3,4,5,1,3,2,3,3,4,6,1,2,4,3,3,4,1,7,4,7,1,1,2,3,7,2,3,2,2,3,5,3,4,2,3,3,4,1,2,6,3,2,2,3,4,7,2,1,2,2,3,5,7,1,3,2,2,3,7,6,3,6,7,7,1,2,6,1,2,1,1,2,4,2,3,1,2,2,3,7,1,5,2,1,1,2,3,6,1,7,1,1,2,4,6,7,2,1,1,2,6,5,2,5,6,6,7,1,5,7,1,7,7,1,3,1,2,7,1,1,2,6,7,4,1,7,7,1,2,5,7,6,7,7,1,3,5,6,1,7,7};

int main(){
    scanf("%d",&T);
    while(T--){
        scanf("%d",&n);
        cout<<color[fuckyou[(n-1)%294+1]]<<endl;
    }
    return 0;
}