区间DP入门——石子合并问题

石子合并问题是最经典的DP问题。首先它有如下3种题型：

(1)有N堆石子，现要将石子有序的合并成一堆，规定如下：每次只能移动任意的2堆石子合并，合并花费为新合成的一堆石子的数量。求将这N堆石子合并成一堆的总花费最小（或最大）。

分析：当然这种情况是最简单的情况，合并的是任意两堆，直接贪心即可，每次选择最小的两堆合并。本问题实际上就是哈夫曼的变形。

(2)有N堆石子，现要将石子有序的合并成一堆，规定如下：每次只能移动相邻的2堆石子合并，合并花费为新合成的一堆石子的数量。求将这N堆石子合并成一堆的总花费最小（或最大）。

 

分析：我们熟悉矩阵连乘，知道矩阵连乘也是每次合并相邻的两个矩阵，那么石子合并可以用矩阵连乘的方式来解决。

设dp[i][j]表示第i到第j堆石子合并的最优值，sum[i][j]表示第i到第j堆石子的总数量。那么就有状态转移公式：

[cpp]  view plain  copy

 

1. #include <iostream>  
2. #include <string.h>  
3. #include <stdio.h>  
4.   
5. using namespace std;  
6. const int INF = 1 << 30;  
7. const int N = 205;  
8.   
9. int dp[N][N];  
10. int sum[N];  
11. int a[N];  
12.   
13. int getMinval(int a[],int n)  
14. {  
15.     for(int i=0;i<n;i++)  
16.         dp[i][i] = 0;  
17.     for(int v=1;v<n;v++)  
18.     {  
19.         for(int i=0;i<n-v;i++)  
20.         {  
21.             int j = i + v;  
22.             dp[i][j] = INF;  
23.             int tmp = sum[j] - (i > 0 ? sum[i-1]:0);  
24.             for(int k=i;k<j;k++)  
25.                 dp[i][j] = min(dp[i][j],dp[i][k]+dp[k+1][j] + tmp);  
26.         }  
27.     }  
28.     return dp[0][n-1];  
29. }  
30.   
31. int main()  
32. {  
33.     int n;  
34.     while(scanf("%d",&n)!=EOF)  
35.     {  
36.         for(int i=0;i<n;i++)  
37.             scanf("%d",&a[i]);  
38.         sum[0] = a[0];  
39.         for(int i=1;i<n;i++)  
40.             sum[i] = sum[i-1] + a[i];  
41.         printf("%d\n",getMinval(a,n));  
42.     }  
43.     return 0;  
44. }  

直线取石子问题的平行四边形优化：

[cpp]  view plain  copy

 

1. #include <iostream>  
2. #include <string.h>  
3. #include <stdio.h>  
4.   
5. using namespace std;  
6. const int INF = 1 << 30;  
7. const int N = 1005;  
8.   
9. int dp[N][N];  
10. int p[N][N];  
11. int sum[N];  
12. int n;  
13.   
14. int getMinval()  
15. {  
16.     for(int i=1; i<=n; i++)  
17.     {  
18.         dp[i][i] = 0;  
19.         p[i][i] = i;  
20.     }  
21.     for(int len=1; len<n; len++)  
22.     {  
23.         for(int i=1; i+len<=n; i++)  
24.         {  
25.             int end = i+len;  
26.             int tmp = INF;  
27.             int k = 0;  
28.             for(int j=p[i][end-1]; j<=p[i+1][end]; j++)  
29.             {  
30.                 if(dp[i][j] + dp[j+1][end] + sum[end] - sum[i-1] < tmp)  
31.                 {  
32.                     tmp = dp[i][j] + dp[j+1][end] + sum[end] - sum[i-1];  
33.                     k = j;  
34.                 }  
35.             }  
36.             dp[i][end] = tmp;  
37.             p[i][end] = k;  
38.         }  
39.     }  
40.     return dp[1][n];  
41. }  
42.   
43. int main()  
44. {  
45.     while(scanf("%d",&n)!=EOF)  
46.     {  
47.         sum[0] = 0;  
48.         for(int i=1; i<=n; i++)  
49.         {  
50.             int val;  
51.             scanf("%d",&val);  
52.             sum[i] = sum[i-1] + val;  
53.         }  
54.         printf("%d\n",getMinval());  
55.     }  
56.     return 0;  
57. }  

(3)问题(2)的是在石子排列是直线情况下的解法，如果把石子改为环形排列，又怎么做呢？

分析：状态转移方程为：

其中有：

[cpp]  view plain  copy

 

1. #include <iostream>  
2. #include <string.h>  
3. #include <stdio.h>  
4.   
5. using namespace std;  
6. const int INF = 1 << 30;  
7. const int N = 205;  
8.   
9. int mins[N][N];  
10. int maxs[N][N];  
11. int sum[N],a[N];  
12. int minval,maxval;  
13. int n;  
14.   
15. int getsum(int i,int j)  
16. {  
17.     if(i+j >= n) return getsum(i,n-i-1) + getsum(0,(i+j)%n);  
18.     else return sum[i+j] - (i>0 ? sum[i-1]:0);  
19. }  
20.   
21. void Work(int a[],int n)  
22. {  
23.     for(int i=0;i<n;i++)  
24.         mins[i][0] = maxs[i][0] = 0;  
25.     for(int j=1;j<n;j++)  
26.     {  
27.         for(int i=0;i<n;i++)  
28.         {  
29.             mins[i][j] = INF;  
30.             maxs[i][j] = 0;  
31.             for(int k=0;k<j;k++)  
32.             {  
33.                 mins[i][j] = min(mins[i][j],mins[i][k] + mins[(i+k+1)%n][j-k-1] + getsum(i,j));  
34.                 maxs[i][j] = max(maxs[i][j],maxs[i][k] + maxs[(i+k+1)%n][j-k-1] + getsum(i,j));  
35.             }  
36.         }  
37.     }  
38.     minval = mins[0][n-1];  
39.     maxval = maxs[0][n-1];  
40.     for(int i=0;i<n;i++)  
41.     {  
42.         minval = min(minval,mins[i][n-1]);  
43.         maxval = max(maxval,maxs[i][n-1]);  
44.     }  
45. }  
46.   
47. int main()  
48. {  
49.     while(scanf("%d",&n)!=EOF)  
50.     {  
51.         for(int i=0;i<n;i++)  
52.             scanf("%d",&a[i]);  
53.         sum[0] = a[0];  
54.         for(int i=1;i<n;i++)  
55.             sum[i] = sum[i-1] + a[i];  
56.         Work(a,n);  
57.         printf("%d %d\n",minval,maxval);  
58.     }  
59.     return 0;  
60. }  

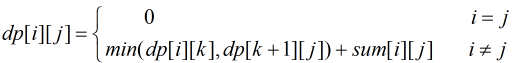
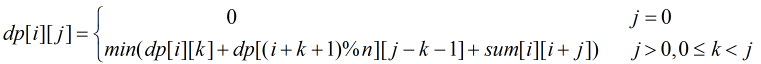
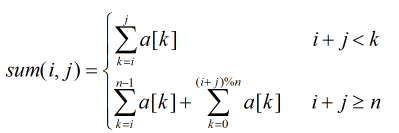
可以看出，上面的(2)(3)问题的时间复杂度都是O(n^3)，由于过程满足平行四边形法则，故可以进一步优化到O(n^2)。

对于石子合并问题，有一个最好的算法，那就是GarsiaWachs算法。时间复杂度为O(n^2)。

它的步骤如下：

设序列是stone[]，从左往右，找一个满足stone[k-1] <= stone[k+1]的k，找到后合并stone[k]和stone[k-1]，再从当前位置开始向左找最大的j，使其满足stone[j] > stone[k]+stone[k-1]，插到j的后面就行。一直重复，直到只剩下一堆石子就可以了。在这个过程中，可以假设stone[-1]和stone[n]是正无穷的。

举个例子：

186 64 35 32 103

因为35<103，所以最小的k是3，我们先把35和32删除，得到他们的和67，并向前寻找一个第一个超过67的数，把67插入到他后面，得到：186 67 64 103,现在由5个数变为4个数了，继续：186 131 103，现在k=2（别忘了，设A[-1]和A[n]等于正无穷大）234 186，最后得到420。最后的答案呢？就是各次合并的重量之和，即420+234+131+67=852。

基本思想是通过树的最优性得到一个节点间深度的约束，之后证明操作一次之后的解可以和原来的解一一对应，并保证节点移动之后他所在的深度不会改变。具体实现这个算法需要一点技巧，精髓在于不停快速寻找最小的k，即维护一个“2-递减序列”朴素的实现的时间复杂度是O(n*n)，但可以用一个平衡树来优化，使得最终复杂度为O(nlogn)。

题目：http://poj.org/problem?id=1738

[cpp]  view plain  copy

 

1. #include <iostream>  
2. #include <string.h>  
3. #include <stdio.h>  
4.   
5. using namespace std;  
6. const int N = 50005;  
7.   
8. int stone[N];  
9. int n,t,ans;  
10.   
11. void combine(int k)  
12. {  
13.     int tmp = stone[k] + stone[k-1];  
14.     ans += tmp;  
15.     for(int i=k;i<t-1;i++)  
16.         stone[i] = stone[i+1];  
17.     t--;  
18.     int j = 0;  
19.     for(j=k-1;j>0 && stone[j-1] < tmp;j--)  
20.         stone[j] = stone[j-1];  
21.     stone[j] = tmp;  
22.     while(j >= 2 && stone[j] >= stone[j-2])  
23.     {  
24.         int d = t - j;  
25.         combine(j-1);  
26.         j = t - d;  
27.     }  
28. }  
29.   
30. int main()  
31. {  
32.     while(scanf("%d",&n)!=EOF)  
33.     {  
34.         if(n == 0) break;  
35.         for(int i=0;i<n;i++)  
36.             scanf("%d",stone+i);  
37.         t = 1;  
38.         ans = 0;  
39.         for(int i=1;i<n;i++)  
40.         {  
41.             stone[t++] = stone[i];  
42.             while(t >= 3 && stone[t-3] <= stone[t-1])  
43.                 combine(t-2);  
44.         }  
45.         while(t > 1) combine(t-1);  
46.         printf("%d\n",ans);  
47.     }  
48.     return 0;  
49. }  

本人的：

/*


用T[i][j]代表从i到j连续的所有石堆合并后的整体 i<=j
dp[i][j]代表形成T[i][j]所需要的最小花费 
i==j时：
dp[i][j] = 0;因为不需要合并 因为dp数组是全局所以可以省去
i<j时：
T[i][j]肯定是由某两个【相邻】子堆组合而成 假设这个分界点是k,那么这两个子堆是T[i,k]和T[k+1][j],其中i<=k<j;
T[i][j]最小总花费是由两部分组成：
1) T[i][k]和T[k+1][j]各自的最小花费之和所形成的集合里的最小值(用k=i...j-1循环求最小和)
2) 组合T[i,k]和T[k+1][j]成为T[i][j]的动作需要的花费，其实就是这两个堆的总重量，也就是T[i][j]的重量,记录为w[i][j]
得到那么得到方程:dp[i][j] = min{dp[i][k]+dp[k+1][j]}+w[i][j];
w[i][j]一种简便求法:
我们使用w[i]来存储w[1]~w[i]所有堆重量之和
那么w[i][j]就是 w[j] - w[i-1];
自底向上构造:
注意到
所有长度为2的T[i][j]需要使用所有长度为1的T[i][j];
所有长度为3的T[i][j]需要使用所有长度为1/2的T[i][j];
所有长度为4的T[i][j]需要使用所有长度为1/2/3/4的T[i][j];
.....
所有长度为n的T[i][j]需要使用所有长度为1/2/3.....n-2/n-1的T[i][j];
用l代表长度,l->2~(n);i,j代表某一段的左右坐标
dp[i][j]代表形成T[i][j]所需要的最小花费 原问题dp[1][n]
复杂度O(n^3)
*/

#include <iostream>
#include <algorithm>
#include <climits>
using namespace std;
int w[105];
int dp[105][105];
int main()
{
int n;
cin>>n;
for(int i= 1;i<=n;i++)
{
cin>>w[i];
w[i]+=w[i-1];
}
for(int l = 2;l<=n;l++)
for(int i= 1;i<n;i++)
{
int j = i+l-1;
int amin = INT_MAX;
for(int k = i;k<j;k++)
{
amin = min(amin,dp[i][k]+dp[k+1][j]);
}
dp[i][j] = amin + w[j]-w[i-1];\
}
cout<<dp[1][n]<<endl;
}
/**
#include<iostream>
using namespace std;
int N;//石子的堆数
int num[100]={0};//每堆石子个数


int sum(int begin,int n)
{
     int total=0;
     for (int i=begin;i<=begin+n-1;i++)
     {   if(i==N)
              total=total+num[N];//取代num[0]
         else
              total=total+num[i%N];
     }
     return total;
}
int stone_merge()
{
       int score[100][100];//score[i][j]:从第i堆石子开始的j堆石子合并后最小得分
       int n,i,k,temp;
       for (i=1;i<=N;i++)
           score[i][1]=0;//一堆石子，合并得分为0


       //num[0]=num[N];//重要：sum()函数中i=N时,取num[0]
       for (n=2;n<=N;n++)//合并的石子的堆数
       {
           for (i=1;i<=N;i++)//合并起始位置
           {
               score[i][n]=score[i][1]+score[(i+1-1)%N+1][n-1];
               for (k=2;k<=n-1;k++)//截断位置
               {
                  temp=score[i][k]+score[(i+k-1)%N+1][n-k];
                  if(temp <score[i][n])
                        score[i][n] = temp;//从第i开始的k堆是：第i+0堆到第(i+k-1)%N堆
               }
               score[i][n]+=sum(i,n);
           }
       }
       int min=2147483647;
       for (i=1;i<=N;i++)
       {    if (min>score[i][N])
                  min=score[i][N];//取从第i堆开始的N堆的最小者
       }
       return min;
}


int main()
{
       int min_count=0;
       cin>>N;//石子的堆数
           for (int i=1;i<=N;i++)
               cin>>num[i];//每堆石子的数量//从1开始,num[0]不用
           min_count=stone_merge();
           cout<<min_count<<endl;
       return 0;
}
**/




#include<stdio.h>
int N;//最多100堆石子:N=100
int num[200]={0};
int max=-0x3f3f3f3f;
int stone_merge()
{
    int score[200][101]={0};//l[i][j]:从第i堆石子起合并n堆石子的最小得分
    int score2[200][101]={0};
    int n,i,k,temp,t2;
    for(i=0;i<2*N;i++)
        {
            score[i][1]=0;//一堆石子合并得分为0
            score2[i][1]=0;
        }
    for(n=2;n<=N;n++)//合并n堆石子
    {
        for(i=0;i<=2*N-n;i++)//从第i对开始合并(有一次重复运算，但省去了循环取数，简化了程序)
        {
            score[i][n]=score[i][1]+score[i+1][n-1];
            score2[i][n]=score2[i][1]+score2[i+1][n-1];
            for(k=2;k<n;k++)//划分
            {   temp=score[i][k]+score[k+i][n-k];
                t2=score2[i][k]+score2[k+i][n-k];
                if(temp<score[i][n])
                    score[i][n]=temp;//取(i,n)划分两部分的得分
                    if(t2>score2[i][n])
                        score2[i][n]=t2;
            }
            for(k=i;k<i+n;k++)
                {
                    score[i][n]+=num[k];//加上此次合并得分
                    score2[i][n]+=num[k];
                }
        }
    }
    int min=2147483647;//int(4位)最大值为2147483647
    for(i=0;i<N;i++)
    {
        if(score[i][N]<min)
            min=score[i][N];//从第i堆开始取N堆石子，的最小合并得分
            if(score2[i][N]>max)
                max=score2[i][N];
    }
    return min;
}


int main()
{
    int min_count;
    scanf("%d",&N);//N堆石子
        for(int i=0;i<N;i++)
            scanf("%d",&num[i]);//每堆石子的数量
        for(int i=N;i<2*N;i++)
            num[i]=num[i-N];//复制一倍，化简环形计算（N堆石子是围成一个环的）
        if(N==1)    min_count=0;
        else if(N==2)    min_count=num[0]+num[1];
        else    min_count=stone_merge();
        printf("%d\n",min_count);
        printf("%d\n",max);
    return 0;
}