参考文献:Needell D,VershyninR.Signal recovery from incompleteand inaccurate measurements via regularized orthogonal matching pursuit[J]. IEEEJournal on Selected Topics in Signal Processing, 2010, 4(2): 310—316.
文中符号体系:
在文中摘要部分,给出了符号体系,原始信号为 v v v,观测信号为 x x x,观测矩阵是 ϕ \phi ϕ,观测矩阵是 N N N行× d d d列,也就意味着原始信号 v v v长是 d d d,观测信号 x x x 长度是 N N N,其中 x = ϕ v + e x=\phi v+e x=ϕv+e, e e e 在此处表示误差,语言表述就是观测信号等于观测矩阵乘原始信号再加上误差。
正则化的个人理解
个人理解的正则化是一种限制条件,当我们想要拟合一条含噪曲线时,本来曲线本身阶数不高,但是由于噪声的原因,导致最终的拟合曲线将噪声也作为了拟合目标,从而出现了过拟合现象拟合了一条阶数很高的复杂曲线,这样降低了模型的适应度(不是所有信号都含有相同噪声),为了避免这种事情发生,我们引入一种限制条件,防止过拟合现象的发生,这种限制方法,称其为正则化。
正文简述部分:
主要问题与研究意义
文章中作者提出了一种正则化正交匹配追踪(ROMP)算法,该算法将贪婪算法本身速度快的优越性和正则化条件限制的高准确性相结合,最终通过最小二乘迭代解决使用不完全、不准确观测信号恢复原始数据估计值的问题。该算法理论上是基于稀疏恢复问题是等效于凸优化问题的 (也就是统一不确定性原则,个人理解此处的UUP就是RIP准则),可以将欠定性方程组的解问题转化为L1最小范数的问题。(就是在无穷多解中求解一个误差最小的解)
研究目标
该文章针对的目标是含噪信号和扰动测量中信号的恢复,在含噪信号的恢复中文中提及ROMP的算法稳定度与凸优化的稳定度相同,高于OMP算法的稳定度。
主要研究模型
ROMP算法步骤
ROMP的意思是Regularized Orthogonal Matching Pursuit 正则化正交匹配追踪算法 该算法属于贪婪算法与凸优化的结合,在原本贪婪迭代的过程加入了正则化条件。以下算法步骤中对于部分符号参数有所调整,论文中的时间较为久远,对其中一些符号采用了当下流行的压缩感知符号体系做了修改。
输入部分:观测信号的向量
y
M
×
1
y_{M\times 1}
yM×1,公共稀疏度K,传感矩阵
A
M
×
N
A_{M\times N}
AM×N。
输出部分:重构的估计稀疏向量
θ
^
1
×
N
\widehat{\theta}_{1\times N}
θ
1×N ,残差值
r
N
×
1
r_{N\times 1}
rN×1。
该算法步骤基本按照文章描述及相关博客总结,个人理解如下:
此处参考了
1、 初始化各参数,0次迭代残差
r
0
r_0
r0初始化为输入变量
y
y
y,迭代计数变量
t
t
t。
(---------------------称该步骤为算法初始化过程---------------------)
2、 计算优化问题 u 1 × N = ∣ ∣ r t − 1 , a j ∣ ∣ 2 u_{1\times N}=||r_{t-1},a_j||_2 u1×N=∣∣rt−1,aj∣∣2, j ∈ N j\in N j∈N,即将残差与传感矩阵的各列分别做内积,在 u u u中按降序排列,取前K个最大值,若 u u u 中非0值不足K个,则选取全部的非0值,并存其序号于 J J J中。
3、 在 J J J中筛选符合正则化条件的子集 J 0 J_0 J0,正则化标准意思是选择各列向量与残差内积绝对值的最大值不能比最小值大两倍以上(comparable coordinates)且能量最大的一组(with the maximal energy)。
4、 存下
J
0
J_0
J0 的序号,并入索引集中,也存下传感矩阵中
J
0
J_0
J0 的索引列,也并入索引集中。
(此处的
J
0
J_0
J0仅能保证大于等于1,这个索引集的大小会影响最终最小二乘法输出的
θ
^
\widehat{\theta}
θ
的个数,随着迭代次数的增加,这个索引集的大小会逐渐增大)
5、 利用最小二乘法求解估计值 θ ^ \widehat{\theta} θ (本次迭代中产生了几个索引列, θ ^ \widehat{\theta} θ 就比原来多了几列)
6、 更新残差 r t = y − y ^ = y − A θ ^ r_t=y-\widehat{y}=y-A\widehat{\theta} rt=y−y =y−Aθ 。此处判断残差是否满足精度要求?迭代次数 t t t 是否大于 K K K ?迭代过程中产生的索引集个数是否大于 2 K 2K 2K?三个条件满足其一停止迭代,不满足回到第2步继续迭代。
(---------------------称以上步骤为算法贪婪迭代过程过程---------------------)
7、 最终获得了K个列数索引,而原
θ
\theta
θ 是一个N长的向量,只不过是K稀疏的。所以我们按照这K个索引将最终所求得的
θ
^
\widehat{\theta}
θ
k 排好顺序填进所有的非0点中作为最终重构的稀疏向量
θ
^
\widehat{\theta}
θ
输出。
(---------------------称该步骤为算法输出最终结果---------------------)
关于正则化步骤的详细解读
(---------此处参考了博主彬彬有礼_jbb0523的流程图,对相关步骤进行了文字说明补全---------)
流程图原出处链接: 压缩感知重构算法之正则化正交匹配追踪(ROMP)_jbb0523.
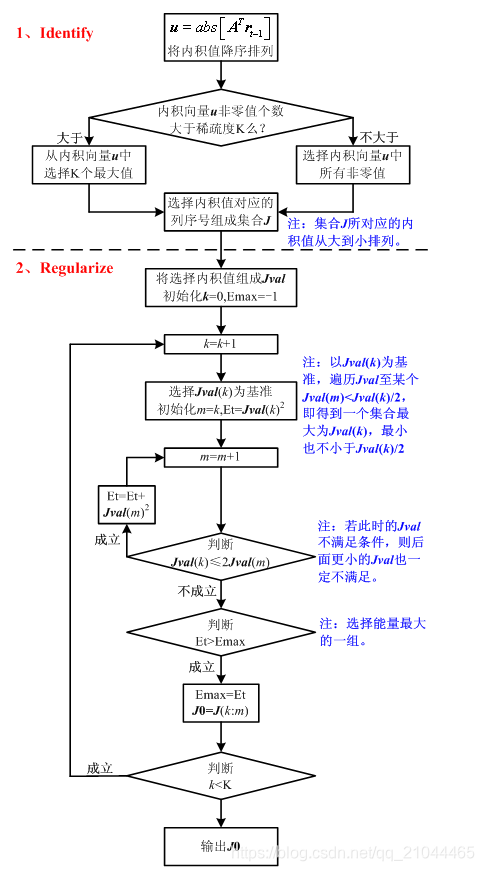
因为此处的正则化条件最开始本人阅读的时候有些问题也有点绕的云里雾里,故采用一个小例子将此处的步骤展开来看,帮助理解。
现有一个要重构的目标信号
K
=
5
K=5
K=5,初始化能量
E
t
E_t
Et
=
−
1
=-1
=−1。
经第一步计算内积,取得前7个非0值,分别是 27,26,16,15,11。
J
(
k
=
1
)
=
27
,
E
t
J(k=1)=27,E_t
J(k=1)=27,Et=
2
7
2
27^2
272
判断
2
J
(
m
=
2
)
⩾
J
(
k
=
1
)
2J(m=2) \geqslant J(k=1)
2J(m=2)⩾J(k=1) 成立,更新能量
E
t
=
2
7
2
+
2
6
2
E_t=27^2+26^2
Et=272+262。
判断
2
J
(
m
=
3
)
⩾
J
(
k
=
1
)
2J(m=3) \geqslant J(k=1)
2J(m=3)⩾J(k=1) 成立,更新能量
E
t
=
2
7
2
+
2
6
2
+
1
6
2
E_t=27^2+26^2+16^2
Et=272+262+162。
判断
2
J
(
m
=
4
)
⩾
J
(
k
=
1
)
2J(m=4) \geqslant J(k=1)
2J(m=4)⩾J(k=1) 不成立,对比该组参数的能量是否大于现有能量值,显然大于-1,故更新能量值
E
t
m
a
x
=
2
7
2
+
2
6
2
+
1
6
2
E_{tmax}=27^2+26^2+16^2
Etmax=272+262+162
判断此时
k
<
K
k<K
k<K,输出
J
0
=
J
(
k
:
m
)
,
k
=
k
+
1
J_0=J(k:m),k=k+1
J0=J(k:m),k=k+1继续迭代。
J
(
k
=
2
)
=
26
,
E
t
J(k=2)=26,E_t
J(k=2)=26,Et=
2
6
2
26^2
262
判断
2
J
(
m
=
3
)
⩾
J
(
k
=
2
)
2J(m=3) \geqslant J(k=2)
2J(m=3)⩾J(k=2) 成立,更新能量
E
t
=
2
6
2
+
1
6
2
E_t=26^2+16^2
Et=262+162。
判断
2
J
(
m
=
4
)
⩾
J
(
k
=
2
)
2J(m=4) \geqslant J(k=2)
2J(m=4)⩾J(k=2) 成立,更新能量
E
t
=
2
6
2
+
1
6
2
+
1
5
2
E_t=26^2+16^2+15^2
Et=262+162+152。
判断
2
J
(
m
=
5
)
⩾
J
(
k
=
2
)
2J(m=5) \geqslant J(k=2)
2J(m=5)⩾J(k=2) 不成立,对比该组参数的能量是否大于现有能量值,不大于,故不更新能量值,本次迭代无用。
J
(
k
=
3
)
=
16
,
E
t
J(k=3)=16,E_t
J(k=3)=16,Et=
1
6
2
16^2
162
判断
2
J
(
m
=
4
)
⩾
J
(
k
=
3
)
2J(m=4) \geqslant J(k=3)
2J(m=4)⩾J(k=3) 成立,更新能量
E
t
=
1
6
2
+
1
5
2
E_t=16^2+15^2
Et=162+152。
判断
2
J
(
m
=
5
)
⩾
J
(
k
=
3
)
2J(m=5) \geqslant J(k=3)
2J(m=5)⩾J(k=3) 成立,更新能量
E
t
=
1
6
2
+
1
5
2
+
1
1
2
E_t=16^2+15^2+11^2
Et=162+152+112。
判断
2
J
(
m
=
6
)
⩾
J
(
k
=
3
)
2J(m=6) \geqslant J(k=3)
2J(m=6)⩾J(k=3) 不成立,(
J
J
J只有5个,
J
(
6
)
=
0
J(6)=0
J(6)=0)对比该组参数的能量是否大于现有能量值,不大于,故不更新能量值,本次迭代无用。
………………
直到
J
(
k
=
5
)
=
11
,
E
t
J(k=5)=11,E_t
J(k=5)=11,Et=
1
1
2
11^2
112
判断
2
J
(
m
=
6
)
⩾
J
(
k
=
5
)
2J(m=6) \geqslant J(k=5)
2J(m=6)⩾J(k=5) 不成立,(
J
J
J只有5个,
J
(
6
)
=
0
J(6)=0
J(6)=0)对比该组参数的能量是否大于现有能量值,不大于,故不更新能量值,本次迭代无用。
该迭代过程直到最后仅输出了
J
0
=
27
,
26
,
16
J_0={27,26,16}
J0=27,26,16
将该索引集加入计算最小二乘的A向量中,并将位置序号保存至索引集中。
在进行整体最小二乘迭代,从而更新残差。
实验设置
关于实验数据,在该文章的实验设置中,测试的是ROMP的算法稳定,分别模拟了信号本身受干扰的情况和观测过程受干扰的情况。每组分别进行了500次试验。
1、 观测信号本身是采用了生成随机序列作为输入信号。
2、 在模拟信号本身干扰的时候添加了d维的高斯随机误差信号至生成的原信号v中。
3、 在模拟观测受干扰的情况时,添加N维误差向量至观测矩阵
ϕ
\phi
ϕ 中。
结论
当观测矩阵受扰动且原始信号稀疏度固定时,随观测数的增加,误差比在不断减小。
当观测矩阵受扰动且原始信号观测值固定时,随着原始信号稀疏度的增加,误差比在不断增大。

当观测信号受扰动且原始信号稀疏度固定时,随观测数的增加,误差比在不断减小。
当观测信号受扰动且原始信号观测值固定时,随着原始信号稀疏度的增加,误差比在不断增大。

图截取自论文第四节后半部分,正文Page_12
总结
ROMP算法的原始提出文献中研究目标是提高算法稳定度,这就与OMP中的以重构精度为目的有本质不同,之前光看 博主彬彬有礼_jbb0523 的博客始终有一个疑问就是为什么ROMP算法的重构效果不如OMP,甚至不太好,还成为了一个较为有代表性的算法。
将来在对压缩感知重构算法的研究上确实不能只针对于重构精确度、重构所需最小观测值、重构时间等常规参数,还要想到类似于特殊特征信号重构以及重构算法适应度、稳定度等问题。
























 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








