最小度限制生成树

设G=(V, E, ω)是连通的无向图，v0 ∈V是特别指定的一个顶点,k为给定的一个正整数。如果T是G的一个生成树且dT(v0)=k，则称T为G的k度限制生成树。G中权值和最小的k度限制生成树称为G的最小k度限制生成树

明确几个概念
T为图G的一个生成树，T+a-b记作(+a,-b)，如果T+a-b仍然是一个生成树，则称(+a,-b）是T的一个可行交换。

T为图G的一个生成树，由T进行一次可行交换得到的新的生成树所组成的集合，称为T的邻集,记为N(T)。

定 理

定理：设T是图G的最小k度限制树，E0是G中与v0有关联的边的集合，
E1=E0\E(T)，
E1即是和V0相连，但是不在T中的边的集合
E2=E(T)\E0，
E2即是T中不和V0相连的边的集合
A={(+a,-b)| a∈E1,b∈E2}
设ω(a’)－ω(b’)=min{ω(a)－ω(b)| (+a,-b)∈A}，则T + a’-b’是G的一个最小k+1度限制生成树。

即最小k+1度限制生成树属于最小k度限制生成树的邻集。

---

假设我们已经得到了最小p度限制生成树，
如何通过它来求最小p+1度限制生成树呢？

由定理可知最小p+1度限制生成树属于最小p度生成树的邻集，因此它可以通过枚举最小p度生成树上的一次可行交换求得。

为了使v0的度增加，枚举的可行交换中必须有一条边与v0关联。

如图，假设我们已经得到了v0点度为2时的最小生成树，现在要求v0度为3时的最小生成树。

我们枚举于V0关联且不在树上边，分别添加到树上，例如：

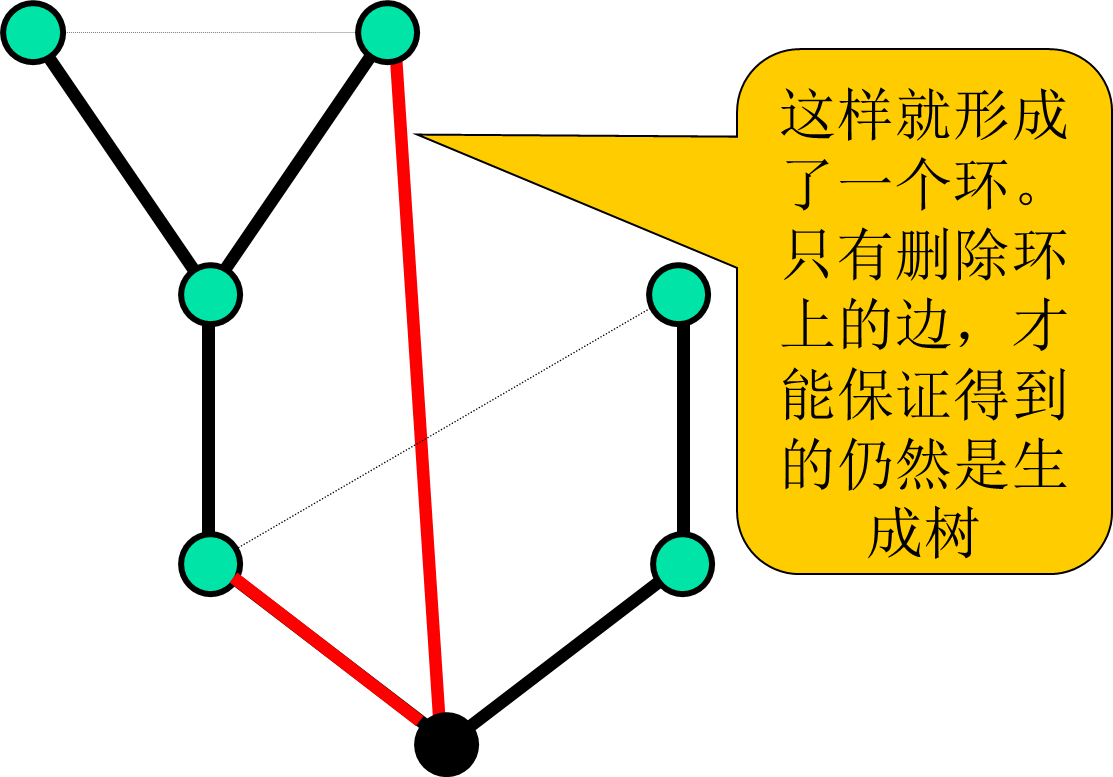
为了使V0的度增加，图中两条边红色的边是不能删除的

删去边的权值越大，所得到的生成树的权值和就越小，因此，需要找到环上可删除的权值最大的边并将其删除。

简单的枚举 但 时间复杂度非常高！！！

造成时间复杂度高的主要原因是有大量的重复计算

用动态规划可以避免大量重复计算

设最小p度限制生成树为T,T是无根树，为了简便，我们把v0作为该树的根。
定义Father(v)为T中v的父结点，Father(v0)无意义。
设Best(v)为路径v0->v上与v0无关联且权值最大的边。

Best(v)的状态转移方程为
Best(v)=max(Best(Father(v)),ω(Father(v),v))

边界条件为
Best[v0]=-∞，Best[v’]=-∞|(v0,v’)∈E(T)。
因为每次寻找的是最大边,所以-∞不会被考虑

状态总共|V|个，而状态转移的时间复杂度为O(1),因而总的时间复杂度是O(V),即通过最小p度限制生成树求最小p+1度限制生成树的时间复杂度是O(V)。

具体实现：从V0开始做一遍搜索即可。
问题：最先求几度的最小度限制生成树呢？即p从多少开始求？

因为求最小k度限制生成树，当 k < DG(v0) 时，问题并不总是有解的。如图。

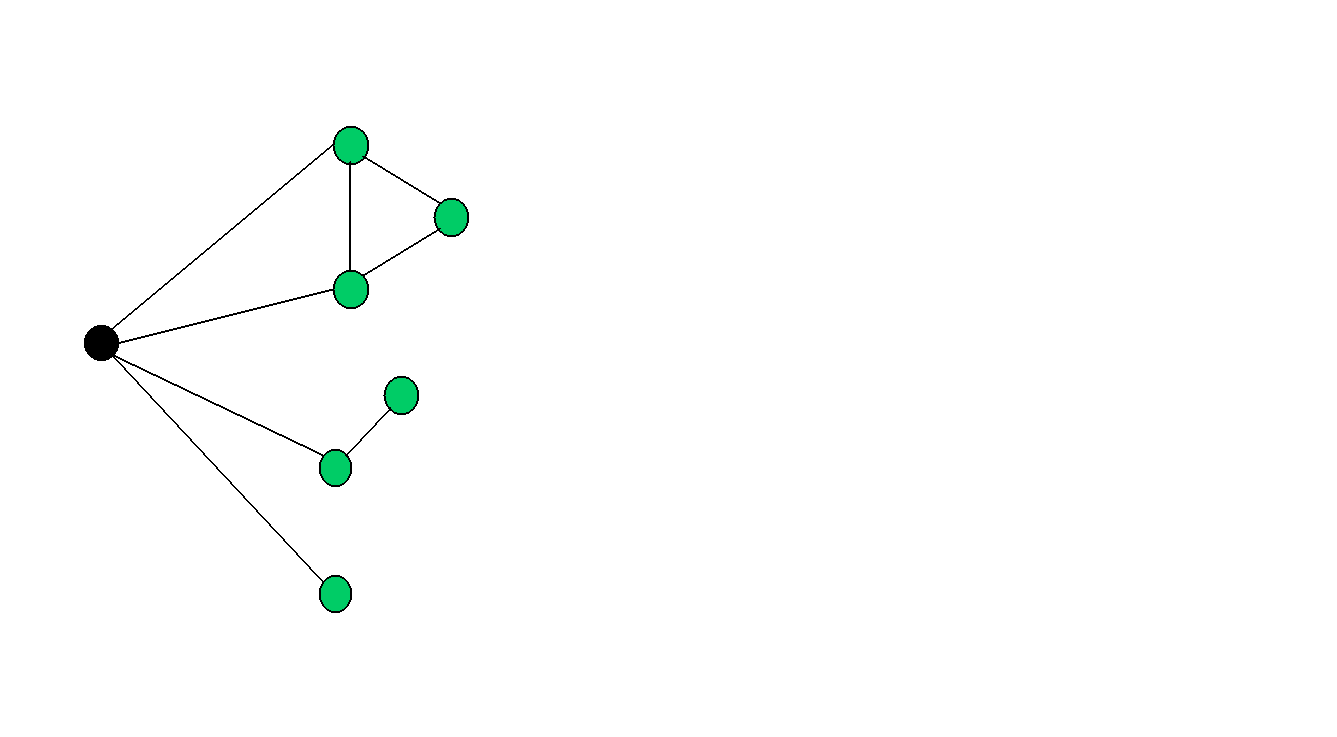
k≤2,不存在k度限制生成树

将v0从图中删去，图中将会出现3个连通分量

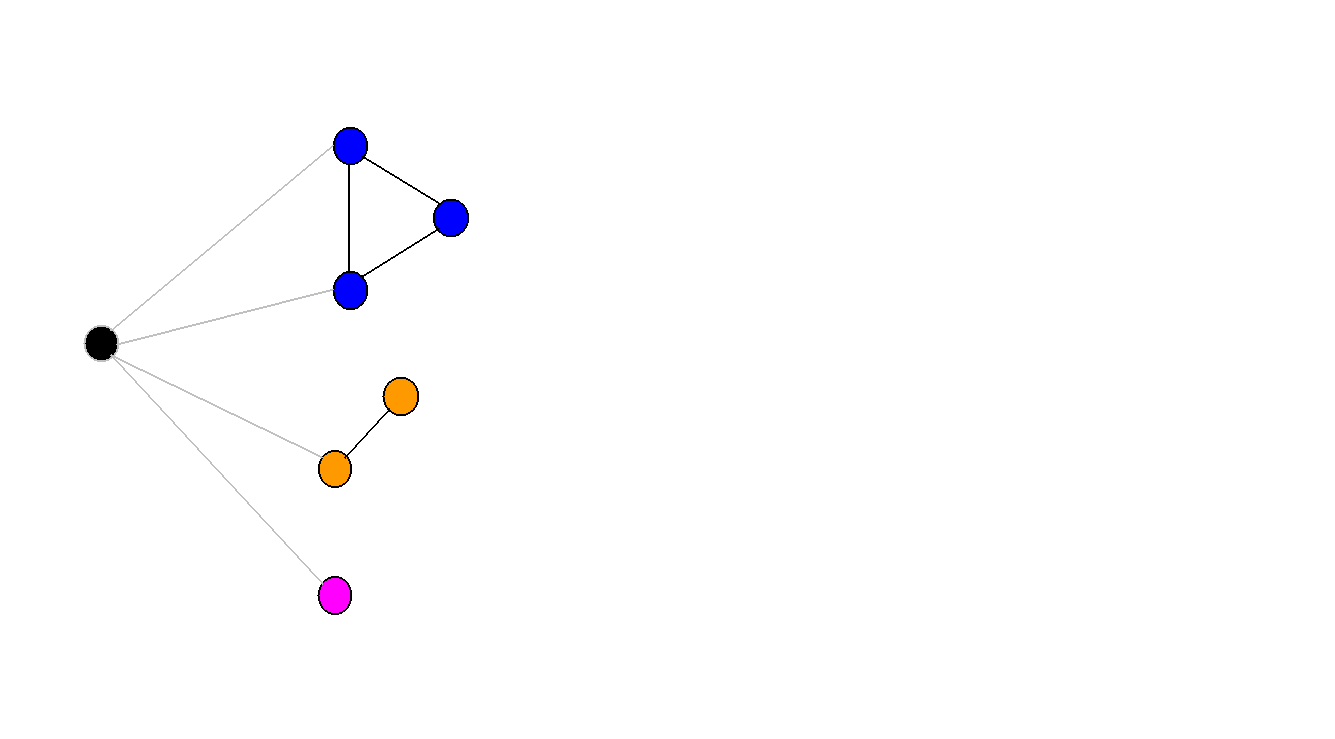
而这3个连通分量必须通过v0来连接，k<3无解

所以如果将v0去掉，图会被分成m个连