C语言实现平衡二叉树的插入与删除

已于 2023-05-16 11:42:29 修改
阅读量756 收藏 11
点赞数
分类专栏： c语言 数据结构与算法 文章标签： 数据结构 算法 c语言
于 2023-05-15 12:55:14 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_21708039/article/details/130682178
版权

目录

前言&看前必读

1.什么是平衡二叉树？

        1.1平衡二叉树的基本概念

         1.2为何要引入平衡二叉树？

2.平衡二叉树如何进行调整？

3.平衡二叉树的插入实现

4.平衡二叉树的删除实现

5.完整代码

前言&看前必读

本文参考b站up@TyrantLucifer，发布的视频教程数据结构-平衡二叉树(AVL)-C语言实现https://www.bilibili.com/video/BV1m64y147Tv/?p=2&vd_source=b64a25bce866a4532d6d87bb174d59e4这个视频讲解通俗易懂，代码可读性也比较高，值得网友去学习。所以本文代码基于此视频教程作为参考，不过这里的代码但略有改动，程序的思路是相同的。另附参考的原文地址：数据结构系列19-平衡二叉树 | tyrantlucifer

本文不讲大量空洞的理论。秉承以实践为主，理论为辅的宗旨讲解平衡二叉树的插入与删除的实现。前面第一节第二节主要是简述一些基本的概念，从第三节开始结合实际讲解程序的思路。如果您对平衡二叉树有了基本的认识可以直接跳到第三节。

个人技术水平有限，如有不妥之处请多多指教，相互交流学习

1.什么是平衡二叉树？

        1.1平衡二叉树的基本概念

                平衡二叉树(balance binary tree)又称作AVL树，AVL树名字来自提出者G.M. Adelson-Velsky和E.M. Landis。平衡二叉树是二叉搜索树的进化体，由此平衡二叉树具有二叉排序树所有的基本特征：

                1.如果左子树不为空，则左子树上任意一个节点值均小于根节点值。

                2.如果右子树不为空，则右子树上任意一个节点值均大于根节点值。

                3.左右子树都是二叉排序树。

                4.树中没有相同的节点。

除此之外，平衡二叉树还具备一个非常重要的特点：任意一个节点左右子树的高度之差的绝对值不超过1，加上前面所提到的四个特征，总共五个特征，缺一不可。我们通常把左右子树的高度差称为平衡因子（BF，Belance Fator），如下面图1所示，这是一颗典型的平衡二叉树。每个节点右上角标记的数是这个节点的平衡因子，显然这颗平衡二叉树具备其应有的所有特征。

        

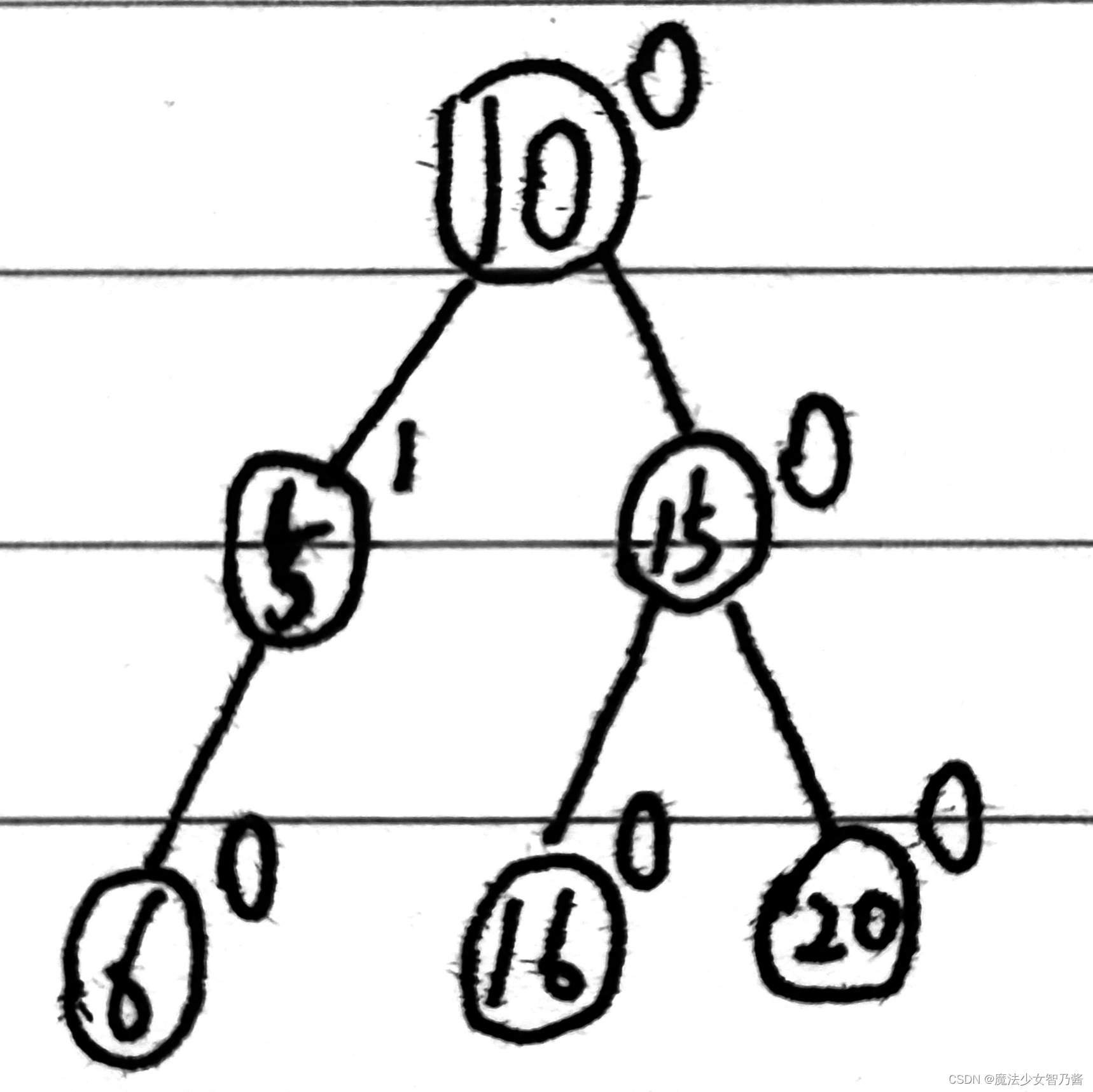
6a6e5204a6d244209bda9c6dc1afbc81.jpeg

图1 平衡二叉树

         1.2为何要引入平衡二叉树？

        二叉排序树的平均查找长度与树的形状有关，最好的情况是O(log2n),最差的情况是O(n),如下图所示，把1 2 3 4 5 这几个元素，按顺序依次插入节点将得到这样的一颗二叉树，如图2所示，此时二叉查找树被退化成链表。显然这个二叉排序树的平均查找长度为O(n)，所以我们需要引入平衡二叉树来解决这一问题，平衡二叉树在插入/删除完成后，会沿着检查其插入/删除路径的每一个节点的平衡因子，当平衡因子BF等于2时会及时做出相应的调整，从而最大程度的避免这种情况发生。

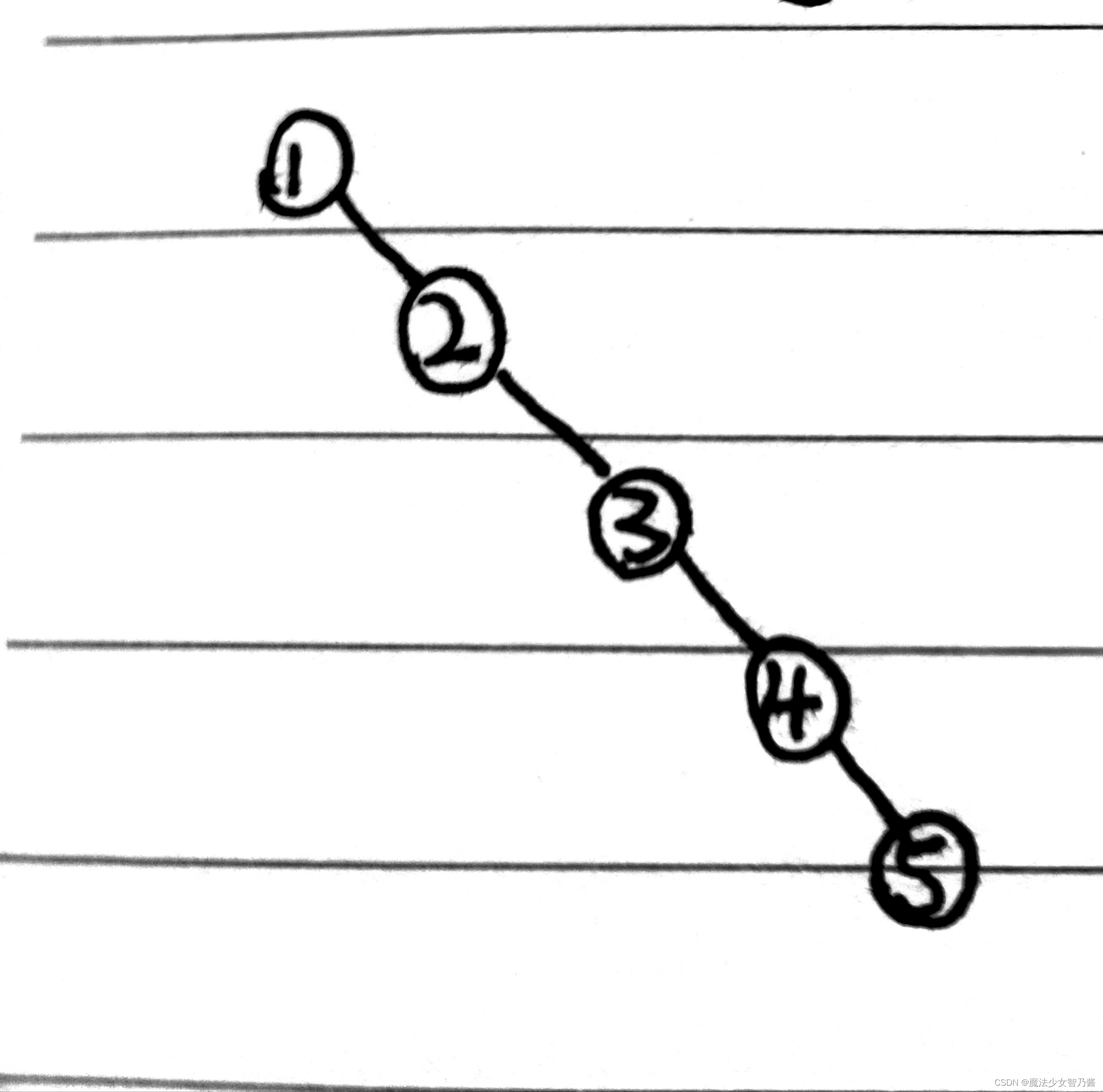
dd13b27101764f4aaf8162594f4d9042.jpeg

图2 退化成链表的二叉排序树

2.平衡二叉树如何进行调整？

                为了方便讲解平衡二叉树如何调整，我们要引入一个概念，即最小不平衡子树，最小不平衡二叉子树的根节点是离插入点最近且平衡因子的绝对值大于1的节点作为根节点的二叉子树，如图3所示的二叉排序树，在此树插入一个新节点90，如左侧所示，左侧原本98的平衡因子绝对值为1，插入后由1变为2，显然98就是最小不平衡二叉子树的根节点。如右边的红色圈圈所示。当然最小不平衡二叉子树有可能的整个二叉树本身，如图5所示，15是二叉树的根节点，它的平衡因子的绝对值为2。

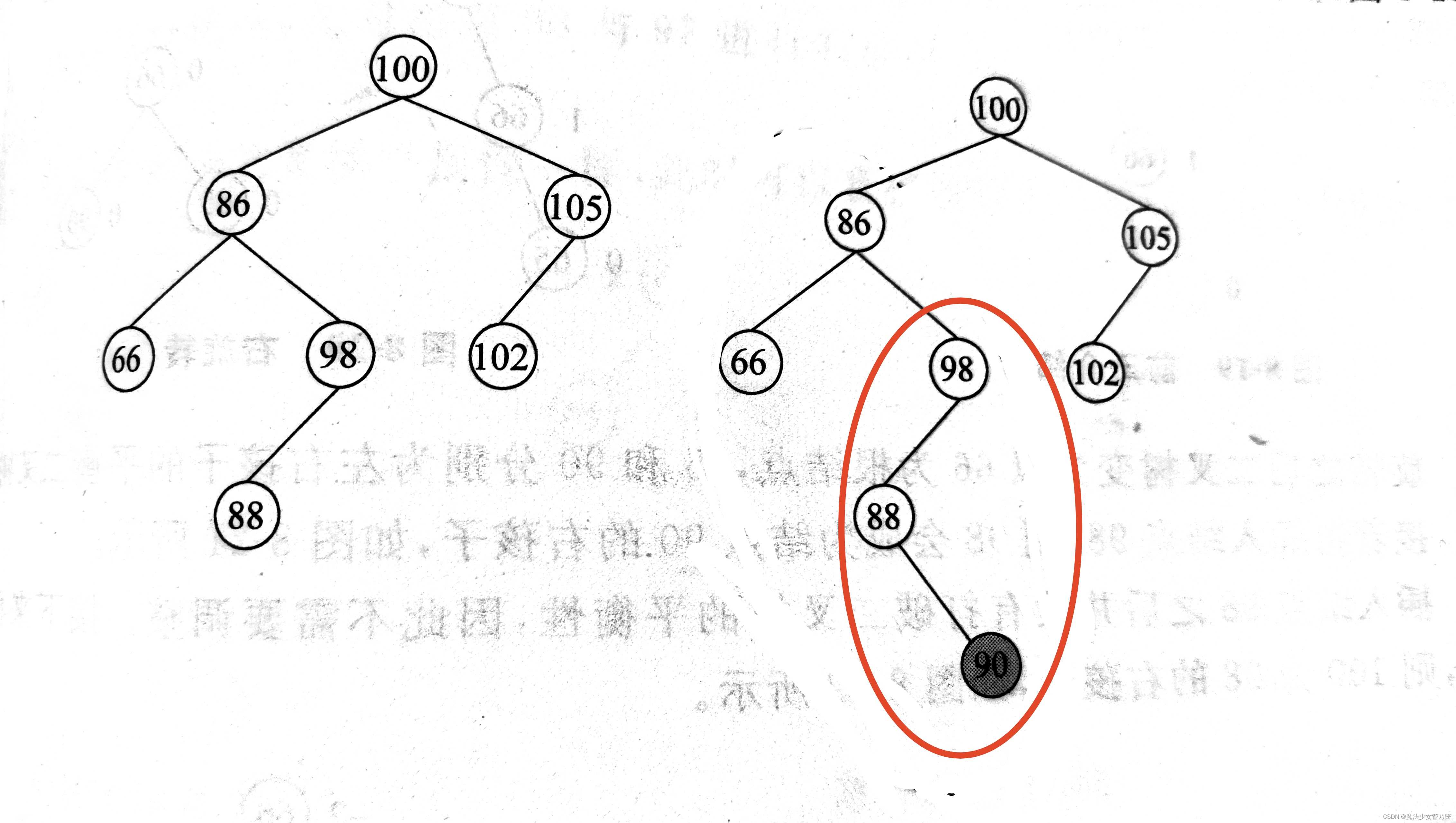
f4558946e64048dd93dae4d51969c2ab.jpeg

图 3 最小不平衡子树

         

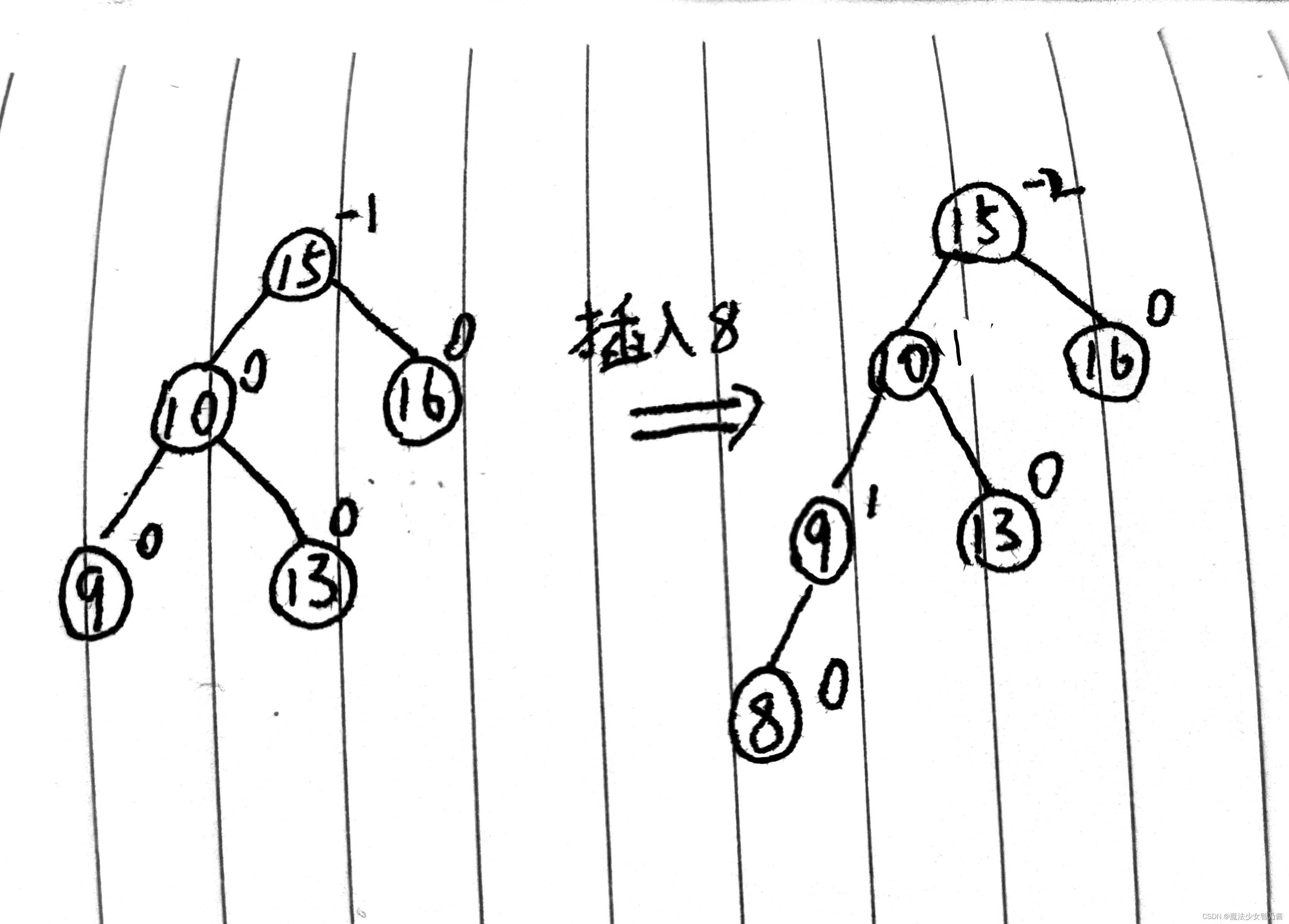
af725f4fcb2346dba9652ea9743af814.jpeg

图5 最小不平衡二叉子树也有可能是根节点

温馨提示：下面简单介绍几种不平衡节点的调整方式，这些内容对编写程序的帮助有限，仅用于了解一些基本的概念，实际调整碰到的情况比较复杂一点，很多情况下只会这些概念编写程序显得有些束手无策，当然如果您对这些调整方式有了基本的认识，可以直接跳到二叉树的插入实现这一节，本文将讲详细讲解其插入删除时调整的原理和细节。

图6-图9看懂大概意思就行了，先不要钻牛角尖，对于平衡二叉树的学习由易到难，才是正确的学习方法，平衡二叉树调整的详细过程请见本文的第三节。平衡二叉树旋转必须要掌握稍微复杂的情况怎么处理，才能独立写出程序来。

对于平衡二叉树来说不平衡节点主要右RR型、LL型、RL型、LR型。导致不平衡节点出现的原因都是新节点插入导致的，所以我们需要对其进行旋转操作。

常见不平衡节点产生的原因以及处理方法

类型原因处理方法
RR新插入节点的插入到不平衡节点的右孩子的右边左旋（图6）
LL新插入节点的插入到不平衡节点的左孩子的左边右旋（图7）
RL新插入节点的插入到不平衡节点的右孩子的左边先右旋再左旋（图8）
LR新插入节点的插入到不平衡节点的左孩子的右边先左旋再右旋（图9）

对于RR型我们需要进行左旋操作，如图6所示：

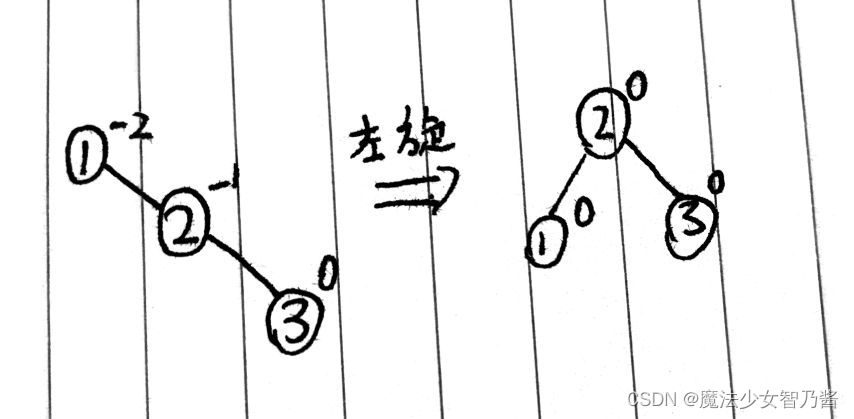
8776ef29c29049f5a06bbf2cd17efbff.jpeg

图6 RR型调整

 对于LL型我们需要进行先右旋操，如图7所示：

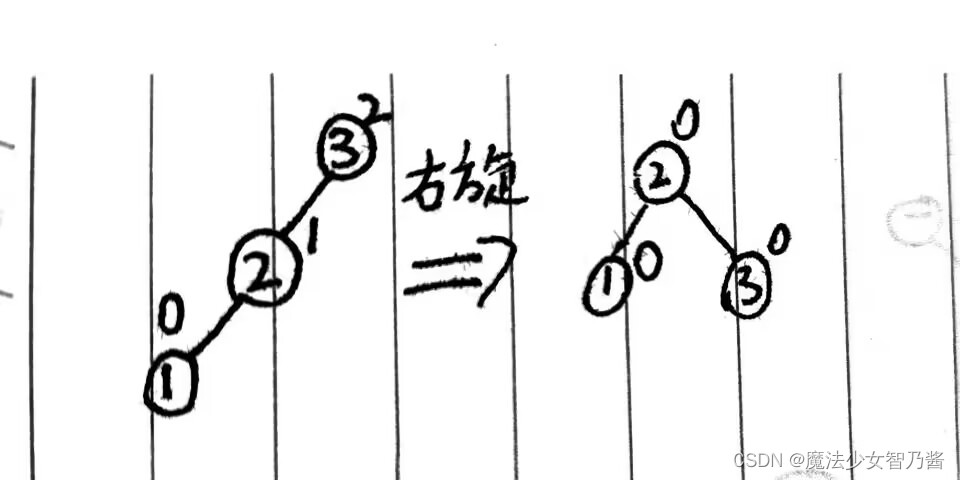
0f092155660f4b8aaa6b3e85f28aea7b.jpeg

图7 LL型调整

  对于RL型我们需要进行先右旋操作，再左旋操作，如图8所示：

   

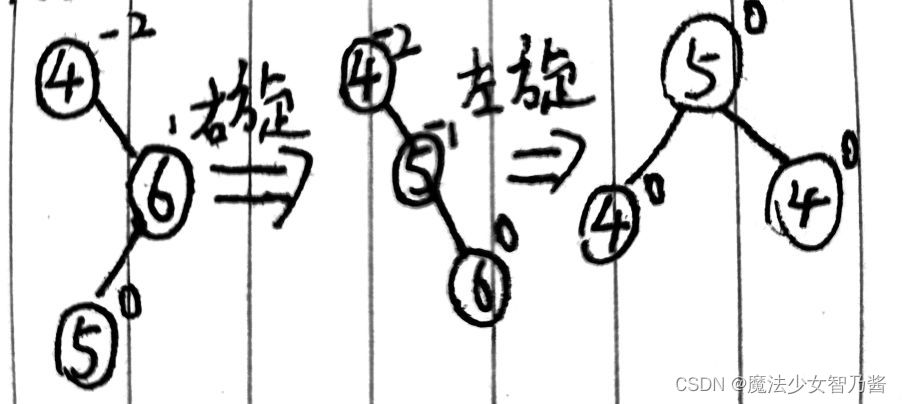
51ff35f583f64b8581a6dca61c6ccd15.jpeg

图8 RL型调整

对于LR型我们需要进行先左旋操作，再右旋操作，如图9所示：

e114feb2a6d94b918b2a2c37d8936619.jpeg

图9 LR型调整

3.平衡二叉树的插入实现

             如图10-图12所示下面分别是稍微复杂情况下调整方法以及各节点平衡因子的情况，通过观察平衡因子的情况有助于我们写程序来判断当前二叉树是否应该要调整。实现平衡二叉树的插入操作首先要实现左旋函数和右旋函数，以确保插入元素后任然具有平衡二叉树的所有特性。

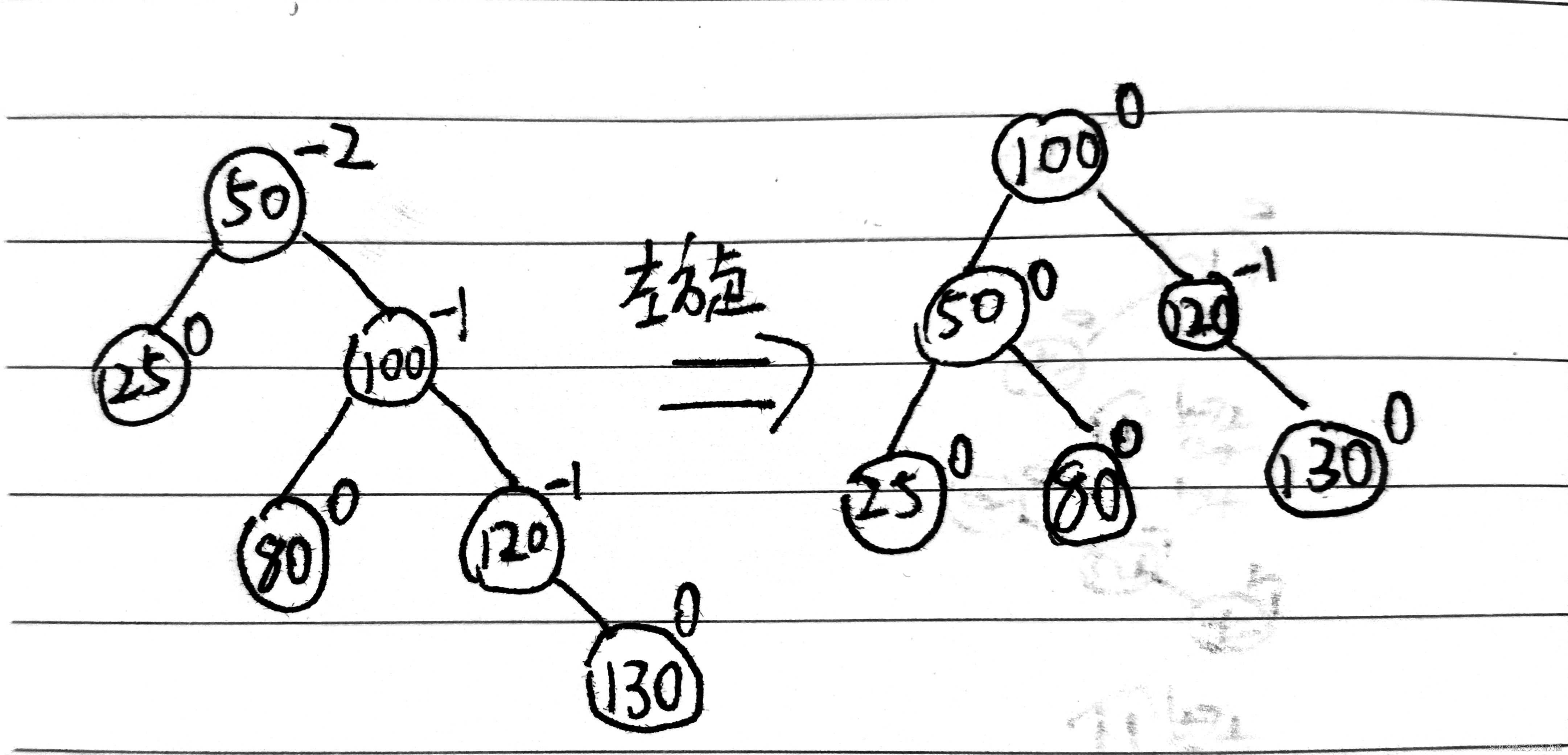
dcba622ab94f4cb69a1d0a59661d2c51.jpeg

图10 稍复杂情况下的RR型的调整

        如图10所示130是最新插入的节点，50是不平衡节点，它的平衡因子(以下将简称BF)为-2，属于RR型，RR型是新节点插入最小不平衡右子树的右子树导致的，因此我们对它进行左旋操作，先做准备工作，创建一个临时变量保存首先把最小不平衡子树的根节点右孩子保存起来，最小不平衡子树的根节点的右孩子指针指向最小不平衡右孩子的左孩子，然后再把最小不平衡子树的根节点的右孩子的左孩子指针指向最小不平衡子树的根节点，最后把最小不平衡子树的根节点的右孩子换做成该子树的根节点。

        或许看着听着有点绕？没关系，看下面的代码并且结合图片更非常的直观的。

  首先定义一个结构体

typedef struct TreeNode
{
	int data;//数据
	int height;//当前节点的高度
	struct TreeNode* lchild;//左孩子
	struct TreeNode* rchild;//右孩子
}TreeNode;

//获取当前节点高度
int getHeight(TreeNode* node)
{
	return node ? node->height : 0;
}
//返回最大值
int max(int a, int b)
{
	return a>b ? a : b;
}

 实现RR型处理的左旋函数

//RR处理，左旋node是根节点指针，root是根节点二级指针
//当然作为读者可以适当优化一些，比如只用一个二级指针就能实现这个功能
void rrRotation(TreeNode *node, TreeNode** root)
{
	TreeNode* temp = node -> rchild;//保存最小不平衡子树根节点的右孩子
	node -> rchild = temp ->  lchild;//根节点右孩子指向，自己右孩子的左孩子
	temp -> lchild = node;//自己右孩子的左孩子指针指向根原来的最小不平衡二叉树的根节点
    //重新节点计算高度
	node -> height = max(getHeight(node -> lchild),getHeight(node -> rchild)) + 1;
	temp -> height = max(getHeight(temp -> lchild),getHeight(temp -> rchild)) + 1;
	//原来的最小不平衡二叉树的根节点的右孩子作为新的根节点
    *root = temp;
}
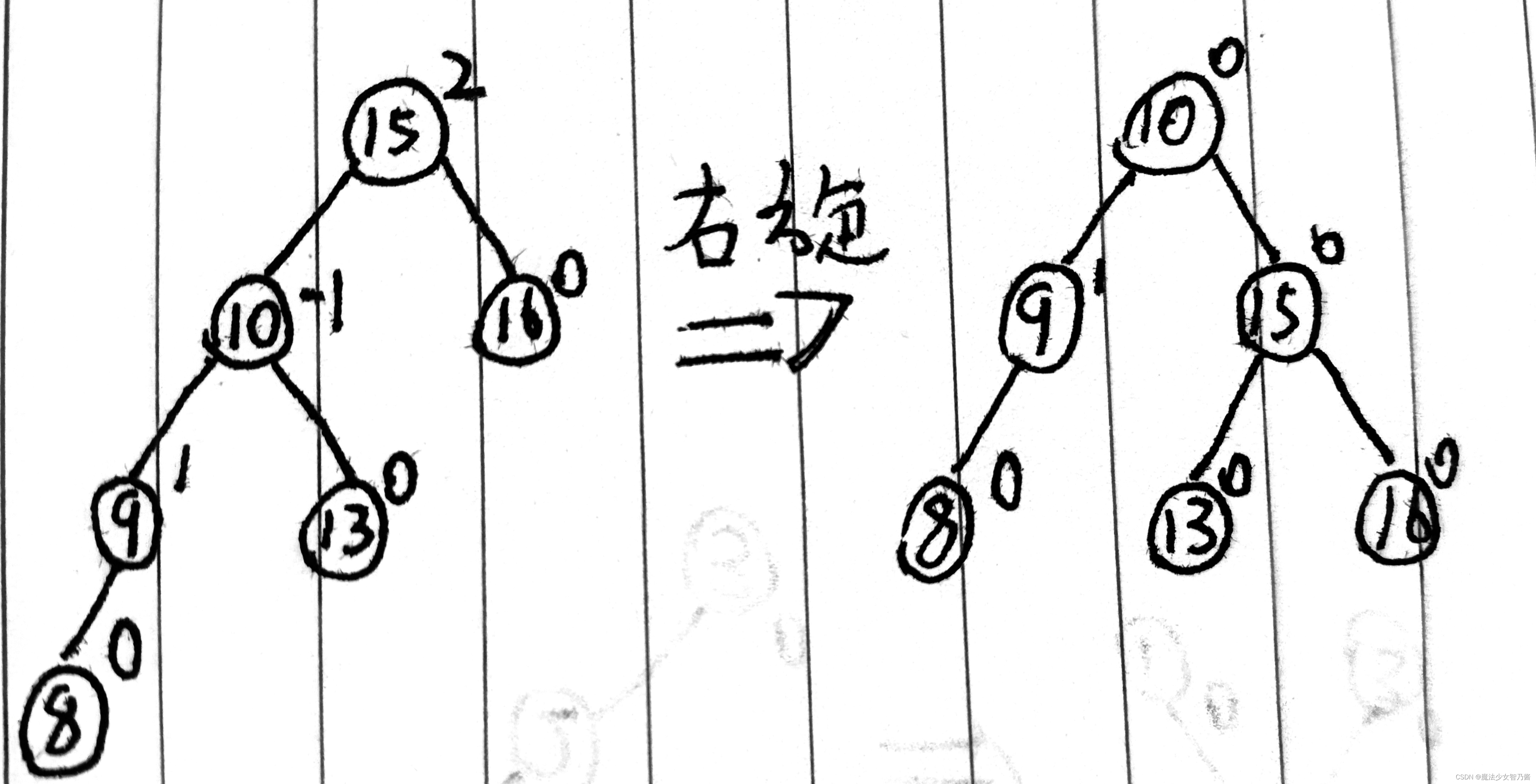
f38a1eba64d8462d82b8920eb346e16c.jpeg

图11 稍复杂情况下的LL型的调整

          如图11所示8是最新插入的节点，15是不平衡节点，它的平衡因子BF为2，属于LL型，LL型是新节点插入最小不平衡左子树的左子树导致的，因此我们对它进行右旋操作，先做准备工作，创建一个临时变量保存首先把最小不平衡子树的根节点左孩子保存起来，最小不平衡子树的根节点的左孩子指针指向最小不平衡左孩子的右孩子，然后再把最小不平衡子树的根节点的左孩子的右孩子指针指向最小不平衡子树的根节点，最后把最小不平衡子树的根节点的左孩子换做成该子树的根节点。

   看下面的代码并且结合图片更非常的直观的。

   实现LL型处理的右旋函数

//LL处理，右旋，node是根节点指针，root是根节点二级指针
//当然作为读者可以适当优化一些，比如只用一个二级指针就能实现这个功能
void llRotation(TreeNode *node, TreeNode** root)
{
	TreeNode *temp =  node ->lchild;//保存最小不平衡子树根节点的左孩子
	node -> lchild = temp->rchild;//根节点左孩子指向自己左孩子的右孩子
	temp -> rchild = node;//自己左孩子的右孩子指针指向根原来的最小不平衡二叉树的根节点
	//更新高度
    node -> height = max(getHeight(node->lchild),getHeight(node->rchild)) + 1;
	temp -> height = max(getHeight(temp -> lchild),getHeight(temp -> rchild)) + 1;
	*root = temp;//左孩子作为根节点
}
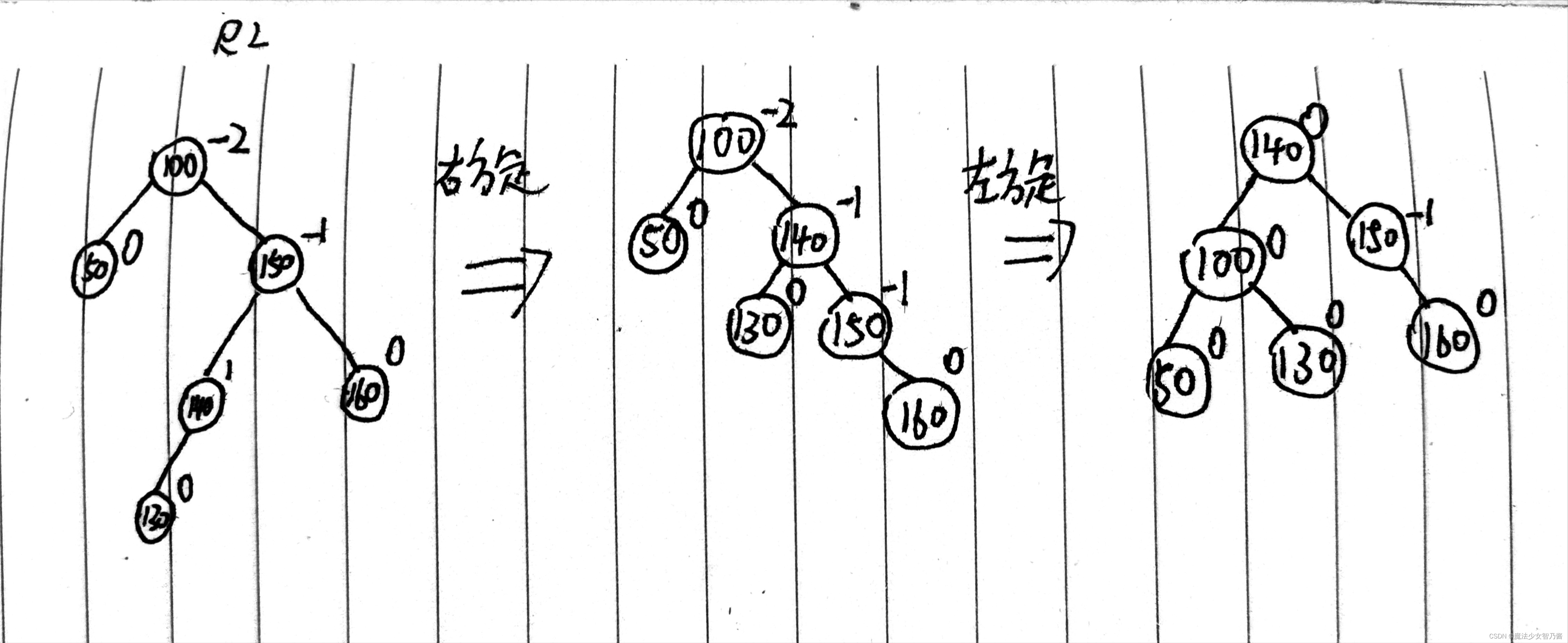
dd0107f5ac49434cac32bc9970db8b5b.jpeg

图12  稍复杂情况下的RL型的调整

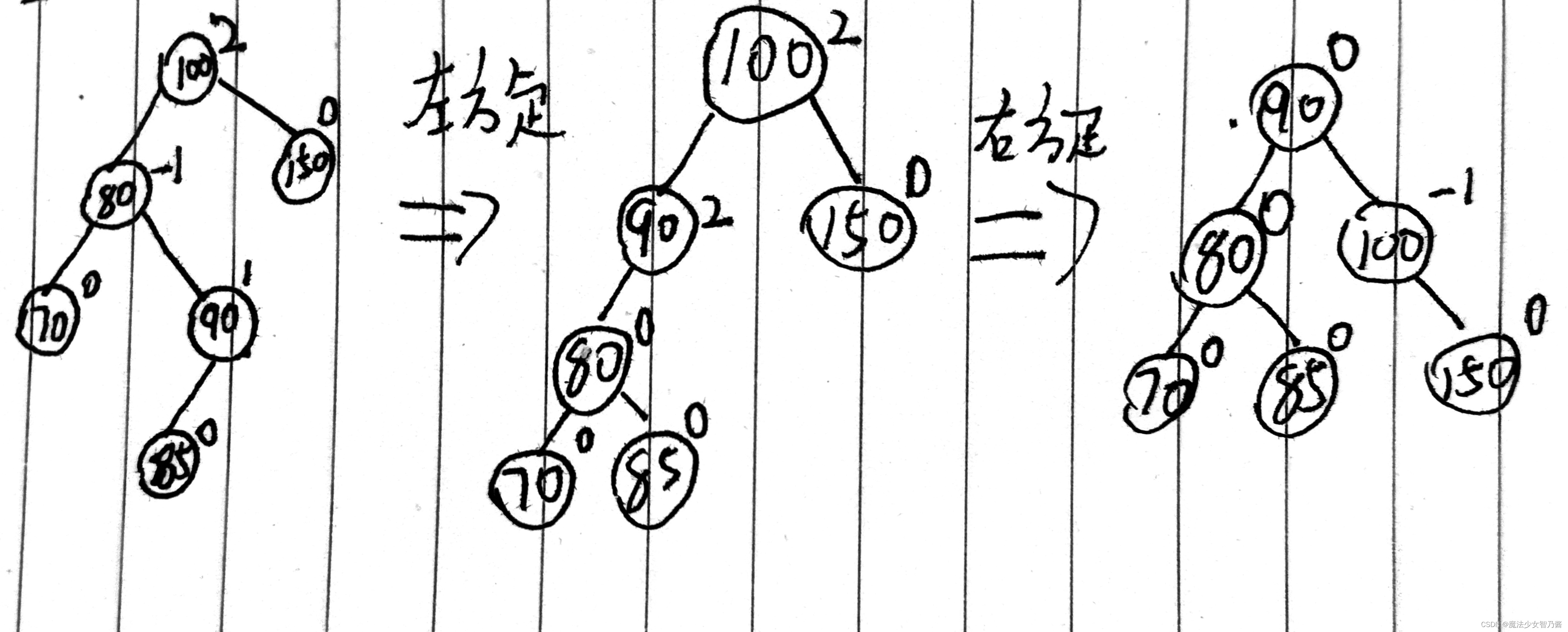
d21af1e2c57b427fa7d367a5dd1eb2f2.jpeg

图13 稍复杂情况下LR调整

 如图13-14所示，RL型很直观的可以看出，先对其最小不平衡子树的右孩子右旋，然后对最小不平衡子树的根左旋。LR型很直观的可以看出，先对其最小不平衡子树的左孩子左旋，然后对最小不平衡子树的根右旋。

       平衡二叉树插入思路

              平衡二叉树的插入基本原理与二叉搜索树相类似，只不过多了一个二叉树调整的步骤，每次插入完后向原路径返回，检查其节点的平衡因子的绝对值是否大于2，如果大于2，则去调整。

        二叉树插入/删除的实现主要是难点是如何判断最小不平衡子树属于哪种类型，一般情况人眼看二叉树不平衡属于哪种类型该如何调整，一眼就能看出来，但是计算机不像人类一样，所以需要梳理好一套清晰的逻辑，才能编写程序来判断并作出相应调整。

        观察图6-图13可知，LL型的新插入的节点总是在当前节点的左孩子的左边，再结合本文第一节所提到的特征，新插入的节点一定比当前不平衡节点的左孩子要小。如果是LR型，新插入的节点总是在当前节点的左孩子的右边，所以比当前节点的左孩子大。RR型新插入的节点一定比当前不平衡节点的右孩子要大，RL型则是相反的，只要利用这个特性就能判断出当前节点不平衡属于什么类型了。

平衡二叉树插入代码如下所示：



//插入
void avlInsert(TreeNode** T, int data)
{
	if(*T == NULL)
	{
		*T = (TreeNode*)malloc(sizeof(TreeNode));
		(*T) -> data = data;
		(*T) -> height = 0;
		(*T) -> lchild = NULL;
		(*T) -> rchild = NULL;
	}else if(data < (*T)->data){

		avlInsert(&(*T)->lchild,data);

		int lHeight = getHeight((*T) -> lchild);
		int rHeight = getHeight((*T) -> rchild);
		//计算平衡因子
		if(lHeight - rHeight == 2)//LL or LR
		{
			if(data < (*T)->lchild->data)
			{
				//LL
				llRotation(*T,T);
			}else{
				//LR
				rrRotation((*T)->lchild,&(*T)->lchild);
				llRotation(*T,T);
			}
		}
	}else if(data > (*T) -> data){// RR or RL
		avlInsert(&(*T) -> rchild, data);
		int lHeight = getHeight((*T)->lchild);
		int rHeight = getHeight((*T)->rchild);
		//计算bf
		if(rHeight - lHeight == 2)
		{
			if(data > (*T) -> rchild -> data)
			{
				//RR
				rrRotation(*T,T);
			}else{
				//RL
				llRotation((*T)->rchild,&(*T)->rchild);
				rrRotation(*T,T);
				
			}
		}
	}
	(*T)->height = max(
						getHeight((*T)->lchild),
						getHeight((*T)->rchild)
					) +1;
}

4.平衡二叉树的删除实现

         平衡二叉树删除的基本原理也是类似的，删除的基本原理和二叉搜索树相同，如果不了解基本原理请参考下面这篇文章：

c语言递归实现二叉排序树的插入与删除https://blog.csdn.net/qq_21708039/article/details/130516473        平衡二叉树的插入和删除也是同样的，删除后需要沿着删除路径检查是否有节点不平衡，也就是计算BF，对此本文采用第二种方法来判断不平衡节点的类型。

        通过观察图6-图13可知，当最小不平衡二叉树的BF是+2说明当前类型可能是LL型或者LR型，这时候我们需要进一步判断他的左子树BF值是多少，当左子树的BF=1或者0是说明是LL型，LR型BF = -1。当最小不平衡二叉树的BF是-2明当前类型可能是RR型或者RL型，这时候我们需要进一步判断他的右子树BF值是多少，当右子树的BF=-1或者0是说明是RR型，RL型BF = 1。

平衡二叉树删除代码如下所示：

//删除
void avlDelete(TreeNode** T, int data)
{
	if(T == NULL)	return;
	if(*T == NULL)	return;
	if(data > (*T)->data)
	{

		avlDelete(&(*T)->rchild,data);
	
	}else if(data < (*T)->data){
	
		avlDelete(&(*T)->lchild,data);

	}else{

		if((*T)->lchild == NULL  && (*T)->rchild == NULL)
		{

			free(*T);
			*T = NULL;
		
		}else if( (*T) -> lchild == NULL ){

			struct TreeNode* temp = (*T)->rchild;
			free(*T);
			*T = temp;
		}else if( (*T) -> rchild == NULL ){

			struct TreeNode* temp = (*T)->lchild;
			free(*T);
			*T = temp;
				
		}else{
			struct TreeNode* temp = (*T)->lchild;
			while(temp -> rchild != NULL)
			{
				temp = temp ->rchild;
			}
			(*T)->data = temp->data;
			avlDelete(&(*T)->lchild,temp->data);
		}

	}

		if(*T == NULL) return;//如果删除后是空指针就什么都不做
		(*T)->height = max(
					
					getHeight((*T)->lchild),
					getHeight((*T)->rchild)
				
				)+1;
		int lheight = getHeight((*T)->lchild);
		int rheight = getHeight((*T)->rchild);
        //计算BF
		if(lheight-rheight == 2)
		{
			//LL LR
            //进一步判断，详见上文
			if( getHeight((*T)->lchild->lchild) - getHeight((*T)->lchild->rchild) == 0 ||  getHeight((*T)->lchild->lchild) - getHeight((*T)->lchild->rchild) == 1 )
			{
				//LL
				
				llRotation(*T,T);
			}else{
				//LR
			
				rrRotation((*T)->lchild, &(*T)->lchild);
				llRotation(*T,T);
			}

		}else if(lheight -rheight == -2)
		{
			//RR RL	
			if( getHeight((*T)->rchild->lchild) - getHeight((*T)->rchild->rchild) == 0 ||  getHeight((*T)->rchild->lchild) - getHeight((*T)->rchild->rchild) == -1 )
			{
				//RL
				rrRotation(*T,T);
			}else{

				//RL
				llRotation((*T)->rchild,&(*T)->rchild);
				rrRotation(*T,T);
			}

		}
}

        

5.完整代码

#include<stdlib.h>
#include<stdio.h>

typedef struct TreeNode
{
	int data;
	int height;
	struct TreeNode* lchild;
	struct TreeNode* rchild;
}TreeNode;

int getHeight(TreeNode* node)
{
	return node ? node->height : 0;
}

int max(int a, int b)
{
	return a>b ? a : b;
}

void rrRotation(TreeNode *node, TreeNode** root)
{
	TreeNode* temp = node -> rchild;
	node -> rchild = temp ->  lchild;
	temp -> lchild = node;
	node -> height = max(getHeight(node -> lchild),getHeight(node -> rchild)) + 1;
	temp -> height = max(getHeight(temp -> lchild),getHeight(temp -> rchild)) + 1;
	*root = temp;
}

void llRotation(TreeNode *node, TreeNode** root)
{
	TreeNode *temp =  node ->lchild;
	node -> lchild = temp->rchild;
	temp -> rchild = node;
	node -> height = max(getHeight(node->lchild),getHeight(node->rchild)) + 1;
	temp -> height = max(getHeight(temp -> lchild),getHeight(temp -> rchild)) + 1;
	*root = temp;
}

void avlInsert(TreeNode** T, int data)
{
	if(*T == NULL)
	{
		*T = (TreeNode*)malloc(sizeof(TreeNode));
		(*T) -> data = data;
		(*T) -> height = 0;
		(*T) -> lchild = NULL;
		(*T) -> rchild = NULL;
	}else if(data < (*T)->data){

		avlInsert(&(*T)->lchild,data);

		int lHeight = getHeight((*T) -> lchild);
		int rHeight = getHeight((*T) -> rchild);
		//计算平衡因子
		if(lHeight - rHeight == 2)
		{
			if(data < (*T)->lchild->data)
			{
				//LL
				llRotation(*T,T);
			}else{
				//LR
				rrRotation((*T)->lchild,&(*T)->lchild);
				llRotation(*T,T);
			}
		}
	}else if(data > (*T) -> data){
		avlInsert(&(*T) -> rchild, data);
		int lHeight = getHeight((*T)->lchild);
		int rHeight = getHeight((*T)->rchild);
		//计算bf
		if(rHeight - lHeight == 2)
		{
			if(data > (*T) -> rchild -> data)
			{
				//RR
				rrRotation(*T,T);
			}else{
				//RL
				llRotation((*T)->rchild,&(*T)->rchild);
				rrRotation(*T,T);
				
			}
		}
	}
	(*T)->height = max(
						getHeight((*T)->lchild),
						getHeight((*T)->rchild)
					) +1;
}


void avlDelete(TreeNode** T, int data)
{
	if(T == NULL)	return;
	if(*T == NULL)	return;
	if(data > (*T)->data)
	{

		avlDelete(&(*T)->rchild,data);
	
	}else if(data < (*T)->data){
	
		avlDelete(&(*T)->lchild,data);

	}else{

		if((*T)->lchild == NULL  && (*T)->rchild == NULL)
		{

			free(*T);
			*T = NULL;
		
		}else if( (*T) -> lchild == NULL ){

			struct TreeNode* temp = (*T)->rchild;
			free(*T);
			*T = temp;
		}else if( (*T) -> rchild == NULL ){

			struct TreeNode* temp = (*T)->lchild;
			free(*T);
			*T = temp;
				
		}else{
			struct TreeNode* temp = (*T)->lchild;
			while(temp -> rchild != NULL)
			{
				temp = temp ->rchild;
			}
			(*T)->data = temp->data;
			avlDelete(&(*T)->lchild,temp->data);
		}

	}
		if(*T == NULL) return;
		(*T)->height = max(
					
					getHeight((*T)->lchild),
					getHeight((*T)->rchild)
				
				)+1;
		int lheight = getHeight((*T)->lchild);
		int rheight = getHeight((*T)->rchild);
		if(lheight-rheight == 2)
		{
			//LL LR
			if( getHeight((*T)->lchild->lchild) - getHeight((*T)->lchild->rchild) == 0 ||  getHeight((*T)->lchild->lchild) - getHeight((*T)->lchild->rchild) == 1 )
			{
				//LL
				
				llRotation(*T,T);
			}else{
				//LR
			
				rrRotation((*T)->lchild, &(*T)->lchild);
				llRotation(*T,T);
			}

		}else if(lheight -rheight == -2)
		{
			//RR RL	
			if( getHeight((*T)->rchild->lchild) - getHeight((*T)->rchild->rchild) == 0 ||  getHeight((*T)->rchild->lchild) - getHeight((*T)->rchild->rchild) == -1 )
			{
				//RL
				rrRotation(*T,T);
			}else{

				//RL
				llRotation((*T)->rchild,&(*T)->rchild);
				rrRotation(*T,T);
			}

		}
}

void preOrder(TreeNode *T)
{
	if(!T) return;
	printf("%d ", T->data);
	preOrder(T -> lchild);
	preOrder(T -> rchild);
}


void inOrder(TreeNode *T)
{
	if(!T) return;
	inOrder(T -> lchild);
	printf("%d ", T->data);
	inOrder(T -> rchild);
}

void bstFree(TreeNode** T)
{
	if(*T == NULL) return;
	 bstFree(&(*T)->lchild);
	 bstFree(&(*T)->rchild);
	 free(*T);
	 *T=NULL;
}


int main()
{
	TreeNode *T = NULL;
	int nums[5] = {1,8,6,7,10};
	for(int i = 0; i<5; i++)
	{
		avlInsert(&T,nums[i]);
	}

	preOrder(T);
	printf("\t先\n");
	inOrder(T);
	printf("\t中\n");

	avlDelete(&T,6);
	preOrder(T);
	printf("\t先\n");
	inOrder(T);
	printf("\t中\n");
	
	bstFree(&T);
	
	return 0;
}

 运行结果：

6 1 8 7 10 	先
1 6 7 8 10 	中
8 1 7 10 	先
1 7 8 10 	中

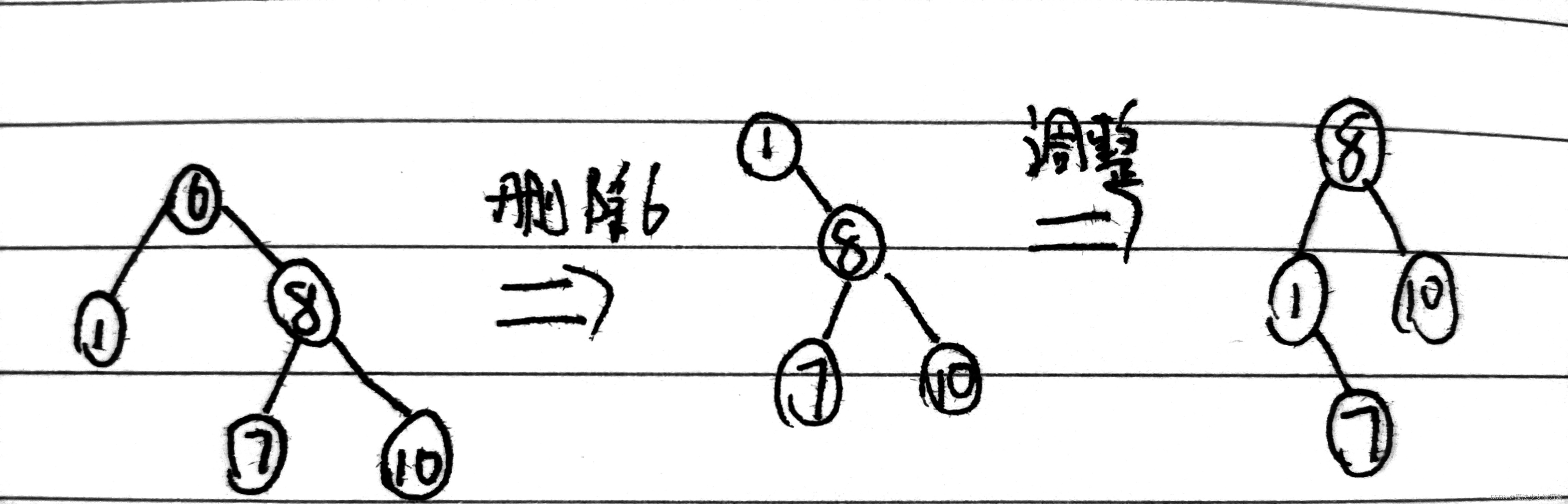
3df171b79e5946bdbb7f1c3303ff44c3.jpeg

图14 上面程序的平衡二叉树的调整过程

魔法少女智乃酱
关注
  • 0
    点赞
  • 踩
  • 11
    收藏
    觉得还不错? 一键收藏
  • 2
    评论
专栏目录
平衡二叉树之C语言实现（插入、删除，分裂、合并）附源代码
GDUT小铭的博客
01-26 4659
平衡二叉树的定义 平衡二叉查找树( Balanced Binary Sort Tree,BBST)简称平衡二叉树。平衡二又树有很多种,其中最著名的是由前苏联数学家 Adele- Veliki和 Landis在1962年提出的高度平衡的二叉树。根据提出者的英文名字首字母简称为AVL树 。 平衡二叉树或者是棵空树,或者是具有下列性质的二叉查找树：它的左子树和右子树都是平衡二叉树，且左...
平衡二叉树的c语言实现
10-15
本代码用c语言实现了平衡二叉树这一数据结构，同时实现了基本查找，插入，删除操作，都是自己精心设计的算法，花了很多功夫。。
平衡二叉树（AV树） 插入和删除 （C语言实现）
m0_58381606的博客
04-17 790
一种特殊的二叉查找树，它的左右子树的高度差不超过1，可以保证树的高度始终在log2(n)级别，从而保证了平衡二叉树的查找、插入、删除操作的时间复杂度都是O(logn)。常见的平衡二叉树有红黑树、AVL树等。AVL树的插入和删除操作都需要进行旋转操作来维护树的平衡，插入和删除的时间复杂度均为O(logn)。
平衡二叉树的创建、插入和删除操作 C语言实现
最新发布
jiekegiao的博客
03-24 1381
当二叉搜索树中的节点按照某种顺序插入，导致树的一边过长，另一边过短时，树就会变得不平衡。不平衡的二叉搜索树在插入、删除和查找操作时，效率会降低，最坏情况下会变成一条线性链表，时间复杂度变为O(n)。为了解决这一问题，和二叉搜索树进行优化，提出了平衡二叉树这一概念平衡二叉树，也称为AVL树或高度平衡的二叉搜索树。在平衡二叉树中，任何一个节点的两个子树的高度差都不超过1，这使得它特别适合用于排序和查找操作。平衡二叉树的节点除了包含值、左子节点和右子节点的指针，还增加了一个高度值。
二叉平衡树(AVL树)插入、删除的C语言实现
sjg_sjk的博客
05-18 3426
对于AVL树的定义，在教科书和网上的资料都已经十分详细，在这里直接上代码，不做过多赘述。AVL树的结构体定义：typedef struct AVLTREE { int data; int height; struct AVLTREE* leftChlid; struct AVLTREE* rightChild; }AVLTREE;其中data为节点的值，而height为节点的高度...
平衡二叉树的定义及基本操作（查找、插入、删除）及代码实现
薛定谔的猫的博客
08-12 4204
文章目录平衡二叉树的定义平衡二叉树的插入 平衡二叉树的定义  为了避免树的高度增长过快，降低二叉排序树的性能，我们规定在插入和删除二叉树结点时，要保证在任意结点的左、右子树高度差的绝对值不超过1，将这样的树称为平衡二叉树（Balanced Binary Tree），简称平衡树（AVL）。  定义结点左子树与右子树的高度差为该结点的平衡因子，则平衡二叉树结点的平衡因子的值只可能是-1，0或1 。 平衡二叉树可定义为：  或者是一棵空树，或者是具有下列性质的二叉树：它的左子树和右子树都是平衡二叉树，且左子树和
数据结构——平衡二叉树之删除
weixin_57023347的博客
07-08 9066
目录 前言 删除结点 调整结点 代码实现 前言 我们知道，在平衡二叉树中插入一个结点可能会改变二叉树的平衡因子，使得平衡因子超过1。但是删除平衡二叉树的一个结点时也会使得二叉树的平衡因子发生改变。也会需要对树进行调整。这篇博客是说明怎么判断调整位置。想了解调整的具体细节的可以看博客数据结构——平衡二叉树(AVL树)之插入。 平衡二叉树删除结点和插入操作类似，首先先删除一个结点，然后对自下向上最近的平衡因子超过1的结点进行调整。 删除结点 首先...
平衡二叉树（AVL树）和 二叉排序树转化为平衡二叉树 及C语言实现
m0_49062515的博客
12-09 2207
平衡二叉树，又称为 AVL 树。实际上就是遵循以下两个特点的二叉树： 每棵子树中的左子树和右子树的深度差不能超过 1； 二叉树中每棵子树都要求是平衡二叉树； 其实就是在二叉树的基础上，若树中每棵子树都满足其左子树和右子树的深度差都不超过 1，则这棵二叉树就是平衡二叉树。 平衡因子：每个结点都有其各自的平衡因子，表示的就是其左子树深度同右子树深度的差。平衡二叉树中各结点平衡因子的取值只可能是：0、1 和 -1。 如图 1 所示，其中 （a） 的两棵二叉树中由于各个结点的平衡因子数的绝对值都不超过 1，所
c语言平衡二叉树代码示例
12-21
平衡二叉树大部分操作和二叉查找树类似，主要不同在于插入删除的时候平衡二叉树的平衡可能被改变，并且只有从那些插入点到根结点的路径上的结点的平衡性可能被改变，因为只有这些结点的子树可能变化。 平衡二叉树的...
C语言数据结构之平衡二叉树（AVL树）实现方法示例
12-26
本文实例讲述了C语言数据结构之平衡二叉树（AVL树）实现方法。分享给大家供大家参考，具体如下： AVL树是每个结点的左子树和右子树的高度最多差1的二叉查找树。 要维持这个树，必须在插入和删除的时候都检测是否出现...
C语言实现的AVL平衡二叉树
03-21
用C语言实现了AVL平衡二叉树。主要包括创建新二叉树，插入节点，删除节点，平衡旋转，复制树结构，求并集（union），求交集（intersection），遍历和打印二叉树以及清理内存等。
二叉查找树的C语言实现——插入，删除，查找
11-21
二叉查找树的C语言实现，实现功能：插入、删除、查找。
平衡树(Splay) 服务:第二弹——插入，删除，查询
artalter的博客
03-20 967
平衡树(Splay) 服务:第二弹——插入，删除，查询 0.前言 今天有奥赛课，所以我又回来了 今天会把普通平衡树的操作讲完 1.插入 首先，在splay中，是不会有权值（也就是平衡树排大小的关键字）重复的结点的。取而代之的，是表示这个值出现次数的附加值cnt. 插入操作可以分为几种情况： 1.平衡树中什么也没有，这个时候我们只要新建第一个结点，并把它设为根节点就可以啦。 2.平衡树中已经出现过了这个权值。我们找到这个权值所在的位置，把这个结点的size值和cnt值都加一即可 3.这个权值在平衡树中还没有出
平衡二叉树（AVL树）构造、添加/删除元素(Java)
pikachu_plus的博客
08-21 671
在计算机科学中，AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1，所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis，他们在1962年的论文《An algorithm for the organization of information》中发表了它。——百度百科。
平衡二叉树的删除
weixin_57023347的博客
09-05 1186
目录 前言 一.结点定义 二.删除 2.1 按照二叉搜索树来删除结点 2.2 更新平衡因子 2.3 检测更新完的平衡因子 三.完整代码 前言 之前再C语言阶段学习了平衡二叉树，用C语言递归实现了一下平衡二叉树的删除与插入。实现如下：数据结构——平衡二叉树(AVL树)之插入和数据结构——平衡二叉树之删除当时学习的时候感觉比较费劲，并且难以理解。 现在在C++阶段又重新学习了一下平衡二叉树，使用非递归实现，再加上结点引入平衡因子和父节点，感觉更好理解了。 ...
使用C#操作二叉树的插入查询遍历和打印（代码）
王佳宇的个人博客
11-07 6213
关于二叉树详细介绍请移步：https://blog.csdn.net/weixin_40165163/article/details/83826223 Node类： public class Node { public int Item { set; get; } //节点数据 public Node LeftChild { set; get; ...
数据结构-二叉查找（排序）树的插入，创建，查找，删除（含全部代码）
关注网络安全、云原生安全
01-18 8358
主要函数： BST_Insert(BSTree &T, TElemType data) 参数T，二叉查找树根节点 作用：插入数据data,保证中序非严格递增（即可重复） PreOrder(BSTree T) 参数T，二叉查找树根节点 作用：先序遍历二叉查找树，递归方式 InOrder(BSTree T) 参数T，二叉查找树根节点 作用：中序遍历二叉查找树，递归方式 PostOrd...
《算法导论》12.3 二叉搜索树插入和删除（含有C++代码）
Toby的博客
09-06 540
本文为《算法导论》12.3 二叉搜索树插入和删除的笔记，附有完整代码哦，欢迎参考，期待您的关注！
二叉树删除结点 c语言,平衡二叉树的 插入 删除 查找 等功能c语言实现 数据结构...
weixin_27303545的博客
05-21 152
#include#include #include //左子树比右子树高一#define LH 1//左子树和右子树一样高#define EH 0//左子树比右子树低一#define RH -1#define EQ(a,b) ((a) == (#include#include#include//左子树比右子树高一#define LH 1//左子树和右子树一样高#define EH 0//左子树比右...
数据结构二叉树实验代码
05-31
好的，我可以提供一份二叉树实验代码的示例，供你参考。以下是一个简单的二叉树实现，包括节点的结构体定义、创建、遍历、插入和删除操作等。 ``` #include <stdio.h> #include <stdlib.h> // 二叉树节点结构体定义 typedef struct TreeNode { int val; struct TreeNode *left; struct TreeNode *right; } TreeNode; // 创建二叉树 TreeNode *createTree() { TreeNode *root = NULL; int val; printf("请输入二叉树的根节点值："); scanf("%d", &val); if (val == -1) { // 输入-1表示结束 return NULL; } root = (TreeNode *)malloc(sizeof(TreeNode)); root->val = val; root->left = createTree(); // 递归创建左子树 root->right = createTree(); // 递归创建右子树 return root; } // 前序遍历二叉树 void preorderTraversal(TreeNode *root) { if (root == NULL) { return; } printf("%d ", root->val); preorderTraversal(root->left); preorderTraversal(root->right); } // 中序遍历二叉树 void inorderTraversal(TreeNode *root) { if (root == NULL) { return; } inorderTraversal(root->left); printf("%d ", root->val); inorderTraversal(root->right); } // 后序遍历二叉树 void postorderTraversal(TreeNode *root) { if (root == NULL) { return; } postorderTraversal(root->left); postorderTraversal(root->right); printf("%d ", root->val); } // 插入节点 void insertNode(TreeNode *root, int val) { if (root == NULL) { return; } if (val < root->val) { // 插入左子树 if (root->left == NULL) { TreeNode *node = (TreeNode *)malloc(sizeof(TreeNode)); node->val = val; node->left = NULL; node->right = NULL; root->left = node; } else { insertNode(root->left, val); } } else { // 插入右子树 if (root->right == NULL) { TreeNode *node = (TreeNode *)malloc(sizeof(TreeNode)); node->val = val; node->left = NULL; node->right = NULL; root->right = node; } else { insertNode(root->right, val); } } } // 删除节点 TreeNode *deleteNode(TreeNode *root, int val) { if (root == NULL) { return NULL; } if (val < root->val) { // 在左子树中删除 root->left = deleteNode(root->left, val); } else if (val > root->val) { // 在右子树中删除 root->right = deleteNode(root->right, val); } else { // 找到了要删除的节点 if (root->left == NULL) { // 只有右子树 TreeNode *temp = root->right; free(root); return temp; } else if (root->right == NULL) { // 只有左子树 TreeNode *temp = root->left; free(root); return temp; } else { // 左右子树都存在 TreeNode *temp = root->right; while (temp->left != NULL) { temp = temp->left; } root->val = temp->val; root->right = deleteNode(root->right, temp->val); } } return root; } // 主函数 int main() { TreeNode *root = NULL; int val; root = createTree(); // 创建二叉树 printf("前序遍历："); preorderTraversal(root); // 前序遍历 printf("\n中序遍历："); inorderTraversal(root); // 中序遍历 printf("\n后序遍历："); postorderTraversal(root); // 后序遍历 printf("\n请输入要插入的节点值："); scanf("%d", &val); insertNode(root, val); // 插入节点 printf("插入后的中序遍历："); inorderTraversal(root); // 中序遍历 printf("\n请输入要删除的节点值："); scanf("%d", &val); root = deleteNode(root, val); // 删除节点 printf("删除后的中序遍历："); inorderTraversal(root); // 中序遍历 return 0; } ``` 以上是一个简单的二叉树实现示例，你可以根据自己的需求进行修改和扩展。

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论 2
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值