所有节点对最短路径

一些约定：用d(i,j)表示节点i到节点j的最短路径,w(i,j)表示节点i到节点j的权重；
对于n个节点的图，采用邻接矩阵的方式输入输出，输出及中间结果的矩阵也是n*n的矩阵，第i行j列表示从i到j的当前最短路径

我们这里讲解三个算法，第一个是利用传统的动态规划，第二个也是个动态规划算法，但是基于一种观察结果，他就是warshall算法，第三个算法是将问题转换为没有负数权重的图，再对每个节点调用Dijkstra算法，他就是Johnson算法。

注意：通常情况下我们只用warshall算法，其他两个算法一个效率太低，一个写起来太麻烦。

动态规划求所有节点对最短路径

适用条件：
没有负环（可有负权重）

动态规划步骤：
1.分析最优解的结构
（最短路径结构）
根据最短路径的最优子结构性质，有d(i,j) = d(i,k) + w(k,j)

2.递归定义最优解的值
(所有节点对最短路径问题的递归解)
首先要获取递归求解的对象表达式

这里采取最短路径的边数作为递归的计数对象，因为图中没有负环，所以对于边数大于n-1的最短路径计算也就没有意义（因为n-1条边已经能够将所有节点连接，一旦大于n-1条边则会形成环，并且所有的环都是正权重，所以会使结果变大），因此我们递归时控制边数m使其m>0 && m < n。m=1时，即为输入的邻接矩阵M。

在递归时，我们计算边数为m的最短路径时，将m-1的最短路径与d(i,j) = d(i,k) + w(k,j)进行比较，取最小值。因为k=j时，即为m-1的最短路径，因此问题简化为循环遍历k求d(i,j) = d(i,k) + w(k,j)的最小值。如下图公式：

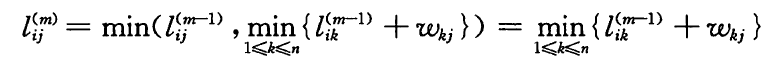
3.自底向上计算最优解的值
（自底向上计算最短路径权重）
因为含有m条边的距离是在m-1条边的基础上计算出来的，所以从含有一条边开始，自底向上求值，按照第二步所述编写代码，详见具体代码。

4.从计算出的最优解的值上构建最优解
按照正常步骤，按部就班的每次递归m++；这样最终的时间复杂度为O(n^4)。但我们要的是最终m=n-1的结果，而对中间结果不感兴趣，因此我们可以使m每次增加一倍。m>n-1时的结果与n-1时的结果相同，最终的时间复杂度被压缩到O(n^3 lgn)。(详见具体代码)

具体代码：

import java.util.Scanner;
/**
 * 
 * @author Founder
 *
 */
public class Main{
   
    private static final int INFINITE = 1000000000;
    public static void main(String[] args){
        int[][] matrix = initialize();
        print(getPairsPath(matrix));
    }

    public static int[][] initialize(){
        Scanner input = new Scanner(System.in);
        int n = input.nextInt();
        int[][] data = new int[n][n];
        for(int i = 0; i < n; ++i)
            for(int j = 0; j < n; ++j)
                data[i][j] = input.nextInt();
        return data;
    }

    public static int[][] extendPath(int[][] matrix){
        int[][] newMatrix = new int[matrix.length][matrix.length];
        for(int i = 0; i < matrix.length; ++i)
            for(int j = 0; j < matrix.length; ++j){
                newMatrix[i][j] = INFINITE;
                for(int k = 0; k < matrix.length; ++k)
                    if(matrix[i][k] + matrix[k][j] < newMatrix[i][j]){
                        newMatrix[i][j] = matrix[i][k] + matrix[k][j];
                    }
            }
        return newMatrix;
    }

    public static int[][] getPairsPath(int[][] matrix){
        int m = matrix.length;
        int i = 1;//i代表路径边数
        while(i < m - 1){
            matrix = extendPath(matrix);
            m *= 2;
        }
        return matrix;
    }

    public static void print(int[][] matrix){

        for(int i = 0; i < matrix.length; ++i)
            for(int j = 0; j < matrix.length; ++j){
                if(matrix[i][j] != INFINITE && i != j){
                    System.out.println("From " + i + " to " + j + " the cost is:" + matrix[i][j]);
                }
            }
    }

}

测试用例：

输入：

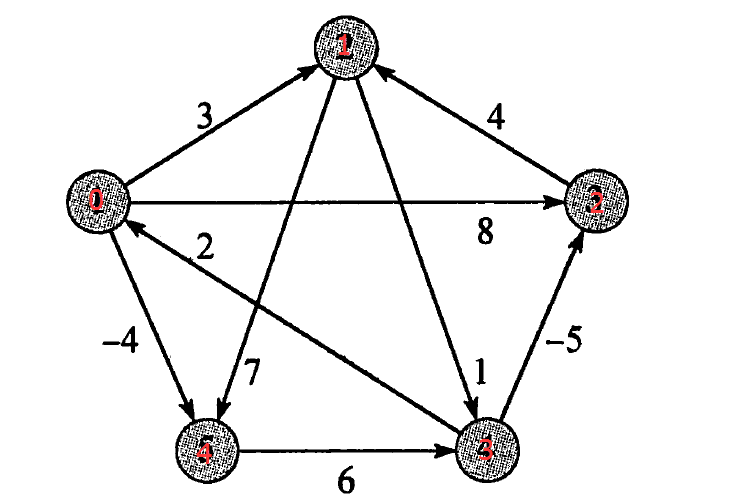
5
0 3 8 1000000000 -4
1000000000 0 1000000000 1 7
1000000000 4 0 1000000000 1000000000
2 1000000000 -5 0 1000000000
1000000000 1000000000 1000000000 6 0

输出：

From 0 to 1 the cost is:1
From 0 to 2 the cost is:-3
From 0 to 3 the cost is:2
From 0 to 4 the cost is:-4
From 1 to 0 the cost is:3
From 1 to 2 the cost is:-4
From 1 to 3 the cost is:1
From 1 to 4 the cost is:-1
From 2 to 0 the cost is:7
From 2 to 1 the cost is:4
From 2 to 3 the cost is:5
From 2 to 4 the cost is:3
From 3 to 0 the cost is:2
From 3 to 1 the cost is:-1
From 3 to 2 the cost is:-5
From 3 to 4 the cost is:-2
From 4 to 0 the cost is:8
From 4