从零学习Belief Propagation算法（二）

从零学习Belief Propagation算法（二）

本文将记录 Belief Propagation 算法的学习历程，如果您之前没有接触过，而现在刚好需要用到，可以参考我的系列文章。内容稍多将分为几个主题来写。本系列文章将包含以下内容：

• 必备的概率论基础
• 从概率论到概率图模型
• Bayes 网络
• Markov 随机场
• 因子图 Factor Graph
• Belief Propagation算法

---

从零学习Belief Propagation算法（一）

---

1. 贝叶斯网络

1.1 概念

贝叶斯网络(Bayesian Network)，又称信念网络(Belief Network)，或称有向无环图模型(directed acyclic graphical model，DAG)。它和MRF是深度学习中 RBM、DBM 的基础。

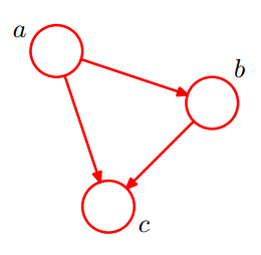
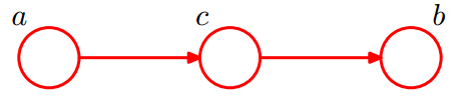
上图是一个简单的贝叶斯网络，它的随机变量是 $a,b,c$，其联合概率可以根据箭头的指向如此表示：
$$P(a,b,c)=P(a)P(b|a)P(c|a,b)$$
从图中可以得知三个随机变量之间都有箭头，说梦彼此有联系，存在条件概率，所以不存在独立的变量。

1.2 条件独立

这块内容和 BP 算法的推导关系不是很大，所以你要是赶时间，可以跳过这一小节。但是这一小节和理解马尔科夫链至关重要，所以可以为了兴趣和博学稍微看看。

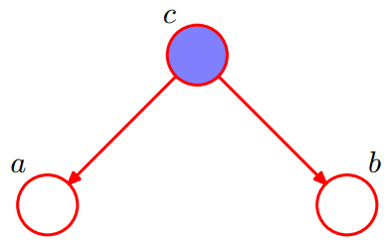
• 条件独立【1】：tail-to-tail
  

考虑c的两种情况：

• 在 $c$ 未知时，有：$P(a,b,c)=P(c)\ast P(a|c)\ast P(b|c)$，此时得不到$P(a,b)=P(a)P(b)$，即 $c$ 未知时，$a、b$ 不独立。
• 在 $c$ 已知时，有：
  $$\begin{gathered} P(a,b|c)=\frac{P(a,b,c)}{P(c)}=\frac{P(c)\ast P(a|c)\ast P(b|c)}{P(c)} \\ =P(a|c)\ast P(b|c)=P(a,b|c) \end{gathered}$$即 $c$ 已知时，$a、b$ 条件独立。

所以，在 $c$ 被给定的条件下，$a、b$ 被阻断(blocked)而条件独立，称之为tail-to-tail条件独立。

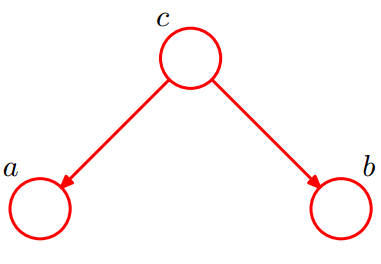
• 条件独立【2】：head-to-head

$$\begin{gathered} P(a,b,c)=P(a)\ast P(b)\ast P(c|a,b) \\ =P(a,b)\ast P(c|a,b) \end{gathered}$$
可以得到：
$$P(a,b)=P(a)\ast P(b)$$

即在 $c$ 没有给定的条件下，$a、b$ 被阻断(blocked)而独立，称为head-to-head条件独立。

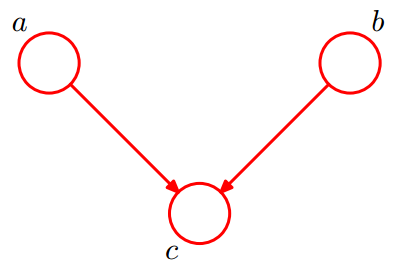
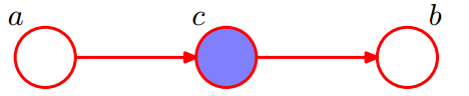
• 条件独立【3】：head-to-tail

像分析第一类条件独立一样，考虑 $c$ 的两种情况：

• 未知 $c$ 时，有：$P(a,b,c)=P(a)\ast P(c|a)\ast P(b|c)$，无法推出$P(a,b)=P(a)P(b)$，即 $c$ 未知时，$a、b$不独立。

• 已知 $c$ 时，有：
  $$\begin{gathered} P(a,b|c)=\frac{P(a,b,c)}{P(c)} \\ =\frac{P(a)\ast P(c|a)\ast P(b|c)}{P(c)} \\ =\frac{P(c)\ast P(a|c)\ast P(b|c)}{P(c)} \\ =P(a|c)\ast P(b|c) \end{gathered}$$

所以在给定 $c$ 的条件下，$a、b$被阻断(blocked)而独立，称为head-to-tail条件独立。

---

如果是这么一个结构：

我们已经知道，在 $X_i$ 给定的条件下，$X_{i+1}$ 的分布和 $X1,X2\dots X_{i-1}$ 条件独立。这就意味着：$X_{i+1}$ 的分布状态只和 $X_i$ 有关，和其他变量条件独立。
通俗点说，当前状态只跟上一状态有关，跟上上或上上之前的状态无关。这种顺次演变的随机过程，叫做马尔科夫链（Markov chain）。

$$P(X_{i+1}=x|X1,X2\dots X_i)=P(X_{i+1}=x|X_i)$$

---

2. 马尔科夫随机场（MRF）

• 前面看了概率有向图模型，必然对无向图模型也要研究一下。它不仅和 BP 算法的因子图有关，而且这个概率无向图模型对学习 RBM 有很大的帮助，它关系到能量函数的来源。

• 它虽然比较重要，但是里面涉及到了一些物理的知识，我们只需要了解会应用，不必深究。而且这块只需要大概了解，如果你看着比较吃力，可以选择跳过这部分当中较难的一些点，直接来看后面的因子图。

• 有向图（Bayesian Networks）将一组变量上的联合分布分解为多个局部条件概率分布的乘积；同时定义了一组条件独立的性质，根据图进行分解的任何概率分布都必须满足这些条件独立性质（三种拓扑结构）。

• 同理，无向图也是一种分解方式。

---

2.1 概念

概率无向图模型（undirect graphical model），又叫做马尔科夫随机场（Markov Random Filed，MRF），或称马尔科夫网络（Markov Network，MN）。

怎么理解呢？前面的有向图代表的是变量之间的关系很明确，比如A,B接力赛，A跑的时间绝对是决定了B的时间，这样A和B之间就有了明确的条件概率关系，而且关系方向很确定。

无向图描述的也是变量之间的关系，但这种关系很模糊，没有方向。我买可以这么理解：A、B两个人是同学，A感冒传染给B也可以，B传染给A也可以，箭头方向是不是就可以取消了。

---

2.2 结构、条件独立

• 包含⼀组结点。
• 每个结点都对应着⼀个变量。
• 链接是⽆向的，即不含有箭头。

在无向图的情形中，讨论条件独立性质是比较方便的。

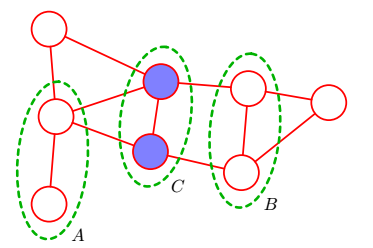
考虑连接集合 A 和 B 的节点的所有可能路径，如果所有路径都通过集合 C 中一个或者多个节点，那么所有这样的路径都被“阻隔”，条件独立性质成立；
如果存在至少一条未被阻隔的路径，那么条件独立性质就未必成立。

更为显然的检测方法是，将图中属于集合 C 的节点以及与这些节点相连的连接线全部删除，然后再看有没有从 A 到 B 的路径。如果没有，那么条件独立一定成立。

---

2.3 联合概率分解

在了解联合概率分布的写法之前先了解两个概念：

• 团块：图中结点的子集，子集的节点之间一定两两直接连接（间接连接起来的不算）。团块中的节点集合是全连接的。

• 最大团块：将图中任何一个其它节点接到该到团块中就会破坏团块的性质（不再两两连接）。

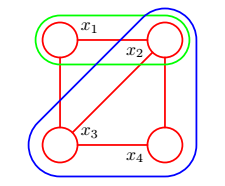
上图中有很多团块，我们举几个例子（其他请您自己穷举）：绿色部分{$x_1$，$x_2$}；蓝色部分{$x_2$，$x_3$，$x_4$}

接下来我们可以顺利讨论怎么分解因子写出来联合概率了，但是由于公式看着理解比较棘手，我们先看一个具体的例子算式，这样有助于我们理解公式：

此图中包含三个极大团块：集合 $C_1$={$x_1,x_2,x_3$}、$C_2$={$x_3,x_4$}、$C_3$={$x_3,x_5$}；

那么此马尔科夫网络的联合概率分布可以写为：

$$P(x_1,x_2\dots x_5)=\frac{1}{Z}{\psi }_{C_1}(x_1,x_2,x_3){\psi }_{C_2}(x_3,x_4){\psi }_{C_3}(x_3,x_5)$$

在这里，我们需要简单解释一下 势函数 ${\psi }_{C_i}(x_i)$：
$${\psi }_{C_1}(x_1,x_2,x_3)=e^{-E(x_1,x_2,x_3)}$$
可以看到势函数严格为正，其中 Z 是归一化用的（配分函数 )，加和消去了所有变量。（有一定难度，想深入了解可自行查阅资料）
$$Z=\sum _x\prod _C{\psi }_C(x_C)$$
E 被称为能量函数(energy function)，指数表示被称为玻尔兹曼分布（Boltzmann distribution）。联合概率分布被定义为势函数的乘积。

重写标准的联合分布：

$$P(\text{x})=\frac{1}{Z}\prod _C{\psi }_C(x_C)$$

重写理解马尔可夫随机场（Markov Random Field）：它包含两层意思：一是什么是马尔可夫，二是什么是随机场。

• 马尔可夫性质的简称。它指的是一个随机变量序列按时间先后关系依次排开的时候，**第 t+1 时刻的分布特性，与 t 时刻以前的随机变量的取值无关。**比如我们假定天气是马尔可夫的，意思就是我们假设今天的天气仅仅与昨天的天气存在概率上的关联，而与前天及前天以前的天气没有关系。

• 随机场包含两个要素：位置（site），相空间（phase space）。当给每一个位置中按照某种分布随机赋予相空间的一个值之后，其全体就叫做随机场。我们不妨拿种地来打个比方：“位置”好比是一亩亩农田；“相空间”好比是种的各种庄稼。我们可以给不同的地种上不同的庄稼，这就好比给随机场的每个“位置”，赋予相空间里不同的值。所以通俗说，随机场就是在哪块地里种什么庄稼的事情。
• 好了，明白了上面两点，就可以讲马尔可夫随机场了。还是拿种地打比方：如果任何一块地里种的庄稼的种类，仅仅与它邻近的地里种的庄稼的种类有关，与其它地方的庄稼的种类无关，那么这些地里种的庄稼的集合，就是一个马尔可夫随机场。

---

参考文献

[1] : http://blog.csdn.net/aspirinvagrant/article/details/40862237
[2] : http://blog.csdn.net/v_july_v/article/details/40984699
[3] : http://blog.csdn.net/zb1165048017/article/details/60867140
[4] : http://blog.csdn.net/xyzariel/article/details/44858833