从一元高斯分布到多元高斯分布（含例子，python代码）

最新推荐文章于 2024-05-22 22:03:22 发布

妖白

最新推荐文章于 2024-05-22 22:03:22 发布

阅读量1.5w

点赞数 5

分类专栏：数学知识

数学知识专栏收录该内容

5 篇文章 1 订阅

订阅专栏

为了简化下面的高斯分布都是按照零均值写的

一元高斯的标准形式： $p(x) = \frac{1}{\sqrt{2\pi}}\exp(-\frac{1}{2}x^2)$

多元高斯的标准形式： $p(\mathbf{x}) = \prod_{i=1}^n\frac{1}{\sqrt{2\pi}}\exp(-\frac{1}{2}x_i^2) = \frac{1}{(2\pi)^{\frac{n}{2}}} \exp(-\frac{1}{2}\mathbf{x^TIx})$

下面推导为什么一般的多元高斯具有形式： $p(\mathbf{x}) = \frac{1}{(2\pi)^{\frac{n}{2}}|\Sigma|^{\frac{1}{2}}}\exp(-\frac{1}{2}\mathbf{x^T\Sigma^{-1}x})$

核心观点：所有的非奇异的多元高斯分布都是以多元标准高斯分布为基础，通过非奇异矩阵 $A$ 进行坐标变换而来的

假设对于一般的多元高斯分布 $p(\mathbf{y})$ 有 $\mathbf{y=Ax, x = A^{-1}y}$

那么

$\begin{align} &p(\mathbf{y}) = p(\mathbf{x})|\frac{dx}{dy}| \\ &= \frac{1}{(2\pi)^{\frac{n}{2}}} \exp\{-\frac{1}{2}\mathbf{(A^{-1}y)^TI(A^{-1}y)}\} |\frac{dx}{dy}|\\ &= \frac{1}{(2\pi)^{\frac{n}{2}}|A|} \exp\{-\frac{1}{2}\mathbf{y^T(AA^T)^{-1}y}\} \end{align}$

$\Sigma_y = \mathbb{E}[yy^T] = A\mathbb{E}[xx^T]A^T= AA^T$

因此 $p(\mathbf{y}) = \frac{1}{(2\pi)^{\frac{n}{2}}|\Sigma|^{\frac{1}{2}}} \exp\{-\frac{1}{2}\mathbf{y^T\Sigma^{-1}y}\}$

这样应该就可以理解公式里面为什么会有协方差矩阵了

代码示例

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

以二维高斯为例

plt.figure(dpi=120)
plt.axis([-4,4,-4,4])  
plt.gca().set_aspect(1)
X = np.random.multivariate_normal(mean=[0,0], cov=[[1, 0], [0,1]], size = 1000)
plt.scatter(X[:,0], X[:,1])

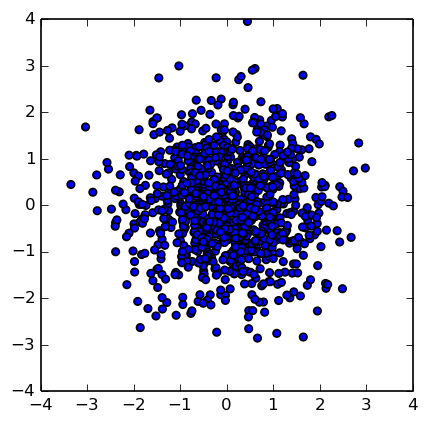&lt;img src="https://pic1.zhimg.com/50/v2-73639854084ec72a3d421ebb308b683f_hd.jpg" data-size="normal" data-rawwidth="429" data-rawheight="425" class="origin_image zh-lightbox-thumb" width="429" data-original="https://pic1.zhimg.com/v2-73639854084ec72a3d421ebb308b683f_r.jpg"&gt; 标准分布

数据变换

A = np.array([[1,2],[2,1]])
Y = X.dot(A)

plt.figure(dpi=120)
plt.axis([-6,6,-6,6])  
plt.gca().set_aspect(1)
plt.scatter(Y[:,0], Y[:,1])

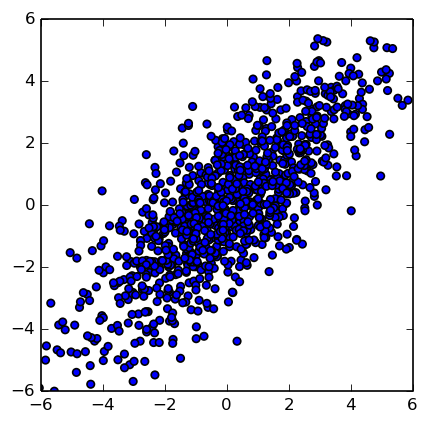&lt;img src="https://pic3.zhimg.com/50/v2-83d2ceb4e37bcc41f8ae86b746f15a1c_hd.jpg" data-size="normal" data-rawwidth="428" data-rawheight="425" class="origin_image zh-lightbox-thumb" width="428" data-original="https://pic3.zhimg.com/v2-83d2ceb4e37bcc41f8ae86b746f15a1c_r.jpg"&gt; 变化后分布

验证

print(Y.transpose().dot(Y) / 1000)
# array([[ 4.84023848,  3.92638569],
#        [ 3.92638569,  5.01025796]])
print(A.dot(A.transpose()))
# array([[5, 4],
#        [4, 5]])

可以看出转化后的数据Y的协方差 $\Sigma = AA^T$

作者：Hao Zen
链接：https://www.zhihu.com/question/21024811/answer/228812435
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

一个例子：http://caifuhao.eastmoney.com/news/20171018074421442120410

还是对计算机的监测，我们发现CPU负载和占用内存之间，存在正相关关系。

CPU负负载增加的时候占用内存也会增加：

假如我们有一个数据，x1 的值是在 0.4 和 0.6 之间，x2 的值是在 1.6 和 1.8 之间，就是下图中的绿点：

它明显偏离了正常的范围，所以是一个异常的数据。

但如果单独从CPU负载和占用内存的角度来看，该数据却是混杂正常数据之中，处于正常的范围：

这个异常的数据会被认为是正常的，因为我们得到模型的轮廓图是这样的：

为了改良这样的情况，我们需要把特征之间的相关性考虑进来。

第一种方式我们在上一篇笔记中有提到，就是增加一个新的特征 x3 ，把两者的相关性考虑进去：

另外一种方式就是形成多元高斯分布（Multivariate Gaussian Distribution），自动捕捉特征之间的相关性，公式如下：

其中 μ 为特征的均值，是一个 n � 1 的向量：

Σ 为特征的协方差，是一个 n � n 的矩阵：

假设我们的均值与协方差的初始值和对应的三维图形与轮廓图如下：

μ 决定的是中心的位置，改变 μ 的值意味着中心的移动：

协方差矩阵控制的是对概率密度的敏感度。

例如某个方向的协方差越小，那么随着在该方向上的水平位移，高度的变化就越大。

首先我们看看各个特征不相关（正交）的情况：

我们再看一下考虑特征相关性的情况，下面两个图片分别到正相关和负相关的变化：

你看之前的模型 p(x) 会把异常数据认定为正常，而到了多元高斯分布的模型中，就得到了很好的解决：

之前的模型：

其实是多元高斯分布的一种特例，就是协方差矩阵 Σ 为对角矩阵的情况：

进行一个简单的推演你就明白了。

假设我们只有两个特征：

那么均值和协方差矩阵分别是：

把它们代入到多元高斯分布的公式中，可以推演得到：

二元高斯分布的密度函数，其实就是两个独立的高斯分部密度的乘积，特征更多的情况也是类似的。

需要注意的是，这里的推导不是证明的过程，仅仅是为了让你更好地理解两者的关系。

我们知道有这么两种方式可以处理特征之间的相关关系，那么应该如何选择呢？

这个需要根据具体的现实条件进行选择。

下表是两者的对比：

原来的模型多元高斯分布手工创建新特征来捕捉特征的相关性自动捕捉特征的相关性运算量要求不高需要求协方差矩阵的逆矩阵，对运算量要求较高对训练集数量 m 的要求不高，即使数量很小也可以正常运行求协方差逆矩阵要求训练数量 m大于特征数量 n

妖白

关注

5
点赞
踩
52

收藏

觉得还不错? 一键收藏
0
评论
从一元高斯分布到多元高斯分布（含例子，python代码）

为了简化下面的高斯分布都是按照零均值写的一元高斯的标准形式：多元高斯的标准形式：下面推导为什么一般的多元高斯具有形式：核心观点：所有的非奇异的多元高斯分布都是以多元标准高斯分布为基础，通过非奇异矩阵进行坐标变换而来的假设对于一般的多元高斯分布有那么因此这样应该就可以理解公式里面为什么会有协方差矩阵了代码示例import numpy as npimport matplotlib....
复制链接

扫一扫