数据结构基础— Tree Traversals Again

我觉得这道题真的是树的递归的应用的超级好的例题，把二叉树的遍历的递归性的举一反三的能力考察的淋漓尽致。

从输入的push pop可以看出来就是给出了前序和中序，输出是后序遍历：

前序就是每次push时候的输出：1 2 3 4 5 6；   中序就根据pop的顺序：3 2 4 1 6 5; 再确定一下整棵树的根节点就是 push 的第一棵树 1；然后把先序的遍历值储存在preorder[30]中，把中序的遍历值储存在inorder[30]中，然后再调用makeMyTree函数。

递归调用makeMyTree函数的话，那么总的思路就是：递归左子树 + 递归右子树 + 输入根节点。是不是很像后序输出？我们的任务就是找到树的根节点。

 我一直觉得其实每一个节点都是一个子树，比如叶节点，两个子树都是NULL，那么这个节点就是这个子树的根，这和用堆栈进行后续遍历是同样的道理, (如果把叶节点看成一棵树的话，第一次访问：入栈； 第二次访问，左节点为NULL，返回； 第三次访问，右节点为NULL，返回。而且实际上得归也是这么做的），在这里就用length == 0来做判断.

03-树3 Tree Traversals Again（25 分）

An inorder binary tree traversal can be implemented in a non-recursive way with a stack. For example, suppose that when a 6-node binary tree (with the keys numbered from 1 to 6) is traversed, the stack operations are: push(1); push(2); push(3); pop(); pop(); push(4); pop(); pop(); push(5); push(6); pop(); pop(). Then a unique binary tree (shown in Figure 1) can be generated from this sequence of operations. Your task is to give the postorder traversal sequence of this tree.

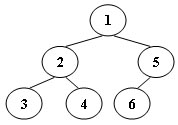
Figure 1 

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer $N$ ($\le 30$) which is the total number of nodes in a tree (and hence the nodes are numbered from 1 to $N$). Then $2N$ lines follow, each describes a stack operation in the format: "Push X" where X is the index of the node being pushed onto the stack; or "Pop" meaning to pop one node from the stack.

Output Specification:

For each test case, print the postorder traversal sequence of the corresponding tree in one line. A solution is guaranteed to exist. All the numbers must be separated by exactly one space, and there must be no extra space at the end of the line.

Sample Input:

6
Push 1
Push 2
Push 3
Pop
Pop
Push 4
Pop
Pop
Push 5
Push 6
Pop
Pop

Sample Output:

3 4 2 6 5 1

先看关于指针参数传递的一些测试

#include <stdio.h>
void test1(int a[]);
void test2(int *a);
int main(int argc, const char * argv[]) {
    int a[5] = {1,2,3,4,5};
    test1(a);
    test2(a);
}
void test1(int a[]){
    printf("%p\n",a);      //address 0x7fff5fbff6b0
    printf("%p\n",a+1);    //address 0x7fff5fbff6b4 地址加了4位
    printf("%d\n",a[0]);   //number of a[0]
}
void test2(int *a){
    printf("%p\n",a);    //address 0x7fff5fbff6b0
    printf("%p\n",a+1);  //address 0x7fff5fbff6b4
    printf("%d\n",*a);    //number of a[0] 相当于解义
    printf("%d\n",a[0]);   //number of a[0]
}

然后这道题的代码：

#include <stdio.h>

int root; /*建这个变量是为了奇葩的输出格式*/
void makeMyTree(int *preorder, int *inorder, int length);
int main(int argc, const char * argv[]) {
    char st[4];/*store push or pop*/
    int length,tmpindex = 0,preindex = 0,inindex = 0;
    int preorder[30];
    int inorder[30];
    int tmp[30];
    scanf("%d",&length);
    
    /* 初始化数组 */
    for(int i = 0; i < 30; i++){
        preorder[i] = 0;
        inorder[i] = 0;
        tmp[i] = 0;
    }
    /* 读入前序和中序的顺序 */
    for (int i = 0; i < 2*length; i++) {
         scanf("%s",&st);
        if(st[1] == 'u'){/* 如果输入的是push */
            scanf("%d",&preorder[preindex]);
            tmp[tmpindex] = preorder[preindex];
            preindex ++;
            tmpindex ++;
        }else{ /* 如果输入的是pop */
            inorder[inindex++] = tmp[--tmpindex];
        }
    }
    root = preorder[0]; /* 确定根节点*/
    makeMyTree(preorder, inorder,length);
    return 0;
}

/* preorder[] is the address */
void makeMyTree(int *preorder, int *inorder, int length){
    if(length == 0) return;
    int number = *preorder; /*储存当前子树的根节点*/
    int rootindex;
    for(rootindex = 0; rootindex < length; rootindex ++){
        if(inorder[rootindex] == *preorder)
            break;
    }
    makeMyTree(preorder + 1, inorder, rootindex); /*递归左子树*/
    makeMyTree(preorder + rootindex +1, inorder + rootindex + 1, length-(rootindex+1));/*递归右子树*/
    if(number != root)
        printf("%d ",number);
    else
        printf("%d",number);
    return;
}