codeforces917b(dp)

B. MADMAX

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

As we all know, Max is the best video game player among her friends. Her friends were so jealous of hers, that they created an actual game just to prove that she's not the best at games. The game is played on a directed acyclic graph (a DAG) with n vertices and medges. There's a character written on each edge, a lowercase English letter.

Max and Lucas are playing the game. Max goes first, then Lucas, then Max again and so on. Each player has a marble, initially located at some vertex. Each player in his/her turn should move his/her marble along some edge (a player can move the marble from vertex v to vertex u if there's an outgoing edge from v to u). If the player moves his/her marble from vertex v to vertex u, the "character" of that round is the character written on the edge from v to u. There's one additional rule; the ASCII code of character of round i should begreater than or equal to the ASCII code of character of round i - 1 (for i > 1). The rounds are numbered for both players together, i. e. Max goes in odd numbers, Lucas goes in even numbers. The player that can't make a move loses the game. The marbles may be at the same vertex at the same time.

Since the game could take a while and Lucas and Max have to focus on finding Dart, they don't have time to play. So they asked you, if they both play optimally, who wins the game?

You have to determine the winner of the game for all initial positions of the marbles.

Input

The first line of input contains two integers n and m (2 ≤ n ≤ 100, ).

The next m lines contain the edges. Each line contains two integers v, u and a lowercase English letter c, meaning there's an edge from vto u written c on it (1 ≤ v, u ≤ n, v ≠ u). There's at most one edge between any pair of vertices. It is guaranteed that the graph is acyclic.

Output

Print n lines, a string of length n in each one. The j-th character in i-th line should be 'A' if Max will win the game in case her marble is initially at vertex i and Lucas's marble is initially at vertex j, and 'B' otherwise.

Examples

input

4 4
1 2 b
1 3 a
2 4 c
3 4 b

output

BAAA
ABAA
BBBA
BBBB

input

5 8
5 3 h
1 2 c
3 1 c
3 2 r
5 1 r
4 3 z
5 4 r
5 2 h

output

BABBB
BBBBB
AABBB
AAABA
AAAAB

Note

Here's the graph in the first sample test case:

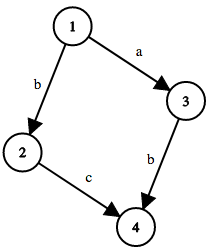
Here's the graph in the second sample test case:

题意：给出一个有向无环图，每条边都有权值，两个人在图中轮流走一步，每个人走的边的权值必须大于等于上一个人走的边的权值，一个人无法走的时候就输了，输出所有情况的胜负情况。

思路：dp[i][j][k]代表先手在i节点，后手在j节点，上一回合所走边的权值为k时，先手的胜负情况。那么令to代表i所通向的节点，ch代表i到to的边权大小。那么dp[i][j][k]的值就依赖于所有ch大于k的dp[j][to][ch]，代表先手从i到to走了一步后的后手胜负情况。如果存在to使得 dp[j][to][ch]为必败态，那么dp[i][j][k]为必胜态。

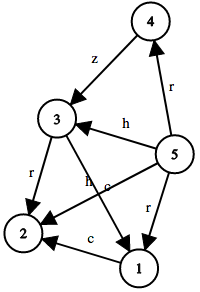
#include<iostream>
#include<stdio.h>
#include<string.h>
#include<vector>
using namespace std;
int map[105][105];
int n,m;
int dp[105][105][26];
vector<int>g[105];
int dfs(int x,int y,int ch)
{
	if(dp[x][y][ch]>0)return dp[x][y][ch];
	for(int i=0;i<g[x].size();i++)
	{
		int to=g[x][i];
		if(map[x][to]>=ch&&dfs(y,to,map[x][to])==0)
		{
			return dp[x][y][ch]=1;
		}
	}
	return dp[x][y][ch]=0;
}
int main()
{
	
	while(~scanf("%d%d",&n,&m))
	{
		memset(map,0,sizeof(map));
		for(int i=0;i<105;i++)g[i].clear();
		int u,v;
		char s[5];
		for(int i=0;i<m;i++)
		{
			scanf("%d%d%s",&u,&v,s);
			map[u][v]=s[0]-'a';
			g[u].push_back(v);
		}
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=n;j++)
			{
				dfs(i,j,0);  //先手在i，后手在j出发 
			}
		}
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=n;j++)
			{
				if(dp[i][j][0])printf("A");
				else printf("B");
			}
			printf("\n");
		}
	}
}