回朔法简单总结

（尊重劳动成果，转载请注明出处：http://blog.csdn.net/qq_25827845/article/details/77197782冷血之心的博客）

回溯法（探索与回溯法）是一种选优搜索法，又称为试探法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。

在回溯法中，每次扩大当前部分解时，都面临一个可选的状态集合，新的部分解就通过在该集合中选择构造而成。这样的状态集合，其结构是一棵多叉树，每个树结点代表一个可能的部分解，它的儿子是在它的基础上生成的其他部分解。树根为初始状态，这样的状态集合称为状态空间树。

回溯法解题的关键要素：
确定了问题的解空间结构后，回溯法将从开始结点(根结点)出发，以深度优先的方式搜索整个解空间。开始结点成为活结点，同时也成为扩展结点。在当前的扩展结点处，向纵深方向搜索并移至一个新结点，这个新结点就成为一个新的活结点，并成为当前的扩展结点。如果在当前的扩展结点处不能再向纵深方向移动，则当前的扩展结点就成为死结点。此时应往回移动(回溯)至最近的一个活结点处，并使其成为当前的扩展结点。回溯法以上述工作方式递归地在解空间中搜索，直至找到所要求的解或解空间中已无活结点时为止。
运用回溯法解题的关键要素有以下三点：
(1) 针对给定的问题，定义问题的解空间；
(2) 确定易于搜索的解空间结构；
(3) 以深度优先方式搜索解空间，并且在搜索过程中用剪枝函数避免无效搜索。

我们来看一下递归实现回朔法的模板代码：

void BackTrace(int t) {
		if (t > n)
			Output(x);
		else
			for (int i = f(n, t); i <= g(n, t); i++) {
				x[t] = h(i);
				if (Constraint(t) && Bound(t))
					BackTrace(t + 1);
			}
	}

下边看几个LeetCode上几道典型的回朔法：

题目一：

题目的大意就是按照手机键盘上，每个数字可以表示的意义，给定一个字符串数字，列举出所有可能的字符组合~

结题思路：使用递归模板搞定

public class Solution {
    List<String> list = new ArrayList<String>();
    String[] letterMap = {
        " ", // 0
        "",  // 1
        "abc",
        "def",
        "ghi",
        "jkl",
        "mno",
        "pqrs",
        "tuv",
        "wxyz"
    };
    public List<String> letterCombinations(String digits) {
        if(digits==null||digits.equals(""))
            return list;
        
        generate(digits,0,"");
        
        return list;
    }
    private void generate(String digits,int index,String s){
        // 此时s是其中的一个解
        if(index==digits.length()){
            list.add(s);
            return ;
        }
        char c = digits.charAt(index);
        if(c>='0'&&c<='9'&&c!='1'){
            String letters = letterMap[c-'0'];
            for(int i = 0;i<letters.length();i++){
                generate(digits,index+1,s+letters.charAt(i));
            }
        }
        
    }
}

题目二：求全排列

题目大意就是给定一个数组，求其全排列组合

public class Solution {
    List<List<Integer>> res = new ArrayList<List<Integer>>();
    public List<List<Integer>> permute(int[] nums) {
        List<Integer> list = new ArrayList<Integer>();
        if(null==nums||nums.length==0)
            return res;
        get1Result(nums,0,list);
        return res;
    }
    // list中保存了一个有index个元素的排列
    // 向这个排列的末尾添加第index+1个元素，获得一个有index+1个元素的排列
    private void get1Result(int[] nums,int index,List<Integer> list){
        if(index==nums.length){
            res.add(new ArrayList<Integer>(list));
            return ;
        }
        for(int i = 0;i<nums.length;i++){
            if(!list.contains(nums[i])){
                list.add(nums[i]);
                get1Result(nums,index+1,list);
                list.remove(list.size()-1);
            }
        }
            
    }
}

题目三：求所有组合

题目大意就是说从n个数中取出k个数，找出所有的组合，利用递归模板代码，我们可以得出以下的代码：

public class Solution {
    List<List<Integer>> res = new ArrayList<List<Integer>>();
    public List<List<Integer>> combine(int n, int k) {
        if(n<=0||k<=0||k>n)
            return res;
        List<Integer> list = new ArrayList<Integer>();
        generateCombine(n,k,1,list);
        return res;
    }
    
    // 求解C（n,k），当前已经找到的组合存储在c中，需要从start开始搜索新的元素
    private void generateCombine(int n,int k,int start ,List<Integer> list){
        if(list.size()==k){  // 递归结束条件
            res.add(new ArrayList<Integer>(list));
            return ;
        }
        // 递归过程
         for(int i = start;i<=n;i++){
            list.add(i);
            generateCombine(n,k,i+1,list);
            list.remove(list.size()-1);
        }
    }
}

运行结果如下：用了25ms。

这个时候就涉及到了一种回溯剪枝的问题，我们还是依照例子中的n = 4, k = 2来说明，有如下的树形图：

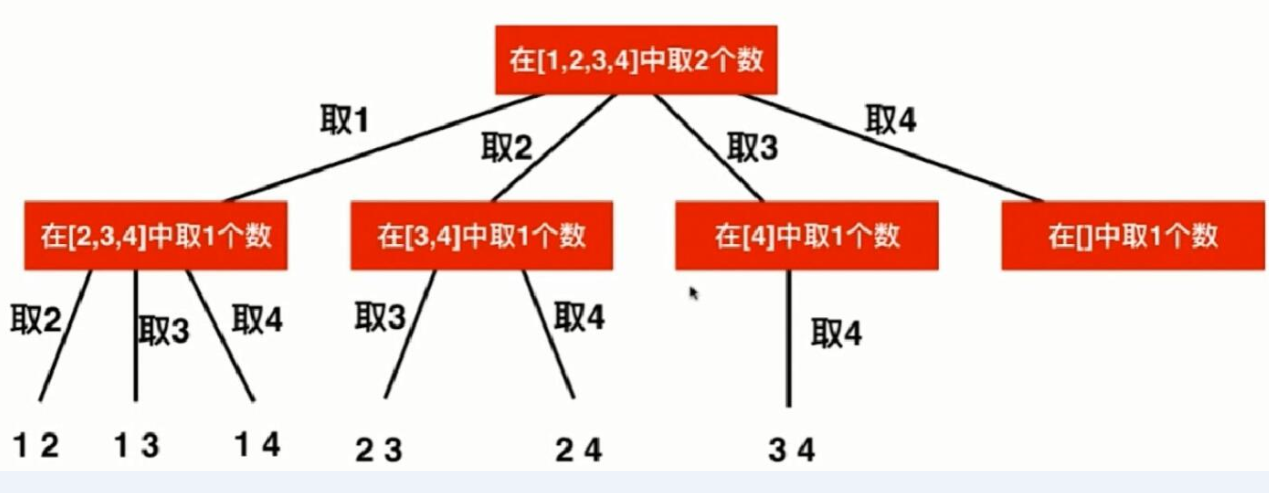
也就是说，我们可以在递归过程中，将不必要的枝条从树中减掉，比如说本例中的取4！！！

剪枝之后的代码如下：

public class Solution {
    List<List<Integer>> res = new ArrayList<List<Integer>>();
    public List<List<Integer>> combine(int n, int k) {
        if(n<=0||k<=0||k>n)
            return res;
        List<Integer> list = new ArrayList<Integer>();
        generateCombine(n,k,1,list);
        return res;
    }
    
    // 求解C（n,k），当前已经找到的组合存储在c中，需要从start开始搜索新的元素
    private void generateCombine(int n,int k,int start ,List<Integer> list){
        if(list.size()==k){
            res.add(new ArrayList<Integer>(list));
            return ;
        }
        // 递归过程
        // 还有k-list.size()个空位，所以，[i...n]中至少要有k-list.size()个元素
        // i最多为n-(k-list.size())+1，否则没有那么多元素可以放入list中了。
        for(int i = start;i<=n-(k-list.size())+1;i++){
            list.add(i);
            generateCombine(n,k,i+1,list);
            list.remove(list.size()-1);
        }
    }
}

运行结果如下：仅仅只用了4ms，也就是说少用了21ms，简直就是完美的提升~

总结：

针对递归实现的回溯法，我们的基本思路是，首先定义一个用于递归的函数，在主函数中调用该递归函数；然后在递归函数中先判断是否达到了递归结束条件，之后进行循环遍历，在循环过程中，依次进行递归操作，设计到list的操作，主要要remove进行回退；最后，如果可以的话，记得注意剪枝操作，可以大大提升运行效率哦~

以上就是关于递归实现回溯法的简单学习，如果对你有帮助，记得点赞哦~欢迎大家关注我的博客，可以进群366533258一起交流学习哦~

本群给大家提供一个学习交流的平台，内设菜鸟Java管理员一枚、精通算法的金牌讲师一枚、Android管理员一枚、蓝牙BlueTooth管理员一枚、Web前端管理一枚以及C#管理一枚。欢迎大家进来交流技术。