最大子段和问题

  最大子段和的问题相信大家遇到了很多次，碰巧今日我想到了时间复杂度，就在考虑什么情况下可以考虑什么方案呢？

相信最普遍的暴力大家是知道的，今天我们一起来讨论下这个问题吧！

方案一：暴力，可行性❤

最简单的方法当然是最简单粗暴的啦，三层枚举，时间复杂度为O（n^3）。

可行性范围：n<=100

#include <iostream>
using namespace std;
#define N 101
int node[N];
int main()
{
    int n;
    while(cin>>n)
    {
        int i;
        for(i=1;i<=n;i++)
            cin>>node[i];
        //三层暴力求最大和
        int maxsum=0,tmpsum=0;
        int from=0,to=0;
        int j,k;
        for(i=1;i<=n;i++)
        {
            for(j=i;j<=n;j++)
            {
                tmpsum=0;
                for(k=i;k<=j;k++)//求node[i]到node[j]的和
                {
                    tmpsum+=node[k];
                }
                if(tmpsum>maxsum)
                {
                    maxsum=tmpsum;
                    from=i;
                    to=j;
                }
            }
        }
        cout<<"From="<<from<<",To="<<to<<endl;
        cout<<"MaxSum="<<maxsum<<endl;
    }
    return 0;
}

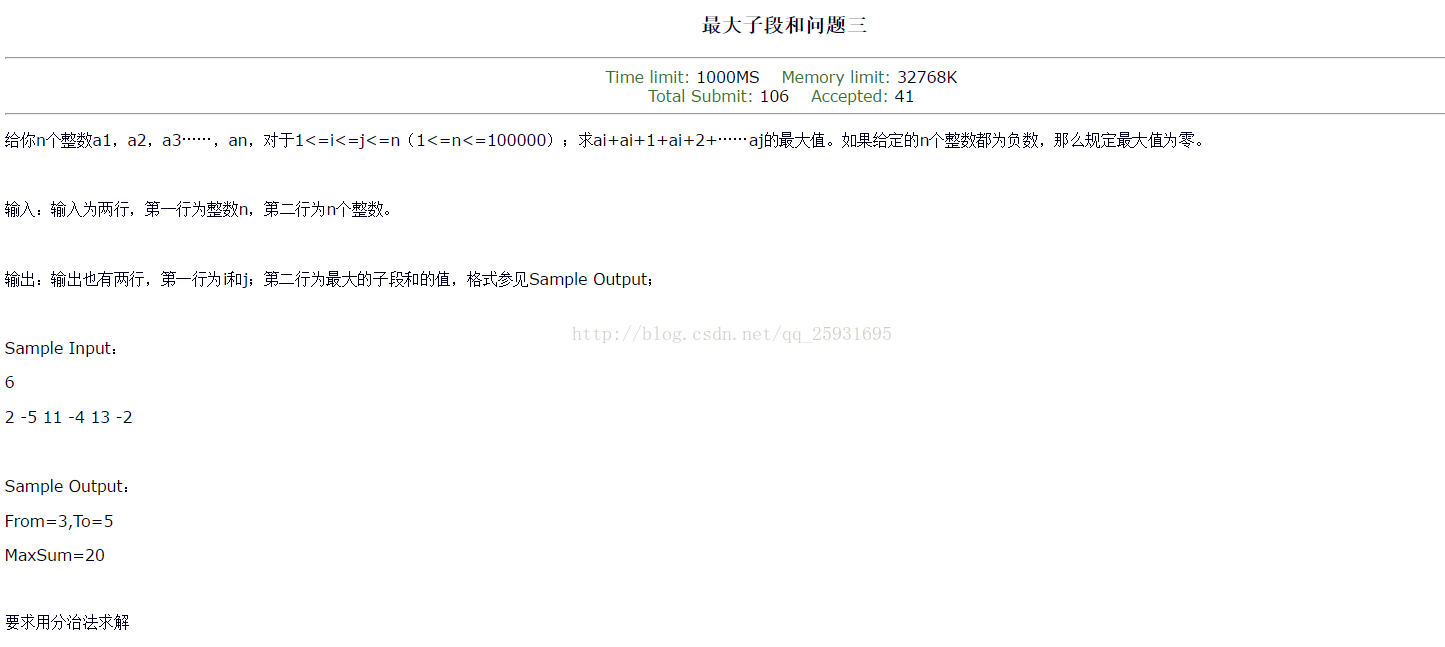
结果显示：

弊端：容易T，起始点和终止点的求取不准确，在1 -1 3中应该是3 3 3 ，无法做妥善处理。

方案二：二层枚举，可行性❤❤

将方案一进行优化，发现k层循环并没有任何必要，2层枚举就够了，时间复杂度为O（n^2）

直接从起点开始即可。

可行性范围：n<=1000

#include <iostream>
using namespace std;
#define N 101
int node[N];
int main()
{
    int n;
    while(cin>>n)
    {
        int i;
        for(i=1;i<=n;i++)
            cin>>node[i];
        //二层枚举求最大和
        int maxsum=0,tmpsum=0;
        int from=0,to=0;
        int j,k;
        for (i=1;i<=n;i++)
       {
       		 tmpsum = 0;
        	for (j=i;j<=n;j++)
            {
            	tmpsum += node[j];
            	if (tmpsum>maxsum)
				{
                  maxsum = tmpsum;
                  from=i;
                  to=j;
				}
            }
        }
        cout<<"From="<<from<<",To="<<to<<endl;
        cout<<"MaxSum="<<maxsum<<endl;
    }
    return 0;
}

结果显示：

弊端：方案一相同，起始点和终止点的求取不准确，在1 -1 3中应该是3 3 3 ，无法做妥善处理

方案三：分治，可行性❤❤❤

从上述两种方案中会发现当n很大时，就会超时，那么有没有更快的算法呢？然后就有了分治，时间复杂度为O（nlogn）

分治思想：分而治之，不懂的可以去看http://blog.csdn.net/qq_25931695/article/details/51125800

求子区间及最大和，从结构上是非常适合分治法的，因为所有子区间[start, end]只可能有以下三种可能性:

      在[1, n/2]这个区域内

      在[n/2+1, n]这个区域内

      起点位于[1,n/2],终点位于[n/2+1,n]内

需要注意的是，在求取起始点和终止点的时候在递归里带参传递的时候的处理。

可行性范围：n<=100000

#include <stdio.h>
#define N 100005
int a[N];
struct node
{
	int tfrom;
	int tto;
	int tsum;
};
node getMaxsum(int left,int right);
void print(node ans);
int main()
{
    int n;
    while(~scanf("%d",&n))
    {
        int i;
        for(i=1;i<=n;i++)
        {
            scanf("%d",&a[i]);
        }
        node an=getMaxsum(1,n);
        print(an);
    }
    return 0;
}
node getMaxsum(int left,int right)
{
    int i;
    node ret;
    if(left==right)
    {
        if(a[left]>0)
        {
             ret.tsum=a[left];
             ret.tfrom=left;
             ret.tto=right;
        }
        else 
	{
             ret.tsum=0;
             ret.tfrom=1;
             ret.tto=1;
	}
    }
    else
    {
        int center=(left+right)/2;
        node maxleft,maxright;
        maxleft=getMaxsum(left,center);
        maxright=getMaxsum(center+1,right);
        int ans1=0,ans2=0;
        int s1=0,s2=0;
        int pi=center+1,pj=center;//这里需要特别注意
        for(i=center;i>=left;i--)
        {
            ans1+=a[i];
            if(ans1>s1)
            {
                s1=ans1;
                pi=i;
            }
        }
        for(i=center+1;i<=right;i++)
        {
            ans2+=a[i];
            if(ans2>s2)
            {
                s2=ans2;
                pj=i;
            }
        }
        ret.tsum=s1+s2;
        ret.tfrom=pi;
        ret.tto=pj;
        if((ret.tsum<=maxleft.tsum) && (maxright.tsum<=maxleft.tsum))
        {
            ret.tsum=maxleft.tsum;
            ret.tfrom=maxleft.tfrom;
            ret.tto=maxleft.tto;
        }
        else if(ret.tsum<maxright.tsum)
        {
            ret.tsum=maxright.tsum;
            ret.tfrom=maxright.tfrom;
            ret.tto=maxright.tto;
        }
    }
    return ret;
}
void print(node ans)
{
	printf("From=%d,To=%d\nMaxSum=%d\n",ans.tfrom,ans.tto,ans.tsum);
}

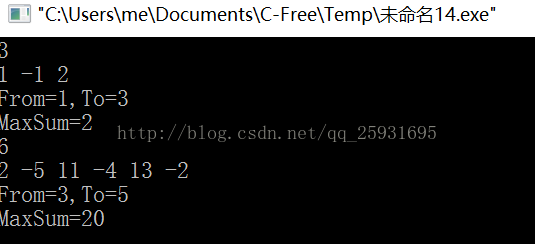
结果显示：

弊端：发现方案一跟方案二存在的问题解决了，但是可以更进一步优化，万一N很大怎么办呢？

方案四：动态规划，可行性❤❤❤❤

动态规划的过程是：每次决策依赖于当前状态，又随即引起状态的转移。一个决策序列就是在变化的状态中产生的。

所以，关键就是找出状态方程。

这题，假设F(i)表示以位置i为终点的所有子区间中和最大的一个

子问题：如i为终点的最大子区间包含了位置i-1，则以i-1为终点的最大子区间必然包括在其中

如果F[i-1]>0，那么显然F[i]=f[i-1]+a[i]

如果F[i-1]<=0，那么F[i]=a[i],因为既然最大，前面的负数必然不能使之最大

这样，状态转移方程就有了，那么接下来的问题就不是问题了。

你会发现，这样i只要遍历一次就行，其时间复杂度为O（n）

可行性范围：n<=1000000

#include <iostream>
#include <string.h>
using namespace std;
#define N 1000001
int a[N];
int F[N];
int n;
void Init();
void Input();
void OutMax();
int main()
{
    while(cin>>n)
    {
        Init();
        Input();
        OutMax();
    }
    return 0;
}
void Init()
{
    memset(F,0,sizeof(F));
}
void Input()
{
    int i;
    for(i=1; i<=n; i++)
    {
        cin>>a[i];
    }
}
void OutMax()
{
    int i;
    int pi=1,pj=1;
    int ans=a[1],ti=1;
    F[1]=a[1];
    for(i=2; i<=n; i++)
    {
        if(F[i-1]>0)
        {

            F[i]=F[i-1]+a[i];
        }
        else
        {
            F[i]=a[i];
            ti=i;
        }
        if(F[i]>ans)
        {
            ans=F[i];
            pi=ti;
            pj=i;
        }
    }
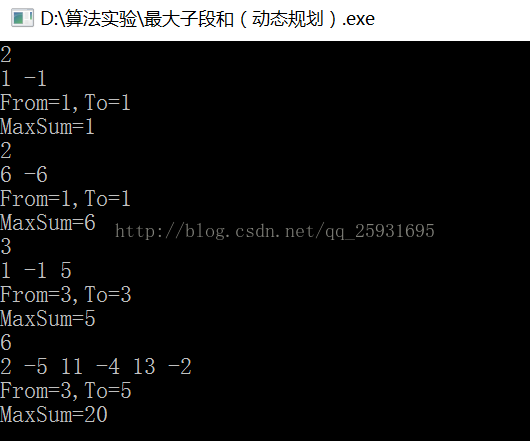
    cout<<"From="<<pi<<",To="<<pj<<endl<<"MaxSum="<<ans<<endl;
}

结果显示：

四个方案各有优缺点，当然动态规划的是最准确最快速的啦，不过让人难以想到啊~

最大子段和问题就讲到这里了，还有不懂的留言吧~我想我应该讲的已经很清楚了~