题意:给你一个整数n,求n的划分种类总数
这是一道很经典的整数划分问题。
所谓整数划分,是指把一个正整数n写成如下形式:
n=m1+m2+...+mi; (其中mi为正整数,并且1 <= mi <= n),则{m1,m2,...,mi}为n的一个划分。
如果{m1,m2,...,mi}中的最大值不超过m,即max(m1,m2,...,mi)<=m,则称它属于n的一个m划分。
思路:
一、递归法
我们将最大加数不大于m的划分个数记作q(n,m).
可以建立q(n,m)的如下递归关系:
(1)q(n,1)=1,n>=1
当最大加数不大于1时,任何正整数n只有一种划分形式,即1+1+1+……+1
(2)q(n,m)=q(n,n),m>=n
最大加数实际上不能大于n,因此q(1,m)=1
(3)q(n,n)=1+q(n,n-1)
正整数n的划分有最大加数=n的划分和最大加数<=n-1的划分组成
(4)q(n,m)=q(n,m-1)+q(n-m,m), n>m>1
正整数n的最大加数不大于m的划分由最大加数=m的划分和划分和最大加数<=m-1的划分组成
这里大家有可能不是很理解,为什么是这样呢?所以我详细讲解下:
(a). 划分中包含 m 的情况,即 { m, { x1, x2, ..., xi } }, 其中 { x1, x2, ..., xi } 的和为 n - m,可能再次出现 m,因此是(n - m)的 m 划分,因此这种划分个数为 q(n-m, m);
(b). 划分中不包含 m 的情况,则划分中所有值都比 m 小,即 n 的 ( m - 1 ) 划分,个数为 q(n, m - 1);
即
#include <cstdio>
int n,ans;
int fix(int pn,int pm);
int main()
{
while(~scanf("%d",&n))
{
ans=0;
ans=fix(n,n);
printf("%d\n",ans);
}
return 0;
}
int fix(int pn,int pm)
{
if(pn==1 || pm==1)return 1;
if(pn<pm)return fix(pn,pn);
if(pn==pm)return 1+fix(pn,pm-1);
return fix(pn,pm-1)+fix(pn-pm,pm);
}
二、动态规划
dp[i][j]表示整数i的划分中,每个数不大于j的划分数
(1)dp[ i ][ j ]=dp[ i ][ j-1 ]+dp[ i-j ][ j ] i>=j
(2)dp[ i ][ j ]=do[ i ][ i ] i<j
#include<iostream>
#include<cstring>
using namespace std;
const int maxn=10010;
int dp[maxn][maxn],n,m;
void sovle()
{
dp[0][0]=1;
int i,j;
for(i=1; i<=n; i++)
{
dp[i][1] = dp[1][i] = dp[0][i] = 1;
}
for(i=2; i<=n; i++)
{
for(j=2; j<=n; j++)
{
if(j<=i)
dp[i][j] = dp[i][j-1] + dp[i-j][j];
else
dp[i][j] = dp[i][i];
}
}
}
int main()
{
memset(dp,0,sizeof(dp));
while(~scanf("%d",&n))
{
sovle();
cout<<dp[n][n]<<endl;
}
return 0;
} 三、母函数 (参考了http://www.cnblogs.com/hoodlum1980/archive/2008/10/11/1308493.html)
下面我们从另一个角度即“母函数”的角度来考虑这个问题。
所谓母函数,即为关于x的一个多项式G(x):
有 G(x)= a0 + a1*x + a2*x^2 + a3*x^3 + ...
则我们称G(x)为序列(a0,a1,a2,...)的母函数。关于母函数的思路我们不做更多分析。
我们从整数划分考虑,假设n的某个划分中,1的出现个数记为a1,2的个数记为a2,..., i的个数记为ai,
显然: ak<=n/k; (0<= k <=n)
因此n的划分数f(n,n),也就是从1到n这n个数字中抽取这样的组合,每个数字理论上可以无限重复出现,即个数随意,使他们的总和为n。显然,数字i可以有如下可能,出现0次(即不出现),1次,2次,..., k次,等等。把数字i用(x^i)表示,出现k次的数字i用 x^(i*k)表示, 不出现用1表示。例如数字2用x^2表示,2个2用x^4表示,3个2用x^6表示,k个2用x^2k表示。
则对于从1到N的所有可能组合结果我们可以表示为:
G(x) = (1+x+x^2+x^3+...+x^n) (1+x^2+x^4+...) (1+x^3+x^6+...) ... (1+x^n)
= g(x,1) g(x,2) g(x,3) ... g(x, n)
= a0 + a1* x + a2* x^2 + ... + an* x^n + ... ; (展开式)
上面的表达式中,每一个括号内的多项式代表了数字i的参与到划分中的所有可能情况。因此该多项式展开后,由于x^a * x^b=x^(a+b),因此 x^i 就代表了i的划分,展开后(x^i)项的系数也就是i的所有划分的个数,即f(n,n)=an (上式中g(x,i)表示数字i的所有可能出现情况)。
由此我们找到了关于整数划分的母函数G(x);剩下的问题是,我们需要求出G(x)的展开后的所有系数。
为此我们首先要做多项式乘法,对于我们来说并不困难。我们把一个关于x的一元多项式用一个整数数组a[]表示,a[i]代表x^i的系数,即:
g(x) = a[0] + a[1]x + a[2]x^2 + ... + a[n]x^n;
则关于多项式乘法的代码如下,其中数组a和数组b表示两个要相乘的多项式,结果存储到数组c:
#define N 130
unsigned long a[N];/*多项式a的系数数组*/
unsigned long b[N];/*多项式b的系数数组*/
unsigned long c[N];/*存储多项式a*b的结果*/
/*两个多项式进行乘法,系数分别在a和b中,结果保存到c ,项最大次数到N */
/*注意这里我们只需要计算到前N项就够了。*/
void Poly()
{
int i,j;
memset(c,0,sizeof(c));
for(i=0; i<N; i++)
for(j=0; j<N-i; j++) /*y<N-i: 确保i+j不会越界*/
c[i+j] += a[i]*b[j];
}下面我们求出G(x)的展开结果,G(x)是n个多项式连乘的结果:
/*计算出前N项系数!即g(x,1) g(x,2)... g(x,n)的展开结果*/
void Init()
{
int i,k;
memset(a,0,sizeof(a));
memset(c,0,sizeof(c));
for(i=0;i<N;i++) a[i]=1; /*第一个多项式:g(x, 1) = x^0 + x^1 + x^2 + x^3 + */
for(k=2;k<N;k++)
{
memset(b,0,sizeof(b));
for(i=0;i<N;i+=k) b[i]=1;/*第k个多项式:g(x, k) = x^0 + x^(k) + x^(2k) + x^(3k) + */
Poly(); /* 多项式乘法:c= a*b */
memcpy(a,c,sizeof(c)); /*把相乘的结果从c复制到a中:c=a; */
}
}通过以上的代码,我们就计算出了G(x)的展开后的结果,保存到数组c中。此时有:f(n,n)=c[n];剩下的工作只是把相应的数组元素输出即可。
问题到了这里已经解决完毕。但我们发现,针对该问题,g(x,k)是一个比较特殊的多项式,特点是只有k的整数倍的索引位置有项,而其他位置都为0,具有项“稀疏”的特点,并且项次分布均匀(次数跨度为k)。这样我们就可以考虑在计算多项式乘法时,可以减少一些循环。因此可以对Poly函数做这样的一个改进,即把k作为参数传递给Poly:
/*两个多项式进行乘法,系数分别在a和b中,结果保存到c ,项最大次数到N */
/*改进后,多项式a乘以一个有特殊规律的多项式b,即b中只含有x^(k*i)项,i=0,1,2,*/
/*如果b没有规律,只需要把k设为1,即与原来函数等效*/
void Poly2(int k) /*参数k的含义:表示b中只有b[k*i]不为0!*/
{
int i,j;
memset(c,0,sizeof(c));
for(i=0; i<N; i++)
for(j=0; j<N-i; j+=k)
c[i+j] += a[i]*b[j];
}
整体代码如下:
#include <iostream>
#include <string.h>
using namespace std;
#define N 130
typedef long long LL;
LL a[N],b[N],c[N];
int n;
void Poly(int m);
void Init();
int main()
{
Init();
while(cin>>n)
{
cout<<c[n]<<endl;
}
return 0;
}
void Poly(int m)
{
int i,j;
memset(c,0,sizeof(c));
for(i=0;i<N;i++)
{
for(j=0;j<N-i;j+=m) //简化这样求得最大系数就是c[N]
{
c[i+j]+=a[i]*b[j]; //(ma^x)*(na^y)=mn*a^(x+y)
}
}
}
void Init()
{
memset(a,0,sizeof(a));
memset(c,0,sizeof(c));
int i;
for(i=0;i<N;i++)
{
a[i]=1;
}
int k;
for(k=2;k<N;k++)
{
memset(b,0,sizeof(b));
for(i=0;i<N;i+=k)
{
b[i]=1;
}
Poly(k);
memcpy(a,c,sizeof(c));
}
}
母函数这个方法我是想不到的,请原谅我才疏学浅,不过学会如何获取知识也是种能力,所以大家碰到不会的也不要气馁,看看前人是否已经给你做好充足的准备!











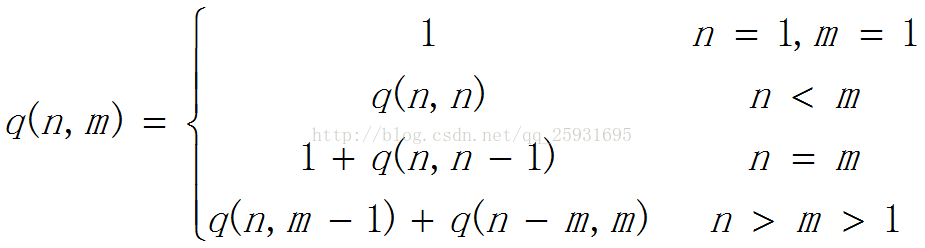
















 1321
1321

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








