PID控制器通过比例、积分、微分三环节调节系统，位置式适用于精确位置控制，增量式适合快速响应速度变化。比例环节影响动态响应，积分环节消除稳态误差，微分环节改善动态特性。文章提供了代码示例和调节PID参数的方法。
目录
一、介绍
PID控制器是一种广泛应用的调节器控制规律，其核心在于通过比例（P）、积分（I）和微分（D）三个环节对控制目标进行精确调节。这种控制方法主要适用于基本线性和动态特性不随时间变化的系统。
在PID控制中，比例环节的作用是根据偏差e的大小调整控制器的输出信号u，使系统能够快速响应偏差的变化。然而，过大的比例系数Kp可能导致系统产生激烈的振荡和不稳定，因此在设计时需要合理优化Kp。
积分环节的作用是对偏差e进行积分，以实现无差调节。当系统平衡后，偏差为0，积分控制器的输出不再发生变化。积分环节有助于消除系统的稳态误差，但积分作用过强可能导致系统响应过慢。
微分环节则是根据偏差e的变化率调整控制器的输出信号u，有助于改善系统的动态特性，减小超调和振荡。然而，微分环节对噪声干扰信号敏感，需要在实际应用中加以注意。
位置式PID和增量式PID是PID控制的两种主要形式。
位置式PID是一种位置闭环控制方法。它根据编码器的脉冲累加测量电机的位置信息，并与目标值进行比较得到控制偏差。然后，通过对偏差进行比例、积分、微分的控制，使偏差趋近于0。这种方法通常应用于需要精确位置控制的场合，如舵机控制等。
增量式PID则是一种速度闭环控制方法。它根据单位时间获取的脉冲数测量电机的速度信息，并与目标值进行比较得到控制偏差。同样地，通过对偏差进行比例、积分、微分的控制，使偏差趋近于0。增量式PID关注的是控制量的增量，适用于需要快速响应速度变化的场合。
总的来说，PID控制器通过比例、积分和微分三个环节的组合，实现了对控制目标的精确调节。位置式PID和增量式PID则分别适用于不同的控制需求，为各种工业控制系统提供了有效的解决方案。
PID三个环节各自的主要作用和效应：
- 比例环节：起主要控制作用，使控制量向目标值靠拢，但可能导致振荡
- 积分环节：消除稳态误差，但会增加超调量
- 微分环节：产生阻尼效果，抑制振荡和超调，但会降低响应速度
二、位置式PID控制
1. 位置型PID特点
1、位置型PID控制的输出与整个过去的状态有关，用到了偏差的累加值，容易产生累积偏差。
2、位置型PID适用于执行机构不带积分部件的对象。的强弱取决于积分时间常数T,T越大，积分作用越弱，反之则越强。
3、位置型的输出直接对应对象的输出，对系统的影响比较大。
2. 比例系数与积分时间的大小对曲线的影响关系
(1) 比例环节
成比例地反映控制系统的偏差信号e(t)，偏差一旦产生，控制器立即产生控制作用，以减小偏差。当仅有比例控制时系统输出存在稳态误差（Steady-state error）。
P参数越大比例作用越强，动态响应越快，消除误差的能力越强。但实际系统是有惯性的，控制输出变化后，实际y(t)值变化还需等待一段时间才会缓慢变化。由于实际系统是有惯性的，比例作用不宜太强，比例作用太强会引起系统振荡不稳定。P参数的大小应在以上定量计算的基础上根据系统响应情况，现场调试决定，通常将P参数由大向小调，以能达到最快响应又无超调(或无大的超调)为最佳参数。
优点:调整系统的开环比例系数，提高系统的稳态精度，减低系统的惰性，加快响应速度。
缺点:仅用P控制器,过大的开环比例系数不仅会使系统的超调量增大，而且会使系统稳定裕度变小，甚至不稳定。
(2) 积分环节
控制器的输出与输入误差信号的积分成正比关系。主要用于消除静差，提高系统的无差度。积分作用的强弱取决于积分时间常数T,T越大，积分作用越弱，反之则越强。
对一个自动控制系统，如果在进入稳态后存在稳态误差，则称这个控制系统是有稳态误差的或简称有差系统（System with Steady-state Error）。为了消除稳态误差，在控制器中必须引入“积分项”。积分项对误差取决于时间的积分，随着时间的增加，积分项会增大。这样，即便误差很小，积分项也会随着时间的增加而加大，它推动控制器的输出增大使稳态误差进一步减小，直到等于零。因此，比例+积分(PI)控制器，可以使系统在进入稳态后无稳态误差。PI控制器不但保持了积分控制器消除稳态误差的“记忆功能”，而且克服了单独使用积分控制消除误差时反应不灵敏的缺点。
优点：消除稳态误差。
缺点：积分控制器的加入会影响系统的稳定性，使系统的稳定裕度减小。
(3) 微分环节
反映偏差信号的变化趋势，并能在偏差信号变得太大之前，在系统中引入一个有效的早期修正信号，从而加快系统的动作速度，减少调节时间。在微分控制中，控制器的输出与输入误差信号的微分（即误差的变化率）成正比关系。
自动控制系统在克服误差的调节过程中可能会出现振荡甚至失稳。其原因是由于存在有较大惯性组件（环节）或有滞后(delay)组件，具有抑制误差的作用，其变化总是落后于误差的变化。解决的办法是使抑制误差的作用的变化“超前”，即在误差接近零时，抑制误差的作用就应该是零。这就是说，在控制器中仅引入“比例”项往往是不够的，比例项的作用仅是放大误差的幅值，而目前需要增加的是“微分项”，它能预测误差变化的趋势。这样，具有比例+微分的控制器，就能够提前使抑制误差的控制作用等于零，甚至为负值，从而避免了被控量的严重超调。所以对有较大惯性或滞后的被控对象，比例+微分(PD)控制器能改善系统在调节过程中的动态特性。PD控制只在动态过程中才起作用，对恒定稳态情况起阻断作用。因此，微分控制在任何情况下都不能单独使用。
优点：使系统的响应速度变快，超调减小，振荡减轻，对动态过程有“预测”作用。
在低频段，主要是PI控制规律起作用，提高系统型别，消除或减少稳态误差；在中高频段主要是PD规律起作用，增大截止频率和相角裕度，提高响应速度。因此，控制器可以全面地提高系统的控制性能。
3. PID各值对控制系统影响关系
（1） 比例（P）参数
- 增大P值：
- 提高响应速度：系统的响应速度会加快，动作更加灵敏。
- 减小静差：在系统稳定的情况下，增大比例系数可以减小系统的稳态误差，提高控制精度。
- 稳定性影响：但过大的比例系数会导致系统产生振荡，调节时间拉长，甚至可能使系统不稳定。
- 减小P值：
- 降低响应速度：系统的响应速度会变慢。
- 增大静差：系统的稳态误差会增大，控制精度降低。
（2） 积分（I）参数
- 增大I值：
- 减小静差：积分控制引入了过去误差的累积，能够进一步减小甚至消除系统的稳态误差，提高控制精度。
- 稳定性影响：但过大的积分值会导致系统振荡次数增加，甚至使系统不稳定。
- 减小I值：
- 增大静差：积分作用减弱，系统稳态误差增大。
- 提高稳定性：在一定程度上可以提高系统的稳定性，但可能会牺牲控制精度。
（3）微分（D）参数
- 增大D值：
- 改善动态性能：微分控制通过预测误差的变化趋势，提前进行修正，可以减少系统的超调量，缩短调节时间。
- 稳定性影响：但过大的微分值会放大噪声，对系统稳定性产生负面影响。
- 减小D值：
- 降低动态性能：系统的响应速度可能变慢，超调量增大，调节时间延长。
- 提高稳定性：在一定程度上可以提高系统的稳定性，但可能会牺牲动态性能。
4. 代码示例
完整代码链接：https://download.csdn.net/download/qq_26043945/89145970
//进行一次pid计算（每次调用间隔一段时间）
//参数为(pid结构体,setpoint目标值,feedback反馈值)，计算结果放在pid结构体的output成员中
void PID_Calc(PID *pid,float setpoint,float feedback){
// 误差
pid.error = setpoint - feedback;
// 累积误差
pid.integral = pid.integral + pid.error;
// 累积误差限幅
if(pid.integral > pid.maxIntegral) pid.integral = pid.maxIntegral;
else if(pid.integral < -pid.maxIntegral) pid.integral = -pid.maxIntegral;
// 计算输出值
pid.output = pid.error * pid.kp + pid.integral * pid.ki + (pid.error - pid.lastError) * pid.kd;
// 更新上一误差
pid.lastError = pid.error;
}
5. 实际曲线调节PID各环节的方式
(1) 控制 Kp 变量
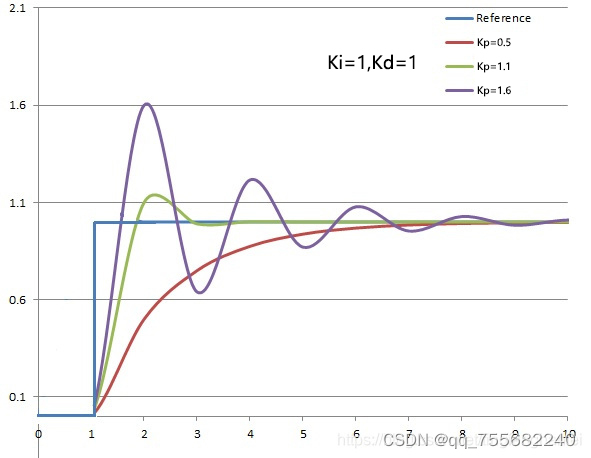
(2) 控制 Ki 变量
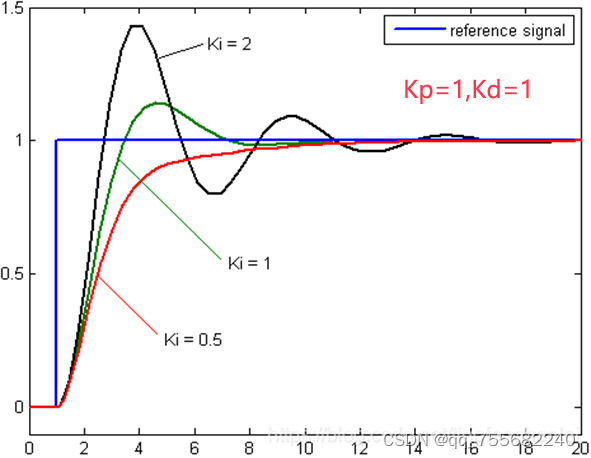
(3) 控制 Kd 变量
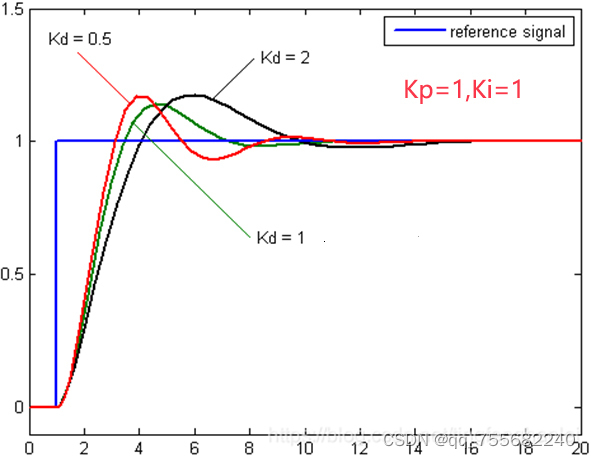
(4) 实际演示效果
二、增量式PID控制
1. 增量型PID特点
1、增量型PID算法不需要做累加，控制量增量的确定仅与最近几次偏差值有关，计算偏差的影响较小。
2、增量型PID算法得出的是控制量的增量，对系统的影响相对较小。
3、采用增量型PID算法易于实现手动到自动的无扰动切换。
从下面可以看出，由于位置式PID里面存在积分信号，容易产生累积偏差，在达到设定值时会存在震荡，这里的小人运动到墙面处就需要停止，就不能有震荡。增量式PID只带入了前两次的误差，所以不容易震荡，所以更适合用在下面的这种情况。
2. 代码示例
#include <stdio.h>
// 增量式PD控制器结构体
typedef struct {
float Kp; // 比例系数
float Kd; // 微分系数
float error; // 当前误差（此字段将在控制函数内部更新）
float prev_error; // 上一次误差
float prev_prev_error; // 上上次误差
float setpoint; // 设定值
} PDController;
// 初始化PD控制器函数
void initPDController(PDController* pd, float Kp, float Kd, float setpoint) {
pd->Kp = Kp;
pd->Kd = Kd;
pd->error = 0;
pd->prev_error = 0;
pd->prev_prev_error = 0;
pd->setpoint = setpoint;
}
// 增量式PD控制函数
void incrementalPDControl(PDController* pd, float feedback, float* output_PWM) {
// 计算当前误差
pd->error = pd->setpoint - feedback;
// 计算增量式PD（不包含积分项）
float add = pd->Kp * (pd->error - pd->prev_error) + pd->Kd * (pd->error - 2 * pd->prev_error + pd->prev_prev_error);
// 计算最终的PD输出
*output_PWM += add;
// 更新状态
pd->prev_prev_error = pd->prev_error;
pd->prev_error = pd->error;
}
int main() {
// 声明PD控制器结构体变量
PDController pd;
float output_PWM = 0; // PWM输出变量
float feedback = 0; // 实际测量值（这里应该是一个动态变化的值，但为了示例我们固定为0）
// 初始化PD控制器
initPDController(&pd, 1.0, 0.1, 10.0);
// 调用增量式PD控制函数
incrementalPDControl(&pd, feedback, &output_PWM);
// 打印PWM输出（仅用于示例）
printf("PWM Output: %f\n", output_PWM);
return 0;
}
扫一扫
2782
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
