pageRank算法
算法思想
用结点表示网站,用有向边表示结点网站之间的超链接关系,如果网站1有通向网站2的超链接则在结点1和2之间连一条有向边,方向 1 → 2 1\rightarrow 2 1→2
如此建立有向图网络表示网站的链接情况.
现在给定一些网站,要求根据有向图网络给这些网站的重要性做出排序
由社会网络分析法可知,有向图中的一个结点的重要性可以通过其中心性,特征向量中心性等来衡量
如果通过点度中心性衡量,则只需要根据每个结点的入度从大到小排序,
但这忽略了一个"近朱者赤近墨者黑"的事实----重要的网站链接到的网站一般也是重要的.
那么就需要考虑邻居结点重要性.
于是更优的衡量方法是特征向量中心性来衡量.
数量假设:一个网站的入链越多,这个网站越重要
质量假设:被重要网站引用的网站也是重要的
输入n,m表示有n个结点,m条有向边的网络.以此输入m对 u , v u,v u,v表示存在一条从u到v的有向边.建立有向图网络
设 u i u_i ui为第i个网站,记 P R ( u i ) PR(u_i) PR(ui)为点 u i u_i ui的 p a g e r a n k pagerank pagerank值, O ( u i ) O(u_i) O(ui)表示结点 u i u_i ui的出度,
初始时我们给定这n个结点有相同的排名,即任意结点的PR值都是 1 n \frac{1}{n} n1
此后我们用迭代的方法求每个点的PR值,记
P
R
k
(
u
i
)
PR_k(u_i)
PRk(ui)为第k次迭代后结点
u
i
u_i
ui的PR值
P
R
k
+
1
(
u
i
)
=
∑
j
=
1
,
j
≠
i
n
P
R
k
(
u
j
)
O
(
u
j
)
=
∑
j
=
1
n
g
j
i
P
R
k
(
u
j
)
O
(
u
j
)
PR_{k+1}(u_i)=\sum_{j=1,j≠i}^n\frac{PR_k(u_j)}{O(u_j)}=\sum_{j=1}^n\frac{g_{ji}PR_k(u_j)}{O(u_j)}
PRk+1(ui)=j=1,j=i∑nO(uj)PRk(uj)=j=1∑nO(uj)gjiPRk(uj)
其中
g
i
j
g_{ij}
gij为联通矩阵
G
n
×
n
G_{n\times n}
Gn×n的元素
g
i
j
=
{
0
,
<
u
i
,
u
j
>
不
存
在
1
,
<
u
i
,
u
j
>
存
在
g_{ij}=\begin{cases} 0,<u_i,u_j>不存在\\ 1,<u_i,u_j>存在 \end{cases}
gij={0,<ui,uj>不存在1,<ui,uj>存在
那么公式又可以写为
P
R
k
+
1
(
u
i
)
=
[
g
1
i
O
(
u
1
)
g
2
i
O
(
u
2
)
.
.
.
g
n
i
O
(
u
n
)
]
[
P
R
k
(
u
1
)
P
R
k
(
u
2
)
.
.
.
P
R
k
(
u
n
)
]
=
[
g
1
i
g
2
i
.
.
.
g
n
i
]
[
1
O
(
u
1
)
1
O
(
u
2
)
.
.
.
1
O
(
u
n
)
]
[
P
R
k
(
u
1
)
P
R
k
(
u
2
)
.
.
.
P
R
k
(
u
n
)
]
\begin{aligned} PR_{k+1}(u_i)=& [\frac{g_{1i}}{O(u_1)}\ \frac{g_{2i}}{O(u_2)}\ ...\ \frac{g_{ni}}{O(u_n)}] \begin{bmatrix} PR_k(u_1)\\ PR_k(u_2)\\ ...\\ PR_k(u_n) \end{bmatrix}\\ &=[g_{1i}\ g_{2i}\ ...\ g_{ni}] \begin{bmatrix} \frac{1}{O(u_1)}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \frac{1}{O(u_2)}\ \ \ \ \ \\ ...\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{1}{O(u_n)} \end{bmatrix} \begin{bmatrix} PR_k(u_1)\\ PR_k(u_2)\\ ...\\ PR_k(u_n) \end{bmatrix} \end{aligned}
PRk+1(ui)=[O(u1)g1i O(u2)g2i ... O(un)gni]⎣⎢⎢⎡PRk(u1)PRk(u2)...PRk(un)⎦⎥⎥⎤=[g1i g2i ... gni]⎣⎢⎢⎡O(u1)1 O(u2)1 ... O(un)1⎦⎥⎥⎤⎣⎢⎢⎡PRk(u1)PRk(u2)...PRk(un)⎦⎥⎥⎤
令 V k = [ P R k ( u 1 ) P R k ( u 2 ) . . . P R k ( u n ) ] \mathbf V_k=\begin{bmatrix}PR_k(u_1)\\PR_k(u_2)\\...\\PR_k(u_n)\end{bmatrix} Vk=⎣⎢⎢⎡PRk(u1)PRk(u2)...PRk(un)⎦⎥⎥⎤表示第k次迭代之后的PR特征向量
那么有
V
k
=
[
g
11
g
21
g
31
.
.
.
g
n
1
g
12
g
22
g
32
.
.
.
g
n
2
g
13
g
23
g
33
.
.
.
g
n
3
.
.
.
g
1
n
g
2
n
g
3
n
.
.
.
g
n
n
]
[
1
O
(
u
1
)
1
O
(
u
2
)
1
O
(
u
3
)
.
.
.
1
O
(
u
n
)
]
V
k
−
1
\mathbf {V_k}= \begin{bmatrix} g_{11}\ g_{21}\ g_{31}\ ...\ g_{n1}\\ g_{12}\ g_{22}\ g_{32}\ ...\ g_{n2}\\ g_{13}\ g_{23}\ g_{33}\ ...\ g_{n3}\\ ...\\ g_{1n}\ g_{2n}\ g_{3n}\ ...\ g_{nn} \end{bmatrix} \begin{bmatrix} \frac{1}{O(u_1)}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \frac{1}{O(u_2)}\ \ \ \ \ \ \ \ \ \ \ \ \\ \ \ \ \ \ \ \ \ \frac{1}{O(u_3)}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ...\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{1}{O(u_n)} \end{bmatrix} \mathbf{V_{k-1}}
Vk=⎣⎢⎢⎢⎢⎡g11 g21 g31 ... gn1g12 g22 g32 ... gn2g13 g23 g33 ... gn3...g1n g2n g3n ... gnn⎦⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎢⎡O(u1)1 O(u2)1 O(u3)1 ... O(un)1⎦⎥⎥⎥⎥⎥⎤Vk−1
令
Λ
=
[
1
O
(
u
1
)
1
O
(
u
2
)
1
O
(
u
3
)
.
.
.
1
O
(
u
n
)
]
\Lambda=\begin{bmatrix} \frac{1}{O(u_1)}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \frac{1}{O(u_2)}\ \ \ \ \ \ \ \ \ \ \ \ \\ \ \ \ \ \ \ \ \ \frac{1}{O(u_3)}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ...\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{1}{O(u_n)} \end{bmatrix}
Λ=⎣⎢⎢⎢⎢⎢⎡O(u1)1 O(u2)1 O(u3)1 ... O(un)1⎦⎥⎥⎥⎥⎥⎤
则有 V k = G T Λ V k − 1 \mathbf{V_k}=\mathbf{G^T\Lambda V_{k-1}} Vk=GTΛVk−1
令 M = G T Λ \mathbf M=\mathbf{G^T\Lambda} M=GTΛ为概率转移矩阵则有 V k = M V k − 1 \mathbf{V_k}=\mathbf{M V_{k-1}} Vk=MVk−1即迭代公式
M还可以通过观察写出,M的第i列为结点i的转移概率向量,假设i有三个出度,分别指向x,y,z三个结点
则M的第i列只有第x,y,z三行同为 1 3 \frac{1}{3} 31,其余各行为0
那么 V k = M k V 0 \mathbf V_k=\mathbf M^{k} \mathbf V_0 Vk=MkV0
其中 V 0 = [ 1 n 1 n 1 n . . . 1 n ] \mathbf V_0=\begin{bmatrix}\frac{1}{n}\\\frac{1}{n}\\\frac{1}{n}\\...\\\frac{1}{n}\\\end{bmatrix} V0=⎣⎢⎢⎢⎢⎡n1n1n1...n1⎦⎥⎥⎥⎥⎤
例如
如图所示,该有向图网络的联通矩阵为
G = [ 0 1 0 0 1 0 1 0 0 0 0 1 1 0 1 0 ] \mathbf G=\begin{bmatrix} 0\ 1\ 0\ 0\\ 1\ 0\ 1\ 0\\ 0\ 0\ 0\ 1\\ 1\ 0\ 1\ 0 \end{bmatrix} G=⎣⎢⎢⎡0 1 0 01 0 1 00 0 0 11 0 1 0⎦⎥⎥⎤
各个结点的出度为 1 , 2 , 1 , 2 1,2,1,2 1,2,1,2
Λ = [ 1 0 0 0 0 1 2 0 0 0 0 1 0 0 0 0 1 2 ] \mathbf \Lambda=\begin{bmatrix} 1\ 0\ 0\ 0\\ 0\ \frac{1}{2}\ 0\ 0\\ 0\ 0\ 1\ 0\\ 0\ 0\ 0\ \frac{1}{2}\\ \end{bmatrix} Λ=⎣⎢⎢⎡1 0 0 00 21 0 00 0 1 00 0 0 21⎦⎥⎥⎤M = G T Λ = [ 0 1 2 0 1 2 1 0 0 0 0 1 2 0 1 2 0 0 1 0 ] \mathbf M=\mathbf{G^T\Lambda}= \begin{bmatrix} 0\ \frac{1}{2}\ 0\ \frac{1}{2}\\ 1\ 0\ 0\ 0\\ 0\ \frac{1}{2}\ 0\ \frac{1}{2}\\ 0\ 0\ 1\ 0 \end{bmatrix} M=GTΛ=⎣⎢⎢⎡0 21 0 211 0 0 00 21 0 210 0 1 0⎦⎥⎥⎤
迭代之后发现 V \mathbf V V为定值,但是貌似1和3的入度为2应该更加重要,实际上是质量假设起了作用
dead ends问题及修正
前述情况只考虑了每个站点都会有指向其他站点的链接,也就是每个结点都有出度;
但是网络上也有只进不出的网站,现在考虑如果某个结点没有出度:
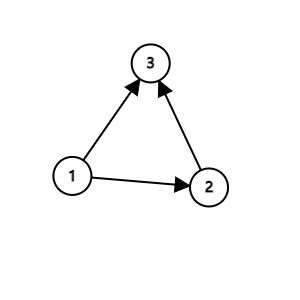
观察可得
M
=
[
0
0
0
1
2
0
0
1
2
1
0
]
\mathbf M=\begin{bmatrix} 0\ 0\ 0\\ \frac{1}{2}\ 0\ 0\\ \frac{1}{2}\ 1\ 0 \end{bmatrix}
M=⎣⎡0 0 021 0 021 1 0⎦⎤
令
V
0
=
[
1
3
1
3
1
3
]
\mathbf V_0=\begin{bmatrix}\frac{1}{3}\\\frac{1}{3}\\\frac{1}{3}\end{bmatrix}
V0=⎣⎡313131⎦⎤
>> M=[0,0,0;0.5,0,0;0.5,1,0]
M =
0 0 0
0.5000 0 0
0.5000 1.0000 0
>> V0=[1/3,1/3,1/3]'
V0 =
0.3333
0.3333
0.3333
>> V1=M*V0
V1 =
0
0.1667
0.5000
>> V2=M*V1
V2 =
0
0
0.1667
>> V3=M*V2
V3 =
0
0
0
结果迭代到第三次时就已经得到全空的PR特征向量了
如何解决这种情况呢?
我们引入假设:没有指向任何网站的网站就相当于指向了任何网站
怎么理解这个假设呢?
用户在浏览完一个没有任何指向的网站时要继续浏览,肯定是关闭当前网站,重新打开一个网站,这个新打开的网站我们认为可能是n个网站中的任意一个
那么就相当于从这个没有出度的结点发出n-1条有向边指向其他n-1个结点
修正之后的M矩阵为:
M
=
[
0
0
1
3
1
2
0
1
3
1
2
1
1
3
]
\mathbf M=\begin{bmatrix} 0\ 0\ \frac{1}{3}\\ \frac{1}{2}\ 0\ \frac{1}{3}\\ \frac{1}{2}\ 1\ \frac{1}{3} \end{bmatrix}
M=⎣⎡0 0 3121 0 3121 1 31⎦⎤
>> M=[0,0,1/3;1/2,0,1/3;1/2,1,1/3]
M =
0 0 0.3333
0.5000 0 0.3333
0.5000 1.0000 0.3333
>> V0=[1/3 1/3 1/3]'
V0 =
0.3333
0.3333
0.3333
>> V100=M^100*V0
V100 =
0.1818
0.2727
0.5455
>> V200=M^200*V0
V200 =
0.1818
0.2727
0.5455
由此可见1迭代的结果是收敛的,
V → [ 0.1818 0.2727 0.5455 ] \mathbf V\rightarrow \begin{bmatrix} 0.1818\\0.2727\\0.5455\end{bmatrix} V→⎣⎡0.18180.27270.5455⎦⎤
修正算法:
引入标记函数
f
(
u
i
)
=
{
0
,
O
(
u
i
)
>
0
1
,
O
(
u
i
)
=
0
f(u_i)=\begin{cases}0,O(u_i)>0\\1,O(u_i)=0\end{cases}
f(ui)={0,O(ui)>01,O(ui)=0
M
1
=
M
+
o
n
e
s
(
n
,
n
)
d
i
a
g
(
f
1
,
f
2
,
.
.
.
,
f
n
)
n
\mathbf M_1=\mathbf M+\frac{ones(n,n)diag(f_1,f_2,...,f_n)}{n}
M1=M+nones(n,n)diag(f1,f2,...,fn)
其中
o
n
e
s
(
n
,
n
)
ones(n,n)
ones(n,n)表示n行n列,元素全是1的矩阵
d i a g ( f 1 , f 2 , . . . , f n ) diag(f_1,f_2,...,f_n) diag(f1,f2,...,fn)表示主对角线是标记函数,其余元素均为0的对角矩阵
spider traps问题及修正
有时某个网站存在自己指向自己的边,即在有向图上存在自回路
例如:
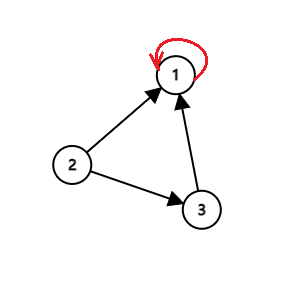
观察得出
M
=
[
1
1
2
1
0
0
0
0
1
2
0
]
\mathbf M=\begin{bmatrix} 1\ \frac{1}{2}\ 1\\ 0\ 0\ 0\\ 0\ \frac{1}{2}\ 0\\ \end{bmatrix}
M=⎣⎡1 21 10 0 00 21 0⎦⎤
由于所有结点都有出边,因此dead ends修正之后M不变
>> M=[1,0.5,1;0,0,0;0,0.5,0]
M =
1.0000 0.5000 1.0000
0 0 0
0 0.5000 0
>> V0=[1/3,1/3,1/3]'
V0 =
0.3333
0.3333
0.3333
>> V1=M*V0
V1 =
0.8333
0
0.1667
>> V2=M*V1
V2 =
1.0000
0
0
>> V3=M*V2
V3 =
1.0000
0
0
发现经过迭代,PR值都集中到这个有自回路的1号结点身上,2号和3号的PR值同为0,但是显然2号和3号的地位是不相同的
这种集中的原因是,1号结点是个貔貅一样的存在,自己手里的PR值不会外放,但是别人给的PR值照收不误,又每次迭代其他节点总是按照固定比例向1贡献自己的PR值,若干次迭代之后其他结点的PR值将会以无穷递缩等比数列削减,最终一定会全部汇集到这个1号点
如何解决这种情况呢?
我们需要想办法让用户不要老是呆在1号网站,要让他讨厌这个网站并转而浏览其他网站
引入假设:用户并不会老老实实地跟随网站上存在的链接访问其他网站,而是在每个页面上都有一定的概率,随机跳到任意一个网站.
怎么理解呢?我为了查matlab有没有网络流的函数,先到matlab帮助检索框检索网络流,打开第一个推荐的链接,里面提到了有向图digraph,恰好我不会,于是我需要学习digraph,于是点进了这个链接,那么如何创建一个digraph图呢?需要了解它的构造函数调用格式,于是又点进了它的一个构造函数的链接,这时候我不耐烦了,不想学了,我直接关了matlab的所有网页打开了B站…
修正算法:
假设
β
\beta
β是用户跟随出链继续访问下一个网站的概率,
1
−
β
1-\beta
1−β为用户不跟随出链访问下一个网站,转而访问随机网页(共有n个网页,这n个网页均摊概率)的概率
那么当前页面的PR值有两个去向和两个来源
去向1:跟随出链转移到后继结点
去向2:不跟随出链转移到任意结点
来源1:前驱结点根据出链转移到当前结点
来源2:任意结点不跟随出链转移到当前结点
P R ( u i ) = β ∑ j = 1 n g j i P R u j O ( u j ) + ( 1 − β ) ∑ j = 1 n P R ( u j ) n = { β [ g 1 i O ( u 1 ) g 2 i O ( u 2 ) . . . g n i O ( u n ) ] + ( 1 − β ) [ 1 n 1 n . . . 1 n ] } [ P R ( u 1 ) P R ( u 2 ) . . . P R ( u n ) ] = { β [ g 1 i g 2 i . . . g n i ] Λ + 1 − β n [ 1 1 . . . 1 ] } V \begin{aligned} PR(u_i)&=\beta\sum_{j=1}^n\frac{g_{ji}PR_{u_j}}{O(u_j)}+(1-\beta)\frac{\sum_{j=1}^nPR(u_j)}{n}\\ &=\{\beta[\frac{g_{1i}}{O(u_1)}\ \frac{g_{2i}}{O(u_2)}\ ...\ \frac{g_{ni}}{O(u_n)}]+(1-\beta)[\frac{1}{n}\ \frac{1}{n}\ ...\ \frac{1}{n}]\} \begin{bmatrix} PR(u_1)\\ PR(u_2)\\ ...\\ PR(u_n) \end{bmatrix}\\ &=\{\beta[g_{1i}\ g_{2i}\ ...\ g_{ni}]\Lambda+\frac{1-\beta}{n}[1\ 1\ ...\ 1]\}\mathbf V \end{aligned} PR(ui)=βj=1∑nO(uj)gjiPRuj+(1−β)n∑j=1nPR(uj)={β[O(u1)g1i O(u2)g2i ... O(un)gni]+(1−β)[n1 n1 ... n1]}⎣⎢⎢⎡PR(u1)PR(u2)...PR(un)⎦⎥⎥⎤={β[g1i g2i ... gni]Λ+n1−β[1 1 ... 1]}V
V k = { β G T Λ + 1 − β n o n e s ( n , n ) } V k − 1 \mathbf V_{k}=\{{\beta \mathbf G^T\Lambda}+\frac{1-\beta}{n}ones(n,n)\}\mathbf V_{k-1} Vk={βGTΛ+n1−βones(n,n)}Vk−1
故修正后的
M
M
M为
M
=
β
G
T
Λ
+
1
−
β
n
o
n
e
s
(
n
,
n
)
=
β
M
0
+
1
−
β
n
o
n
e
s
(
n
,
n
)
\mathbf M={\beta \mathbf G^T\Lambda}+\frac{1-\beta}{n}ones(n,n)\\ =\beta \mathbf M_0+\frac{1-\beta}{n}ones(n,n)
M=βGTΛ+n1−βones(n,n)=βM0+n1−βones(n,n)
如果考虑dead ends修正则此处
M
1
M_1
M1应为dead ends修正之后的矩阵
M
1
=
M
0
+
o
n
e
s
(
n
,
n
)
d
i
a
g
(
f
1
,
f
2
,
.
.
.
,
f
n
)
n
\mathbf M_1=\mathbf M_0+\frac{ones(n,n)diag(f_1,f_2,...,f_n)}{n}
M1=M0+nones(n,n)diag(f1,f2,...,fn)
M = β M 1 + 1 − β n o n e s ( n , n ) \mathbf M=\beta \mathbf M_1+\frac{1-\beta}{n}ones(n,n) M=βM1+n1−βones(n,n)
>> M0=[1,0.5,1;0,0,0;0,0.5,0]
M0 =
1.0000 0.5000 1.0000
0 0 0
0 0.5000 0
>> b=0.85
b =
0.8500
>> E=ones(3,3).*((1-b)/3)
E =
0.0500 0.0500 0.0500
0.0500 0.0500 0.0500
0.0500 0.0500 0.0500
>> M=M0.*b+E
M =
0.9000 0.4750 0.9000
0.0500 0.0500 0.0500
0.0500 0.4750 0.0500
>> V0=[1/3,1/3,1/3]'
V0 =
0.3333
0.3333
0.3333
>> V1=M*V0
V1 =
0.7583
0.0500
0.1917
>> V100=M^100*V0
V100 =
0.8788
0.0500
0.0713
>> V200=M^200*V0
V200 =
0.8788
0.0500
0.0713
V → [ 0.8788 0.0500 0.0713 ] \mathbf V\rightarrow \begin{bmatrix} 0.8788\\ 0.0500\\ 0.0713\\ \end{bmatrix} V→⎣⎡0.87880.05000.0713⎦⎤
最终算法
M = β ( M 0 + o n e s ( n , n ) d i a g ( f 1 , f 2 , . . . , f n ) n ) + 1 − β n o n e s ( n , n ) V k = M k V 0 \mathbf M=\beta (\mathbf M_0+\frac{ones(n,n)diag(f_1,f_2,...,f_n)}{n})+\frac{1-\beta}{n}ones(n,n)\\ \mathbf V_k=M^kV_0 M=β(M0+nones(n,n)diag(f1,f2,...,fn))+n1−βones(n,n)Vk=MkV0
n n n结点个数
M 0 = G T Λ M_0=G^T\Lambda M0=GTΛ由数据计算得到
f i f_i fi为结点 u i u_i ui是否有出度的标记, f i = { 1 , u i 无 出 度 0 , u i 有 出 度 fi=\begin{cases}1,u_i无出度\\0,u_i有出度\end{cases} fi={1,ui无出度0,ui有出度
d i a g ( f 1 , f 2 , . . . , f n ) diag(f_1,f_2,...,f_n) diag(f1,f2,...,fn)表示主对角线为 f 1 , f 2 , . . . , f n f_1,f_2,...,f_n f1,f2,...,fn,其他元素全为0的方阵
β \beta β为跟随链接继续访问的概率,通常在 [ 0.8 , 0.9 ] [0.8,0.9] [0.8,0.9]之间,取值 0.85 0.85 0.85
o n e s ( n , n ) ones(n,n) ones(n,n)表示n行n列,元素全是1的矩阵
matlab给出的方法:
























 9738
9738











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










